Раздел 2: Решение задач оптимизации с ограничениями с помощью MATLAB
Перечень тем курсовых работ
Раздел 1: Интерполяция и аппроксимация средствами MATLAB при решении инженерных задач
Задание 1. Нередко исходную информацию инженер может получить только в графическом виде. Чтобы пользоваться этой информацией в процессе проектирования с помощью ЭВМ, ее необходимо аппроксимировать аналитической зависимостью. На рисунке 1, кривая зависимости безразмерной величины нагрузки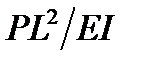 
от безразмерной деформации 
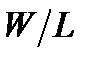Определить по этой кривой значения 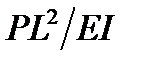при α=90° (для оцифровки графиков удобно воспользоваться программой GetData), соответствующие
W/L= -0,l; -0,2; -0,3; -0,4; -0,5; -0,6; -0,7; -0,8.
В пакете MATLAB c помощью метода наименьших квадратов аппроксимировать эти точки многочленами степеней 3, 5 и 7. Рассчитать для каждого аппроксимирующего многочлена погрешность, и проанализировать какая аппроксимация лучше.
Найти приближенные значения первой производной для точек, определенных по кривой. Полученные результаты сравнить с производными многочленов, найденных методом наименьших квадратов.
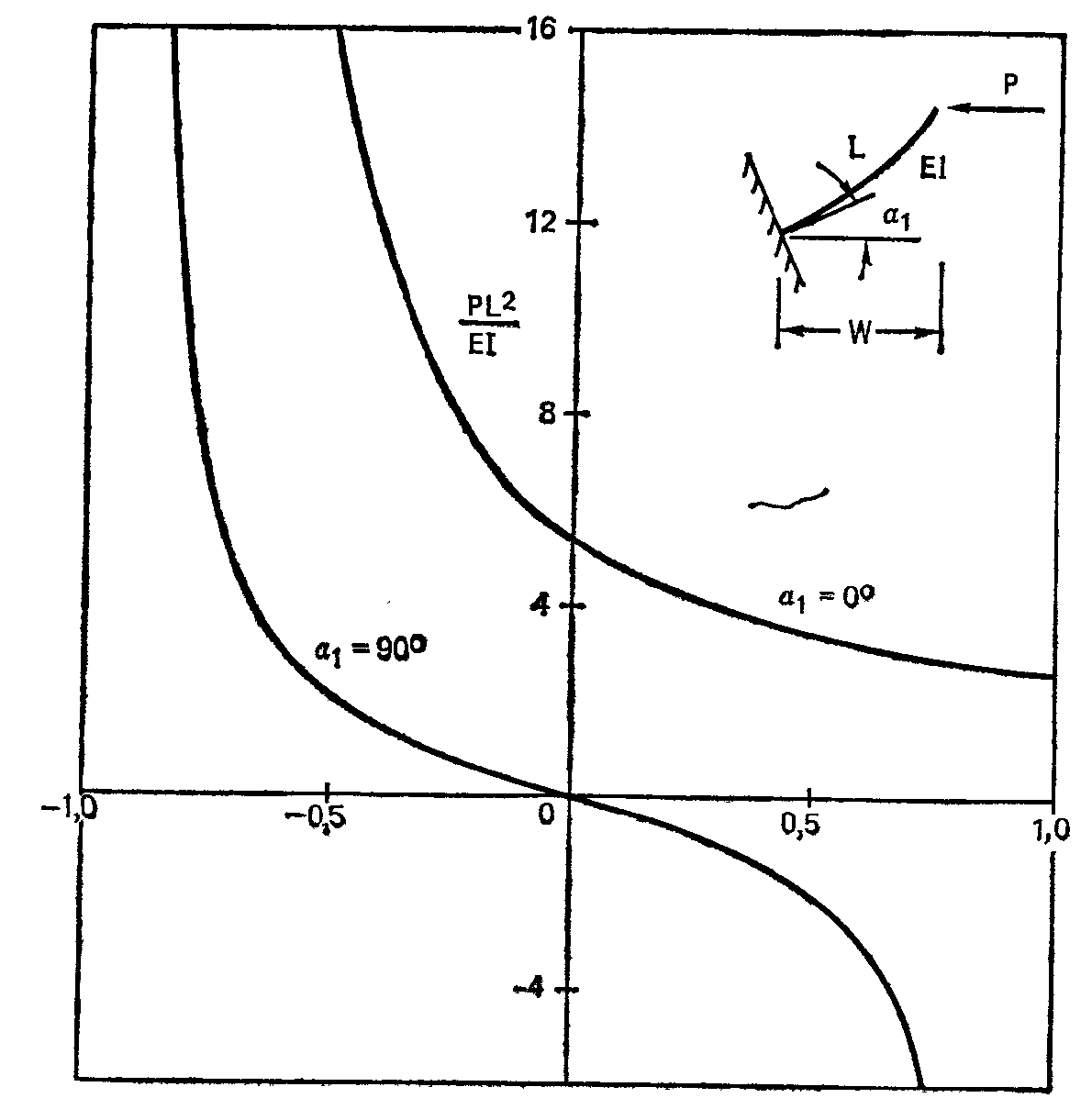
Рисунок 1 – Кривая зависимости безразмерной величины нагрузки 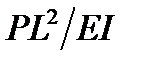от безразмерной деформации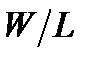
Задание 2. Определить по кривой (рисунок 1), при α=0° (для оцифровки графиков удобно воспользоваться программой GetData) значение 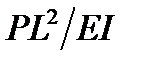в интервале 
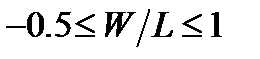, и интерполировать полученные данные с помощью кусочно-линейной интерполяцией и кубическим сплайном. Результаты интерполяции представить графически. Определить площадь под кривой численным интегрированием.
Задание 3. В таблице 1, приведены средние значения роста лиц мужского пола в возрасте от 4 до 17 лет. Для аппроксимации этих данных Берталаифи (von Bertalanffy L., Quantitative Laws in Metabolism and Growth, Quarterly Review of Biology, 82, pp. 217–231, 1957) предложил формулу
.
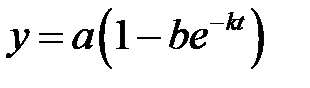где a, b и k – постоянные величины, которые требуется определить. Найти наилучшие значения этих постоянных методом наименьших квадратов. Определить и представить графически скорость роста лиц мужского пола. В каком возрасте она максимальна?
Таблица 1
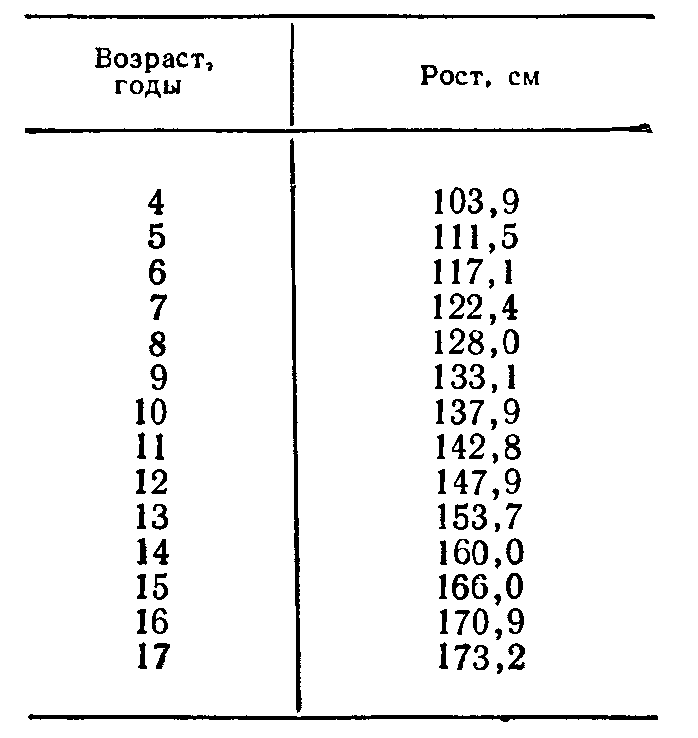
Раздел 2: Решение задач оптимизации с ограничениями с помощью MATLAB
Задание 4. Емкость резервуара для жидких отходов должна составлять 40 000 л. Изготовляется резервуар из железобетона толщиной 10 см. С помощью функций пакета MATLAB определить геометрические параметры резервуара, при которых на его изготовление пойдет минимальное количество бетона.
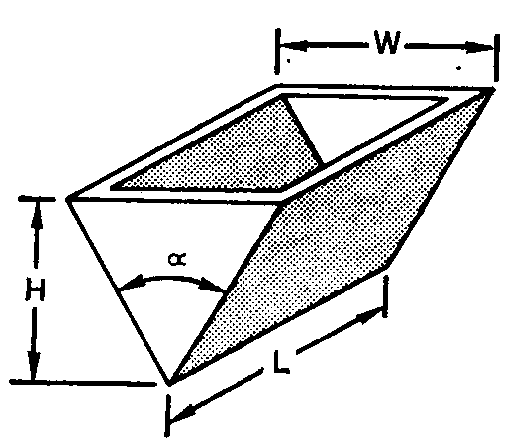
Задание 5. Изготовитель контейнеров проектирует открытый контейнер из листового материала, раскрой которого показан на рисунке. Заготовка вырезается из листа, сгибается по пунктирным линиям и сваривается четырьмя швами. Определить с использованием средств MATLAB, каковы должны быть размеры контейнера наибольшего объема, если площадь его дна не должна превышать 1 м2 и ни одни из линейных размеров a, b и c не должен быть больше другого более чем в 3 раза.
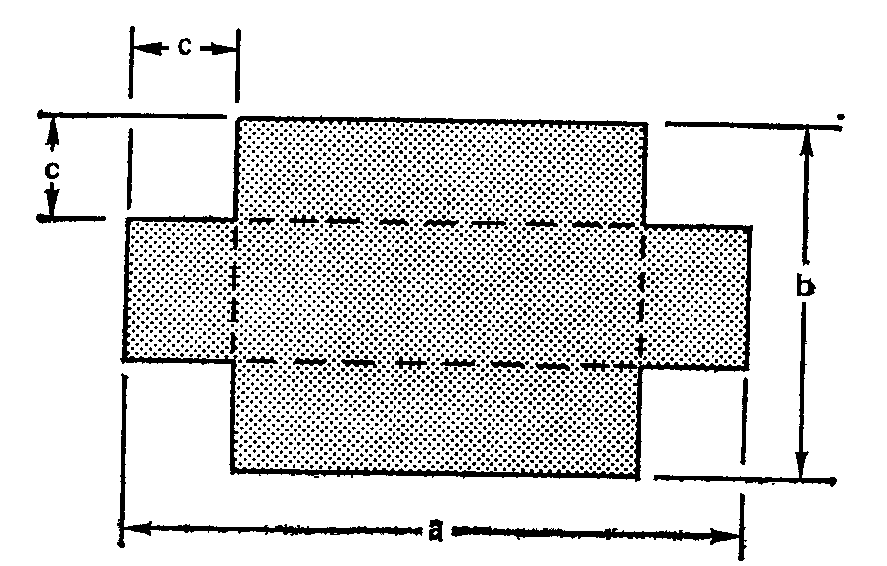
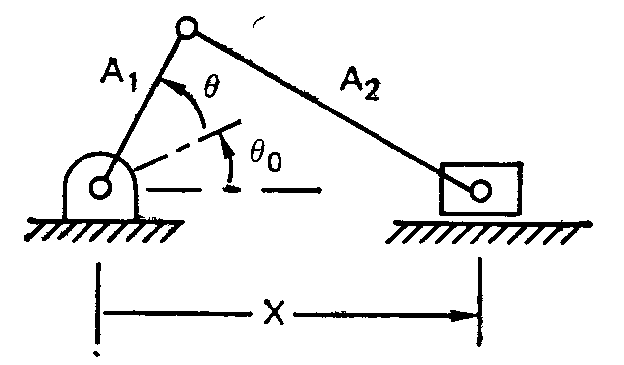
Задание 6. С использованием MATLAB осуществить выбор геометрических параметров кривошипно-шатунного механизма, показанного на рисунке, так чтобы достигнуть наилучшей аппроксимации (с наименьшей ошибкой) с помощью формулы:
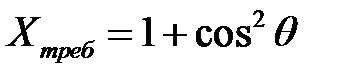при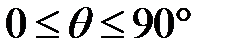 
Действительная зависимость x(θ) выражается соотношением:
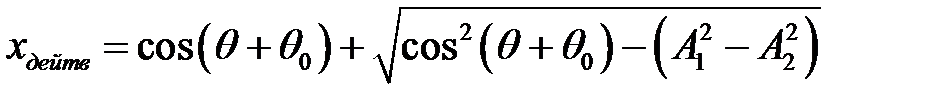
Ошибку можно выразить в виде
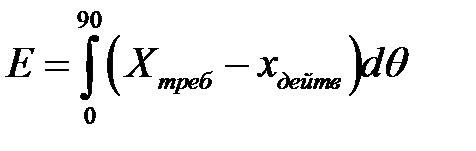
Дополнительные условия имеют вид
; 
; 
.
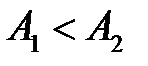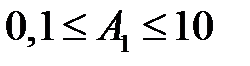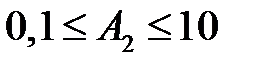Задание 7. Передаточное отношение зубчатой передачи, показанной на рисунке, связывающее угловую скорость последней шестерни с угловой скоростью первой i, зависит от числа зубьев Nj каждой шестерни:
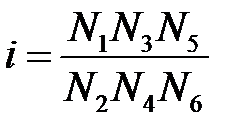
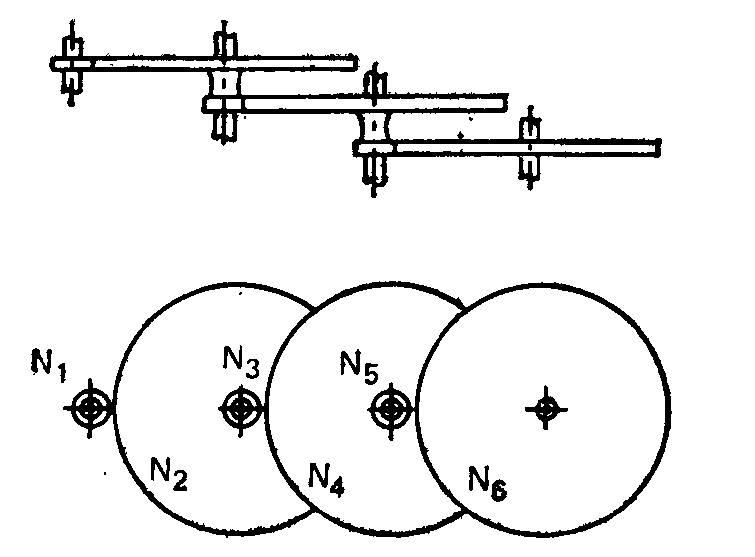
Требуется с помощью MATLAB спроектировать зубчатую передачу, для которой i было бы как можно ближе к 1/10π. По практическим соображениям число зубьев Nj должно быть заключено в интервале значений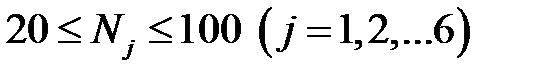 
. Выбрать наилучшую возможную конструкцию, найдя значения Nj.
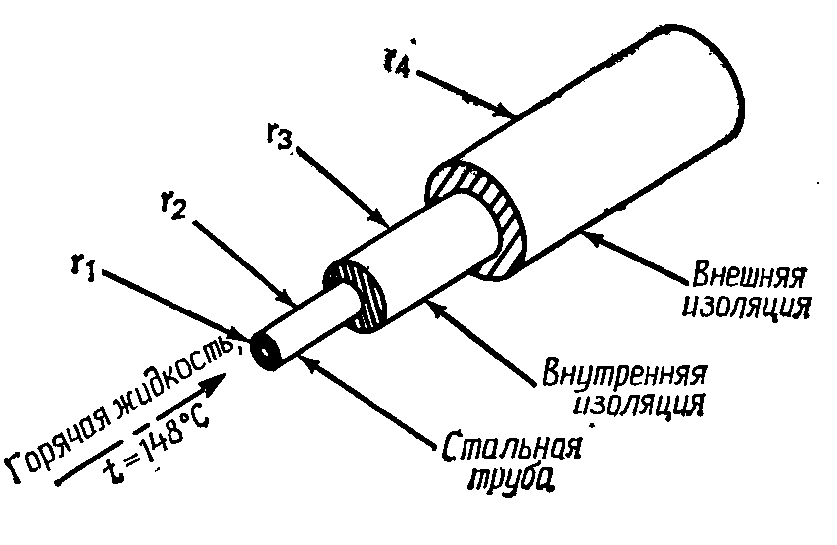
Задание 8. По стальной трубе внешним диаметром 8,9 см и внутренним диаметром 7,8 см (коэффициент теплопроводности k=43,27 Вт/(м∙К)) подается нагретая жидкость при температуре 148 °С. Труба имеет два слоя изоляции. Коэффициент теплопроводности внутреннего слоя изоляции k=0,2 Вт/(м∙К), внешнего – k=0,5 Вт/(м∙К). Коэффициент теплоотдачи на внутренней поверхности трубы 230 Вт/(м2∙К), а на внешней поверхности изоляции 23 Вт/(м2∙К). Максимальная допустимая температура внешней поверхности изоляции 38 °С, температура окружающего воздуха 27 °С. Требуется так спроектировать изоляцию трубы, чтобы ее стоимость была минимальной. Максимальный допустимый внешний радиус 12 см, стоимость материала внутреннего слоя изоляции 35 долл./м3, а материала внешнего слоя 100 долл./м3. Теплообменом между слоями изоляции можно пренебречь.
