Решение задач оптимизации конструкции с помощью изобретательских стандартов
Известные типы изобретательских задач решаются использованием, прежде всего типовых решений - стандартов на решение изобретательских задач. Они представляют собой взаимосвязанный комплекс приемов, физических или других эффектов, имеющих определенную вепольную структуру. Это своего рода формулы, по которым решаются задачи.
Современная система написана на языке вещественно-полевых преобразований и включает 76 стандартов. Все стандарты сгруппированы в 5 классов.
1 класс содержит правила достройки и разрушения веполей.
2 класс показывает, как повысить эффективность работы веполя путем небольших изменений.
3 класс дает рекомендации на повышение эффективности и управляемости вепольных моделей с использованием ЗРТС (законы развития технических систем).
4 класс предназначен для решения задач на обнаружение и измерение.
5 класс содержит проверенные рекомендации по применению самих стандартов.
Любую задачу можно решить на разных уровнях – от 1 до 5. Стандартное решение – это одно из возможных решений.
Пример стандарта 1-го класса:
1.1.1. Синтез веполя
Если дан объект, плохо поддающийся нужным изменениям, и условия не содержат ограничений на введение веществ и полей, задачу решают синтезом веполя, вводя недостающие элементы.
Конец примера.
19) Понятие мат. планирования. ПФЭ2n для двухфакторной модели. Вычисление коэффициентов регрессии.
При мат. Планировании экспериментов исследуются экспериментально формальные связи входных и выходных параметров. Ключевая цель: установление зависимостей, связывающих входные и выходные параметры. Полученные связи и есть формализованная математическая модель системы. Исследование такой модели приводит к формулированию оптимальных условий ведения процесса. Исследовать влияние входных параметров на выходные можно методом пассивного эксперимента (за счет случайного изменения входных параметров) и активного (значения входных данных изменяются по заранее составленному плану).
Преимущества исследований с применением математических методов состоят в огромном сокращении времени и затрат и большей вероятности достичь действительного экстремума. Большинство математических методов планирования экстремальных экспериментов (поиск минимального или максимального, повышение производительности – max, снижение себестоимости - min) значения дает возможность по результатам экспериментов составить математическое описание процесса в виде уравнения регрессии.
В этом случае планирование эксперимента и его осуществление распадается на следующие этапы. 1. Высказывается гипотеза о возможности описания процесса уравнением регрессии (степенным рядом определенного порядка).
2. В соответствии с этой гипотезой планируется и осуществляется эксперимент.
3. По результатам эксперимента рассчитываются коэффициенты регрессии и составляется математическое описание в соответствии с первоначальной гипотезой.
4. Проводится статистическая оценка значимости коэффициентов уравнения регрессии.
5. Осуществляется статистический анализ адекватности (соответствия) полученного уравнения действительному течению процесса, проверяется первоначальная гипотеза, а также гипотезы, максимально упрощающие уравнения при сохранении ее адекватности изучаемому процессу.
6. Используя полученное уравнение, тем или иным методом решается вопрос об определении оптимальных условий протекания исследуемого процесса.
В планах ПФЭ2n «n» факторов во всевозможных сочетаниях друг с другом на двух уровнях дают условия постановки единичных опытов в рамках предпринятого экспериментального исследования.
Размеры матрицы планирования 2-факторного эксперимента определяются по 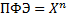
где X – наивысший порядок для нахождения любого из переменных факторов функции отклика, ед., n- количество переменных факторов, ед.
Для 2 факторного эксперимента число столбцов соответствует числу переменных факторов, т.е. 2. А число строк зависит от Х, т.е. это и есть 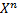 .
.
| Номер опыта | С1 | С2 | уu |
| 1 опыт |  |  | у1 |
| 2 опыт | 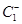 | 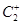 | у2 |
| 3 опыт | 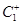 | 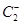 | у3 |
| 4 опыт | 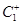 | 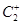 | у4 |
И т.д….
Вычисление коэффициентов регрессии. Уравнение регрессии - математическое описание процесса в общем виде, представленное зависимостью определенного порядка Y=f(x1.x2…xn). Вид этой функции неизвестен, но в любом случае она может быть представлена бесконечным степенным рядом.
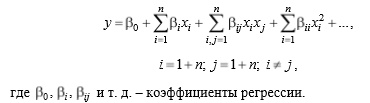
Уравнение регрессии представляют собой геометрическое уравнение гиперповерхности в (n + 1)-мерном факторном пространстве. Эта гиперповерхность называется поверхностью отклика. Изучение формы поверхности отклика, нахождение оптимальных значений исследуемых параметров является сущностью рассматриваемых методов планирования эксперимента.
· Если проводится однофакторный эксперимент, то поверхность отклика сжимается в линию на плоскости.
· При n = 2 поверхность отклика будет располагаться в трехмерном факторном пространстве.
· При n = 3 поверхность отклика лежит в четырехмерном пространстве. Изобразить эту поверхность невозможно. Графически изобразить поверхность отклика при n>3 не представляется возможным.


20) Понятие мат. планирования. ПФЭ2n для трёххфакторной модели. Вычисление коэффициентов регрессии.
При мат. Планировании экспериментов исследуются экспериментально формальные связи входных и выходных параметров. Ключевая цель: установление зависимостей, связывающих входные и выходные параметры. Полученные связи и есть формализованная математическая модель системы. Исследование такой модели приводит к формулированию оптимальных условий ведения процесса. Исследовать влияние входных параметров на выходные можно методом пассивного эксперимента (за счет случайного изменения входных параметров) и активного (значения входных данных изменяются по заранее составленному плану).
Преимущества исследований с применением математических методов состоят в огромном сокращении времени и затрат и большей вероятности достичь действительного экстремума. Большинство математических методов планирования экстремальных экспериментов (поиск минимального или максимального, повышение производительности – max, снижение себестоимости - min) значения дает возможность по результатам экспериментов составить математическое описание процесса в виде уравнения регрессии.
В этом случае планирование эксперимента и его осуществление распадается на следующие этапы. 1. Высказывается гипотеза о возможности описания процесса уравнением регрессии (степенным рядом определенного порядка).
2. В соответствии с этой гипотезой планируется и осуществляется эксперимент.
3. По результатам эксперимента рассчитываются коэффициенты регрессии и составляется математическое описание в соответствии с первоначальной гипотезой.
4. Проводится статистическая оценка значимости коэффициентов уравнения регрессии.
5. Осуществляется статистический анализ адекватности (соответствия) полученного уравнения действительному течению процесса, проверяется первоначальная гипотеза, а также гипотезы, максимально упрощающие уравнения при сохранении ее адекватности изучаемому процессу.
6. Используя полученное уравнение, тем или иным методом решается вопрос об определении оптимальных условий протекания исследуемого процесса.
В планах ПФЭ2n «n» факторов во всевозможных сочетаниях друг с другом на двух уровнях дают условия постановки единичных опытов в рамках предпринятого экспериментального исследования.
Размеры матрицы планирования 3-факторного эксперимента определяются по 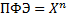
где X – наивысший порядок для нахождения любого из переменных факторов функции отклика, ед., n- количество переменных факторов, ед.
Для 3-факторного эксперимента число столбцов соответствует числу переменных факторов, т.е. 3. А число строк зависит от Х, т.е. это и есть 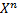 .
.
Таблица 3.3.Матрица плана ПФЭ23
| U | x1 | x2 | x3 | yu |
| - | - | - | y1 | |
| - | + | - | y2 | |
| + | - | - | y3 | |
| + | + | - | y4 | |
| - | - | + | y5 | |
| - | + | + | y6 | |
| + | - | + | y7 | |
| + | + | + | y8 |
Для этого удваивают матрицу двухфакторного эксперимента, первые 4
из 8 полученных опытов проводят при нижнем уровне третьего фактора, остальные 4 – при верхнем.
Вычисление коэффициентов регрессии. Уравнение регрессии - математическое описание процесса в общем виде, представленное зависимостью определенного порядка Y=f(x1.x2…xn). Вид этой функции неизвестен, но в любом случае она может быть представлена бесконечным степенным рядом.
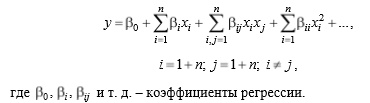
Уравнение регрессии представляют собой геометрическое уравнение гиперповерхности в (n + 1)-мерном факторном пространстве. Эта гиперповерхность называется поверхностью отклика. Изучение формы поверхности отклика, нахождение оптимальных значений исследуемых параметров является сущностью рассматриваемых методов планирования эксперимента.
· Если проводится однофакторный эксперимент, то поверхность отклика сжимается в линию на плоскости.
· При n = 2 поверхность отклика будет располагаться в трехмерном факторном пространстве.
· При n = 3 поверхность отклика лежит в четырехмерном пространстве. Изобразить эту поверхность невозможно. Графически изобразить поверхность отклика при n>3 не представляется возможным.
План ПФЭ23 – трехфакторного эксперимента получают из плана ПФЭ22.
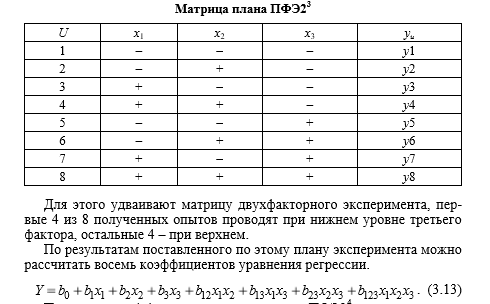
23. Понятие планирования эксперимента ПФЭ 3n для 2-х факторной модели. Вычисление коэффициентов регрессии.
В общем случае эксперимент, в котором реализуются все возможные сочетания уровней факторов, называется полным факторным экспериментом.
Если выбранная модель включает нелинейные члены полинома и их произведения, то для оценки всех параметров модели используется план эксперимента с варьированием всех факторов на трех уровнях. Такие планы принято называть планами типа 3n, где 3n=N – число всех возможных опытов, n – количество варьируемых факторов.
Полный факторный эксперимент может быть предложен исследователю как один из способов построения математической модели (идентификации) недетерминированного объекта. Этот способ оказывается наиболее предпочтительным в тех случаях, когда отсутствует априорная информация для обоснования структуры модели с позиций физико-химических представлений процессов, происходящих в объекте, отсутствует количественная оценка степени влияния изучаемых факторов на выходную переменную объекта, его выходной показатель.
Теорию и планы полного факторного эксперимента разработал в тридцатые годы двадцатого века Р.Фишер. С этих работ и начинают развиваться теория и практика математических методов планирования экстремальных экспериментов.
В планах ПФЭ2n «n» факторов во всевозможных сочетаниях друг с другом на двух уровнях дают условия постановки единичных опытов в рамках предпринятого экспериментального исследования.
Число таких единичных опытов, соответствующее числу возможных комбинаций всех факторов на двух уровнях, равно N = 2n.
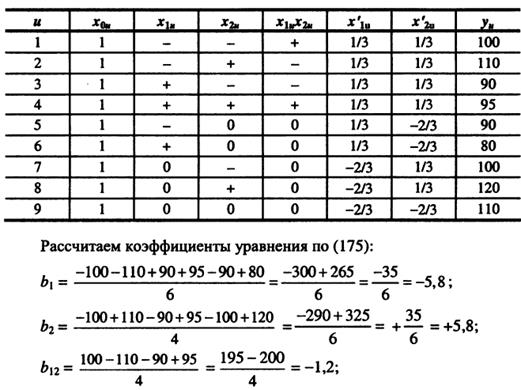
Таблица 3.4.План ПФЭ32
| U | x1 | x2 | X’1 | X'2 | Х1X2 |
| − | − | 1/3 | 1/3 | + | |
| − | + | 1/3 | 1/3 | − | |
| + | − | 1/3 | 1/3 | − | |
| + | + | 1/3 | 1/3 | + | |
| - | 1/3 | -2/3 | |||
| + | 1/3 | -2/3 | |||
| - | -2/3 | 1/3 | |||
| + | -2/3 | 1/3 | |||
| -2/3 | -2/3 |


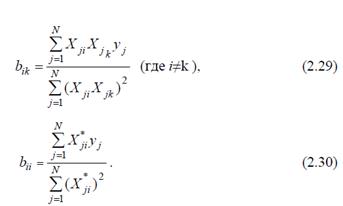

24. Понятие планирования эксперимента ПФЭ 3n для 3-х факторной модели. Вычисление коэффициентов регрессии.
В общем случае эксперимент, в котором реализуются все возможные сочетания уровней факторов, называется полным факторным экспериментом.
Если выбранная модель включает нелинейные члены полинома и их произведения, то для оценки всех параметров модели используется план эксперимента с варьированием всех факторов на трех уровнях. Такие планы принято называть планами типа 3n, где 3n=N – число всех возможных опытов, n – количество варьируемых факторов.
Полный факторный эксперимент может быть предложен исследователю как один из способов построения математической модели (идентификации) недетерминированного объекта. Этот способ оказывается наиболее предпочтительным в тех случаях, когда отсутствует априорная информация для обоснования структуры модели с позиций физико-химических представлений процессов, происходящих в объекте, отсутствует количественная оценка степени влияния изучаемых факторов на выходную переменную объекта, его выходной показатель.
Теорию и планы полного факторного эксперимента разработал в трид-цатые годы двадцатого века Р.Фишер. С этих работ и начинают развиваться теория и практика математических методов планирования экстремальных экспериментов.
В планах ПФЭ2n «n» факторов во всевозможных сочетаниях друг с дру-гом на двух уровнях дают условия постановки единичных опытов в рамках предпринятого экспериментального исследования.
Число таких единичных опытов, соответствующее числу возможных комбинаций всех факторов на двух уровнях, равно N = 2n.
Таблица 3.4.План ПФЭ33
| U | x1 | x2 | X3 | X’1 | X'2 | X'3 | Х1X2 | Х2X3 | Х1X3 |
| - | - | - | 1/3 | 1/3 | 1/3 | + | + | + | |
| + | - | - | 1/3 | 1/3 | 1/3 | - | + | - | |
| + | + | - | 1/3 | 1/3 | 1/3 | + | - | - | |
| - | - | + | 1/3 | 1/3 | 1/3 | + | - | - | |
| + | - | + | 1/3 | 1/3 | 1/3 | - | - | + | |
| - | - | 1/3 | 1/3 | -2/3 | + | ||||
| - | + | 1/3 | 1/3 | -2/3 | - | ||||
| + | - | 1/3 | 1/3 | -2/3 | - | ||||
| + | + | 1/3 | 1/3 | -2/3 | + | ||||
| + | - | 1/3 | -2/3 | 1/3 | - | ||||
| - | - | -2/3 | 1/3 | 1/3 | + | ||||
| - | -2/3 | -2/3 | 1/3 | ||||||
| + | + | 1/3 | -2/3 | 1/3 | + | ||||
| + | + | -2/3 | 1/3 | 1/3 | + | ||||
| + | -2/3 | -2/3 | 1/3 | ||||||
| - | 1/3 | -2/3 | -2/3 | ||||||
| - | -2/3 | 1/3 | -2/3 | ||||||
| + | -2/3 | 1/3 | -2/3 | ||||||
| -2/3 | -2/3 | -2/3 | |||||||
| - | + | - | 1/3 | 1/3 | 1/3 | - | - | + | |
| + | + | + | 1/3 | 1/3 | 1/3 | + | + | + | |
| - | - | 1/3 | -2/3 | 1/3 | + | ||||
| - | + | 1/3 | -2/3 | 1/3 | - | ||||
| + | 1/3 | -2/3 | -2/3 | ||||||
| + | - | -2/3 | 1/3 | 1/3 | - | ||||
| - | + | -2/3 | 1/3 | 1/3 | - | ||||
| - | + | + | 1/3 | 1/3 | 1/3 | - | + | - |


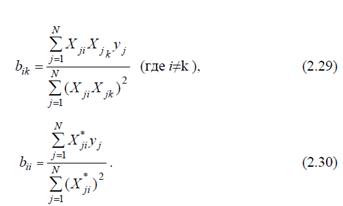
25. Понятие планирования эксперимента ПФЭ 3n для 3-х факторной модели. Вычисление коэффициентов регрессии.
План полного 4-х факторного эксперимента ПФЭ24 получают тем же методом из плана ПФЭ22 (табл.3.4).
Таблица 3.4.План ПФЭ24
| U | x1 | x2 | x3 | х4 | |
| - | - | - | - | «1» | |
| - | + | - | - | x2 | |
| + | - | - | - | x1 | |
| + | + | - | - | x1x2 | |
| - | - | + | - | х3 | |
| - | + | + | - | х2x3 | |
| + | - | + | - | x1x3 | |
| + | + | + | - | х1x2х3 | |
| - | - | - | + | х4 | |
| - | + | - | + | х2x4 | |
| + | - | - | + | x1x4 | |
| + | + | - | + | х1x2х4 | |
| - | - | + | + | х3x4 | |
| - | + | + | + | х2x3х4 | |
| + | - | + | + | х1x3х4 | |
| + | + | + | + | х1x2х3х4 |
Дополнительный столбец является другой формой записи плана эксперимента – в соответствующей строке выписываются в качестве сомножителей факторы, находящиеся на верхнем уровне. Остальные факторы на нижнем уровне.
Разрешающая способность плана ПФЭ24 – 16 коэффициентов уравнения регрессии:
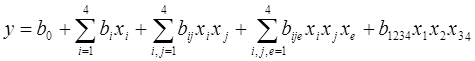 (3.14)
(3.14)
Как увидим несколько позже, число коэффициентов должно быть несколько меньше, в противном случае становится невозможным статистический анализ адекватности уравнения регрессии.
Учитывая уравнение (5.10) и план ПФЭ можно построить формулы для определения коэффициентов уравнения:
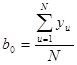 ;
; 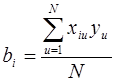 ;
; 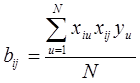 . (3.12)
. (3.12)
В этих формулах
u – номер варианта опыта;
i – номер фактора;
j – номер фактора отличный от i.
26. Понятие математической модели ДФЭ 2n – n’ для 3-х факторной модели. Вычисление коэффициентов регрессии.
С увеличением количества факторов резко возрастает количество опытов полного факторного эксперимента. Это видно из уравнения N=2n. Однако для нахождения коэффициентов регрессии не всегда требуется много опытов. В таких случаях можно уменьшить объем экспериментальных работ, воспользовавшись методом дробных реплик.
Рассматриваемый метод заключается в том, что для нахождения математического описания процесса используется определенная часть полного факторного эксперимента: 1/2, 1/4 и т. д. Эти системы опытов называются дробными репликами (табл. 2.4).
Таблица 2.4
Полный трехфакторный эксперимент и его дробные реплики
| Номер опыта | Факторы | Функция отклика | Дробные Реплики | ||
| X1 | x2 | x3 | |||
| −1 | −1 | −1 | y1 |   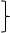 1/2 1/4 1/2 1/2 1/4 1/2 | |
| +1 | −1 | −1 | y2 | ||
| −1 | +1 | −1 | y3 | ||
| +1 | +1 | −1 | y4 | ||
| −1 | −1 | +1 | y5 | 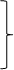 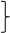 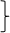 1/2 1/4 1/2 1/2 1/4 1/2 | |
| +1 | −1 | +1 | y6 | ||
| −1 | +1 | +1 | y7 | ||
| +1 | +1 | +1 | y8 |
Расчет коэффициентов регрессии, проверка значимости коэффициентов и адекватности математического описания в данном случае производятся так же, как и при полном факторном эксперименте.
Пусть, например, требуется найти коэффициенты уравнения регрессии
y = b0 + b1X1 + b2X2 + b3X3 .
Здесь четыре неизвестных коэффициента.
Если для их определения воспользоваться полным трехфакторным экспериментом, то необходимо провести 8 опытов. Однако эту задачу можно решить и с помощью меньшего количества опытов.
Например, возьмем матрицу полного двухфакторного эксперимента (табл.2.5)
и приравняем произведение X1X2 к фактору X3.
Пользуясь формулой (2.14), вычислим:
b0 =1/4( y1 + y2 + y3 + y4) ,
b1 = ¼(−y1 + y2 − y3 + y4) ,
b2 = ¼(−y1 − y2 + y3 + y4) .
Таблица 2.5
Планирование типа 23−1
| Номер опыта | Факторы | Функция отклика | ||
| X1 | x2 | x3 | ||
| −1 | −1 | +1 | y1 | |
| +1 | −1 | +1 | y2 | |
| −1 | +1 | −1 | y3 | |
| +1 | +1 | −1 | y4 |
Отметим, что в табл. 2.5 столбцы для произведения X1X2 и фактора X3 полностью совпадают. Поэтому коэффициенты b12 и b3 не могут быть определены раздельно. С помощью формулы (2.14) может быть найдена только их сумма:
b12 + b3 = ¼(y1 − y2 − y3 + y4) .
Этот недостаток рассматриваемого плана является своеобразной «платой» за уменьшение общего количества опытов с восьми до четырех.
Такое планирование эксперимента, когда некоторые из факторов приравнивают к произведениям нескольких факторов, называется планированием со смешиванием. Его обозначают символом 2n−p, где n – общее число факторов, а р – число
факторов, приравненных к произведениям. С этой точки зрения в табл. 2.5 приведена матрица планирования типа 23−1.
Существует правило, позволяющее определить, какие коэффициенты регрессии определяются совместно при планировании со смешиванием. Рассмотрим это правило на конкретном примере.
Пример. Методом дробных реплик будем искать математическое описание
процесса в виде уравнения регрессии:
y = b0 + b1X1 + b2X2 + B3X3 + b4X4 + b5X5 .
Воспользуемся планированием типа 25−2 и примем:
X4 = −X1X2 ;
X5 = X1X2X3 .
Такие равенства в методе дробных реплик называют генерирующими соотношениями.
Следует отметить, что выбор генерирующих соотношений в общем случае произволен. Однако он существенно влияет на характер совместных оценок коэффициентов регрессии.
Правило определения совместных оценок коэффициентов состоит в следующем.
1. Примем во внимание, что
Xi2 =1;
Xi ⋅1= Xi .
2. Умножив обе части генерирующих соотношений соответственно на X4 и X5,получим:
1= −X1X2X4 ;
1 = X1X2X3X5 .
Эти равенства называют определяющими контрастами. Перемножив их почленно, получим новые определяющие контрасты. В данном случае это
1= −X3X4X5 .
3. Составим алгебраическую сумму из единицы и правых частей всех полученных определяющих контрастов:
S =1− X1X2X4 + X1X2X3X5 − X3X4X5 .
4. Умножив каждый из факторов на S и заменив факторы соответствующими коэффициентами разложения в ряд Тейлора (2.5), получим:
b1→β1 −β24 + β235 −β1345 ;
b2 →β2 − β14 + β135 − β2345 ;
b3 →β3 −β1234 + β125 −β45 ;
b4 →β4 −β12 + β12345 −β35 ;
b5 →β5 −β1245 + β123 −β34 .
27. Понятие доверительной интервала плана эксперимента и использование при составлении математического плана эксперимента
28. Определение минимального необходимого числа повторностей опыта и влияние его на точность описания исследуемого процесса
29. Составление уравнения регрессиидля обработки результатов реализации планов ПФЭ 2n
Вычисление коэффициентов регрессии. Уравнение регрессии - математическое описание процесса в общем виде, представленное зависимостью определенного порядка Y=f(x1.x2…xn). Вид этой функции неизвестен, но в любом случае она может быть представлена бесконечным степенным рядом.
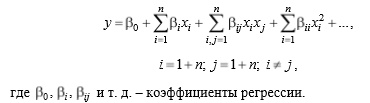
Уравнение регрессии представляют собой геометрическое уравнение гиперповерхности в (n + 1)-мерном факторном пространстве. Эта гиперповерхность называется поверхностью отклика. Изучение формы поверхности отклика, нахождение оптимальных значений исследуемых параметров является сущностью рассматриваемых методов планирования эксперимента.
· Если проводится однофакторный эксперимент, то поверхность отклика сжимается в линию на плоскости.
· При n = 2 поверхность отклика будет располагаться в трехмерном факторном пространстве.
· При n = 3 поверхность отклика лежит в четырехмерном пространстве. Изобразить эту поверхность невозможно. Графически изобразить поверхность отклика при n>3 не представляется возможным.
План ПФЭ23 – трехфакторного эксперимента получают из плана ПФЭ22.

30. Составление уравнения регрессиидля обработки результатов реализации планов ПФЭ 3n
31.Составление уравнения регрессии для обработки результатов для реализации планов ДФЭ 2n – n’
ответ в вопросе 26
32. Оптимальные планы поиск оптимального решения методом крутого восхождения к градиенту:
Метод крутого восхождения — математический метод планирования экспериментана стадии поиска экстремума функции отклика основан на шаговом движении в область оптимума по градиенту линейного приближения.
Использование метода крутого восхождения связано с некоторыми трудностями и ограничениями. Так. при использовании нескольких оценочных характеристик этот метод становится малоэффективным. Кроме того, относительно большой объем расчетов требует применения вычислительных машин. В таких случаях более приемлем метод симплексного планирования экспериментов.
Задача оптимизации, т. е. выбора режимов эксперимента, заключается в том, чтобы при минимальном числе опытов достигнуть оптимума, т. е. произвести так называемоекрутое восхождение . Наибольшее распространение при поиске оптимальных условийпроцесса получил метод факторного планирования. Он позволяет одновременно исследовать влияние на процесс u ex изучаемых параметров и представить результаты в виде уравпения. Рассмотрим принцип математического планирования па конкретном примере.
33.Оптимальные планы. Поиск оптимального решения методом симплекса.
Симплекс-метод - алгоритм решения оптимизационной задачи линейного программирования путём перебора вершин выпуклого многогранника в многомерном пространстве. Данный метод, имеющий несколько различных форм (модификаций), был разработан в 1947 году Г. Данцигом.
Задача линейного программирования состоит в том, что необходимо максимизировать или минимизировать некоторый линейный функционал на многомерном пространстве при заданных линейных ограничениях.
Заметим, что каждое из линейных неравенств на переменные ограничивает полупространство в соответствующем линейном пространстве. В результате все неравенства ограничивают некоторый многогранник (возможно, бесконечный), называемый также полиэдральным конусом. Уравнение W(x) = c, где W(x) — максимизируемый (или минимизируемый) линейный функционал, порождает гиперплоскость L(c). Зависимость от c порождает семейство параллельных гиперплоскостей. Тогда экстремальная задача приобретает следующую формулировку — требуется найти такое наибольшее c, что гиперплоскость L(c) пересекает многогранник хотя бы в одной точке. Заметим, что пересечение оптимальной гиперплоскости и многогранника будет содержать хотя бы одну вершину, причём, их будет более одной, если пересечение содержит ребро или k-мерную грань. Поэтому максимум функционала можно искать в вершинах многогранника.
Принцип симплекс-метода состоит в том, что выбирается одна из вершин многогранника, после чего начинается движение по его рёбрам от вершины к вершине в сторону увеличения значения функционала. Когда переход по ребру из текущей вершины в другую вершину с более высоким значением функционала невозможен, считается, что оптимальное значение c найдено.
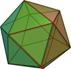
Многогранник ограничивающих условий для 3-мерного пространства
Рассмотрим теперь более подробно основы симплекс-метода и сформулируем алгоритм. Для решения системы все неизвестные произвольно подразделяют на базисные и свободные. Число базисных переменных определяется числом линейно-независимых уравнений. Остальные неизвестные свободные. Им придают произвольные значения и подставляют в систему. Любому набору свободных неизвестных можно придать бесчисленное множество произвольных значений, которые дадут бесчисленное множество решений. Если все свободные неизвестные приравнять к нулю, то решение будет состоять из значений базисных неизвестных. Такое решение называется базисным.
В теории линейного программирования существует теорема, которая утверждает, что среди базисных решений системы можно найти оптимальное, а в некоторых случаях и несколько оптимальных решений, но все они обеспечат экстремум целевой функции. Таким образом, если найти какой-либо базисный план, а затем улучшить его, то получится оптимальное решение. На этом принципе и построен симплекс-метод.
Последовательность вычислений симплекс-методом можно разделить на две основные фазы:
нахождение исходной вершины множества допустимых решений (нахождение базисного решения),
последовательный переход от одной вершины к другой, ведущий к оптимизации значения целевой функции (последовательное улучшение найденого на первом этапе базисного решения).
При этом в некоторых случаях исходное решение очевидно или его определение не требует сложных вычислений, например, когда все ограничения представлены неравенствами вида «меньше или равно» (тогда нулевой вектор совершенно точно является допустимым решением, хотя и, скорее всего, далеко не самым оптимальным). В таких задачах первую фазу симплекс-метода можно вообще не проводить. Симплекс-метод, соответственно, делится на однофазный и двухфазный.
Тонкости симплекс метода
1) Когда прямая (если рассматривается двухмерная задача линейного программирования, а в общем случае гиперплоскость), представляющая целевую функцию параллельна прямой (гиперплоскости), соответствующей одному из неравенств-ограничений (которое в точке оптимума выполняется, как точное равенство) целевая функция принимает одно и тоже оптимальное значение на некотором множестве точек границы области допустимых решений. Эти решения называются альтернативными оптимальными решениями. Наличие альтернативных решений можно определить по оптимальной симплекс-таблице. Если в z-строке оптимальной таблицы есть нулевые коэффициенты небазисных переменных, то есть альтернативные решения.
2) Если в разрешающем столбце симплекс-таблицы все коэффициенты меньше или равны нуль, то нельзя выбрать разрешающую строку, в этом случае решение неограничено.
3) Если ограничения задачи линейного программирования несовместны (т.е. они не могут выполняться одновременно), то задача не имеет допустимых решений. Такая ситуация не может возникнуть, если все неравенства, составляющие систему ограничений, имеют тип " ≤ " с неотрицательными правыми частями, т.к. в этом случае дополнительные переменные могут составить допустимое решение. Для других типов ограничений использются искусственные переменные. Если задача имеет решение, то в оптимальной таблице в базисе нет искусственных переменных (Ri). Если они там есть, то задача не имеет решений.
