Определение толщины зуба по делительной окружности и окружности произвольного радиуса

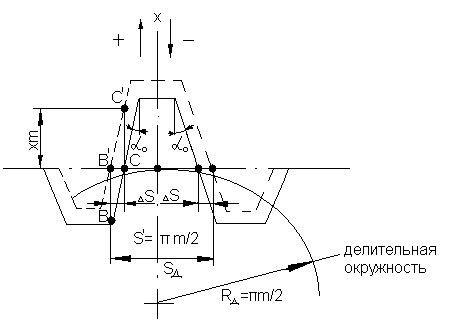
Рис. 5.10. К определению толщины зуба колеса по делительной окружности.

Толщина зуба 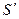(рис. 5.10) у нулевого колеса т.е. при 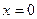, измеренная по начальной окружности равна

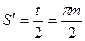(5.28)

и соответствует ширине впадины на рейке, измеренной по прямой, перекатывающейся по начальной окружности обработки (делительной окружности), которая в этом случае совпадает с начальной окружностью колеса. Дадим рейке смещение вдоль оси 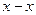, равное 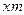. Это положение показано на рис. 9.11 штриховой линией. Тогда толщина зуба колеса (или ширины впадины на производящей рейке), измеренная по делительной окружности, будет равна

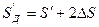(5.29)

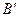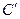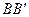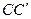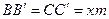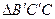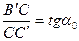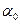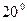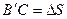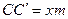При сдвиге рейки т. B переместится в положение , а т. С – в положение . Очевидно, что отрезки и равны, т.е. . Из прямоугольного имеем , где - выбранный угол зацепления при нарезании колеса (обычно ). Или т.к. и , то

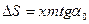(5.30)

Величина сдвига x, являясь величиной алгебраической, может иметь знак плюс или минус. Подставляя полученное выражение в равенство (9.29) и учитывая выражение (9.28), получаем

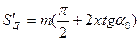(5.31)

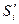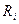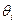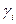Толщина зуба , измеренная по любой окружности радиуса (рис. 5.11 и 5.12), определяется из следующих условий. Сумма углов и равна 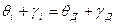, откуда пр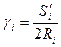и

и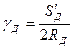

получаем

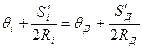
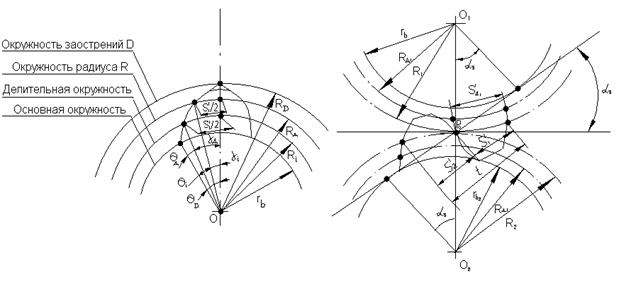
Рис. 5.11. К определению толщины зуба колеса по окружности произвольно заданного радиуса.

Рис.5.12. К выводу формулы для определения монтажного угла зацепления

Далее, используя функцию, описывающую эвольвенту боковой поверхности зуба:

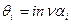и ,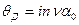

то

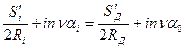, (5.32)

откуда

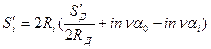(5.33)

Подставляя в формулу (5.33) вместо 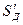выражение (5.31) получаем окончательно

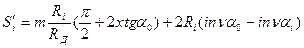(5.34)

где угол 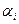определяется из условия 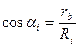(рис. 5.11)

С помощью формулы (5.34) может быть определена толщина зуба на окружности любого заданного радиуса .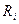

Формулы (5.33) и (5.34) позволяют проверить, не имеет ли зуб заострения, т.е. не пересекаются ли боковые профили зуба в т. D (рис.5.11). На окружности заострения (рис. 5.11) толщина зуба равна нулю. Следовательно, в равенстве (5.33) следует положить 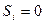, , 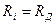где 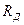- радиус окружности заострения и 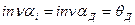откуда

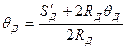
т.к. 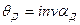, то определив угол 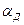, можно найти величину радиуса 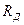окружности заострения из условия .

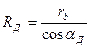Обычно толщина зуба по окружности выступов не должна быть меньше (0,25…0,3)m.

5.12. Определение угла зацепления 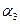для колёс, нарезанных со сдвигом рейки

Угол зацепления 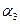, совпадает с углом зацепления 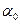только для нулевых колес. Величину этого угла определяем из следующих условий.

По формуле (5.33) размеры толщины 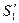и 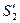зубьев колёс 1 и 2 (рис.9.12), измеренные по начальным окружностям, равны

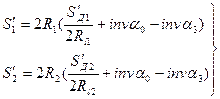(5.35)

где 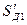и 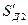- толщины зубьев 1 и 2, измеренные по их делительным окружностям радиусов 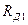и .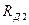

Т.к. при беззазорном зацеплении толщина зуба по начальной окружности одного колеса равна ширине впадины другого колеса и

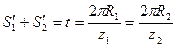, (5.36)

то, подставляя в равенство (5.36) вместо 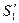и 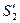их значения получаем

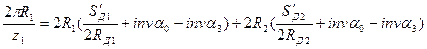(5.37)

Принимая во внимание, что 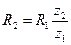и 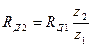, после преобразований, выразив уравнение (5.37) через 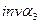, получаем

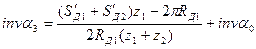(5.38)

подставляя в формулу (5.38) величины 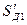и 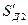, определяемые по формуле (5.31),

,

,

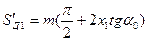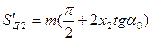и величину 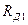, равную ,

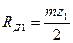окончательно имеем:

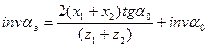
(5.39)

Анализ зависимости (5.39) показывает, что с увеличением суммарного сдвига 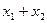увеличивается и монтажный угол зацепления. Из формулы (5.39) также следует, что для нулевой передачи, когда-либо 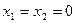, или 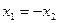, всегда имеем

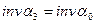, т.е. .

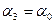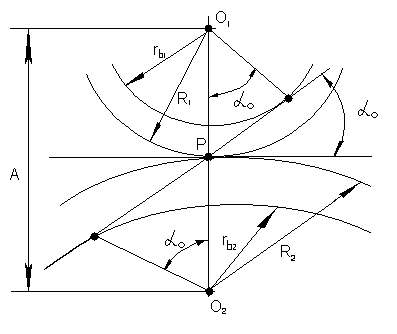
Рис. 5.13. к определению расстояние между центрами колёс.

5.13. Определение геометрических размеров колёс со сдвигом

Расстояние A (рис.5.13) между осями колёс, нарезанных со сдвигом, будет равно

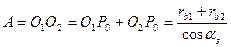
Т.к. для колёс с углом зацепления 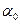расстояние 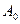между осями равно 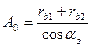, то, следовательно 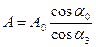, откуда, так как 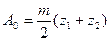окончательно получаем

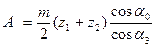(5.40)

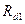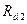Радиусы и окружностей головок колёс 1 и 2 выражаются по формулам

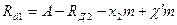(5.41)

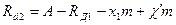(5.42)

Формулы для радиусов 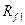и 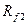окружностей впадин имеют вид

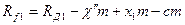(5.43)

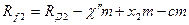(5.44)

где с=0,25- коэффициент радиального зазора.

Коэффициент перекрытия может быть определён по формуле 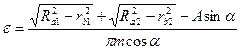, при этом величина шага t по начальной окружности при условии нарезания колеса со сдвигом должна быть принята равной

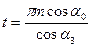
Соответственно угол 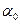в формуле (для 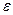) должен быть принят равным .

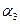Таким образом, формула для определения коэффициента перекрытия 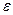для колёс, нарезанных со сдвигом, будет иметь следующий вид:

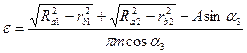(5.45)