Само множество может быть элементом другого множества.
Подмножество
Определение 8.
Пусть A и B – какие-то два множества. Если любой элемент x множества A является элементом множества B, то говорят, что множество A является подмножеством множества B и обозначают этот факт как 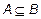 или
или  .
.
Это же определение можно переписать на языке сокращений:
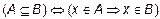 .
.
Читается оно так: "Если элемент x принадлежит множеству A, то x принадлежит множеству B". Из введенного определения, очевидно, следует утверждение, если 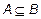 и
и  , то A=B, т.е. множества A и B состоят из одних и тех же элементов.
, то A=B, т.е. множества A и B состоят из одних и тех же элементов.
Замечание!!!
Пустое множество 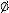 по определению считается подмножеством любого множества, т. е.
по определению считается подмножеством любого множества, т. е. 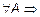
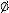
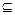 A.
A.
Определение 9.
Подмножество A множества B, отличное от самого множества B и 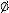 , называется собственным подмножеством и обозначается
, называется собственным подмножеством и обозначается 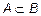 .
.
Это так называемое "строгое" включение множества A в множество B.
ПРИМЕР 6.
 ,
, 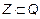 . Однако интервалы [1,2] и (1,3] не удовлетворяют никаким условиям включения. В каждом из этих множеств есть элементы, не принадлежащие другому множеству.
. Однако интервалы [1,2] и (1,3] не удовлетворяют никаким условиям включения. В каждом из этих множеств есть элементы, не принадлежащие другому множеству.
Свойства включений
1)  ;
;
2) 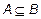 и
и 
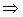 A=B;
A=B;
3) 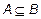 и
и 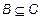
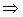
 .
.
Определение 10.
Подмножества B и 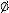 множества B называются его несобственными подмножествами.
множества B называются его несобственными подмножествами.
Вывод!!!
| |
ПРИМЕР 7.
Всевозможные подмножества множества A={a,b} суть 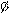 , {a}, {b}, {a,b}, из которых {a}, {b} – собственные подмножества множества A.
, {a}, {b}, {a,b}, из которых {a}, {b} – собственные подмножества множества A.
Заключение
В лекции начато изучение высшей математики. Введено важное понятие множества. Важно понять, что множество – это совокупность элементов. Одно множество может быть элементом другого множества, поэтому, рассматривая какие-либо математические операции, действия, графики и т. д., важно определиться, каким множеством мы оперируем, иначе все выводы нельзя принять верными.
Отметим следующее:
- множество есть многое, мыслимое нами как целое;
- само множество может быть элементом другого множества;
- для быстроты и простоты записи используют сокращения;
- пустое множество единственное;
- в равных множествах последовательность элементов не важна;
- важно различать 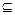 – подмножество и
– подмножество и  – собственное подмножество.
– собственное подмножество.
Литература
1. Москинова Г.И. Дискретная математика. – М.: Логос, 2002. – 240 с.
2. Яблонский Я. В. Введение в дискретную математику. – М.: Высшая школа, 2001, - 384 с.
3. Шипачев В.С. Основы высшей математики. - М.: Высшая школа,1998.
4. Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики. – М.: Наука, 1989, - 659 с.
| |
Алгебра множеств
Операции над множествами. Диаграммы Венна
Принцип двойственности
