Момент инерции Ii материальной точки относительно некоторой оси вращения определяется как произведение ее массы mi; на квадрат расстояния ri , до оси вращения

		Ii = mi ri2.

I =

Момент инерции твердого тела равен сумме моментов инерции отдельных его частей - материальных точек

.

Если абсолютно твердое тело имеет форму тела вращения относительно оси, проходящей через его центр инерции, то выражение для момента инерции принимает более простой вид:

I = kmR², (1)

где m и R - масса и радиус тела соответственно;

k – коэффициент, зависящий от формы тела.

Для обруча и тонкостенного цилиндра k = 1, для сплошного цилиндра и диска k =1/2, для шара k = 2/5.

Если ось вращения не проходит через центр инерции тела, то для вычисления его момента инерции пользуются теоремой Штейнера:

Момент инерции I относительно произвольной оси равен сумме момента инерции I_о относительно оси, проходящей через центр масс тела параллельно данной, и произведения массы тела на квадрат расстояния а между осями

I = Iо + mа2

(2)

Момент инерции системы тел относительно некоторой оси равен сумме моментов инерции относительно этой оси всех тел, входящих в систему:

I = I₁ + I₂ + I₃ + ... + I_N. (3)

Момент инерции тела как характеристика его инертных свойств входит в уравнения динамики вращательного движения. При вращении твердого тела относительно неподвижной оси основное уравнение динамики вращательного движения можно записать в виде:

M =Ie , (4)

где М– проекция результирующего момента всех внешних сил на ось вращения; e – угловое ускорение.

Так как угловое ускорение может быть записано как вторая производная по времени от угла поворота:

то уравнение (4) можно представить в виде

.

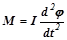Метод измерения и описание аппаратуры

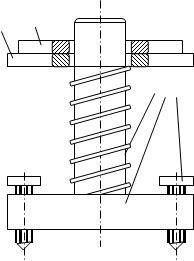
Для измерения момента инерции в данной лабораторной работе используются крутильные колебания изображенного на рисунке устройства, состоящего из диска 1 и лежащих на нем одного или нескольких тел 2. В работе используется эталонное тело (ЭТ) с известным моментом инерции. Диск расположен на станине 3, имеющей винты 4 для корректировки горизонтального положения плоскости диска. Пружина 5 служит для возвращения диска в положение равновесия и создания колебательного движения относительно вертикальной оси (рис. 61.1).

При отклонении диска на некоторый угол j (в пределах упругой деформации пружины) со стороны пружины на диск действует возвращающая сила, проекция момента которой пропорциональна углу отклонения:

М = - bj, (6)

где b — упругая постоянная пружины.

Если пренебречь влиянием силы трения, то уравнение движения диска на основании формул (5) и (6) примет вид

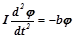_, (7)

1 2

5 3 4

Рис.61.1.

где I – момент инерции диска с лежащими на нем грузами.

Решение этого уравнения имеет вид

	j = j0 cos (wt + a),

то есть угол отклонения диска от положения равновесия изменяется по гармоническому закону и вся система совершает гармонические колебания с амплитудой j₀ и круговой частотой w. Величину (wt + a) называют фазой колебания, a – начальной фазой, определяющей угол отклонения j при t = 0.

Найдя первую и вторую производные угла j по времени t и подставив их в уравнение (7), получим

-I w² j₀ cos (wt + a) = - b j₀ cos (wt +a) ,

откуда найдем

,

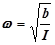а затем формулу для периода колебаний T:

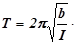
Если колеблется только диск, то его период колебаний

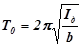, (8)

где I_д – момент инерции диска без грузов.

Если на диске лежит эталонное тело, то период колебаний системы T_ЭТ, в этом случае можно записать аналогично:

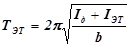. (9)

Используя выражения (8) и (9), получим:

.

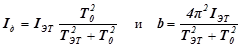Если диск колеблется вместе с телом, момент инерции которого I_x требуется определить, то период его колебаний

,

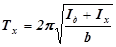откуда

I_x = .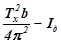

Используя полученные выражения для b и I_д, получим окончательную формулу для определения момента инерции исследуемого тела:

	.

Порядок выполнения работы

1. Отклонив диск без грузов на некоторый угол (j » 90°) определите время t нескольких полных колебаний (n = 5 ¸ 6). Рассчитайте период колебаний диска Т₀. Повторите измерения.

2. Поместите на середину диска эталонное тело, измерьте время нескольких полных колебаний. Рассчитайте период колебаний системы с эталонным телом Т_ЭТ. Повторите измерения.

Полученные данные занесите в табл. 1 и вычислите средние значения Т₀ и T_ЭТ.

Таблица 1

№ опыта	Число колебаний, n	Колебания диска без грузов	Колебания диска с эталонным телом
t, c	T0, c	t, c	TЭТ, c
Средняя величина

3. Вместо эталонного тела поместите на середину диска одно из исследуемых тел, приведите систему в колебательное движение, измерьте время нескольких колебаний и определите период колебаний Т_х. Вычислите момент инерции исследуемого тела I_x. Повторите измерения; результаты занесите в табл. 2.

Таблица 2

Номер тела	Число колебаний n	t, c	Tх, c	Ix, кг×м2

4. Рассчитайте средние значения моментов инерции обоих тел. Запишите результаты в табл. 3.

5. Вычислите моменты инерции обоих тел по их массам и радиусам, используя формулу (1) и учитывая форму тел. Запишите результаты в табл. 3.

Таблица 3

Номер тела	Форма тела	Масса тела m, кг	Радиус тела R, м	Ix , кг×м2 по формуле (1)	Ix ср, кг×м2 из табл.2

6. Поместите на середину диска оба тела, положив их одно на другое. Приведите систему в колебательное движение и определите время t нескольких колебаний. Определите период колебаний и момент инерции системы из двух тел. Вычислите момент инерции системы из двух тел как сумму моментов инерции отдельных тел I_{x ср}, взятых из табл. 3. Результаты запишите в табл. 4.

Таблица 4

№ опыта	n	t, c	T, c	Момент инерции двух тел по формуле (10) Ix кг×м2
Среднее значение
Момент инерции двух тел: Ix = Ix1 ср + Ix2 ср

7. Поместите одно из исследуемых тел на некотором расстоянии от центра диска. Приведите систему в колебательное движение, измерьте время нескольких колебаний. Вычислите момент инерции тела по формуле (10). Измерения повторите. Найдите среднее значение момента инерции. Измерьте расстояние а от центра инерции тела до оси вращения. Рассчитайте момент инерции тела по теореме Штейнера, воспользовавшись значением момента инерции тела I_{x ср} из табл. 3. Результаты занесите в табл. 5.

Таблица 5

№ опыта	n	t, c	T, c	Момент инерции по формуле (10), Ix кг×м2
Среднее значение
Момент инерции по формуле (2): I = …..

8. Определите случайные ошибки измерений T₀, T_ЭТ, Т_Х1, Т_Х2:

DT₀ ; DT_ЭТ,DТ_Х1,DТ_Х2.

В частности, DТ₀ = a_ст×S.

Здесь a_ст – коэффициент Стьюдента;

S – поправка Стьюдента, определяемая по формуле:

,

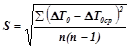где n – число измерений.

Значение коэффициента Стьюдента для указанной преподавателем доверительной вероятности следует найти по табл. 1 из [3]. Аналогичным образом рассчитываются DT_ЭТ,DТ_Х1,DТ_Х2.

9. Вычислите относительную погрешность dI измерения момента инерции тела № 1 и тела № 2 по формуле:

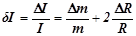, (11)

где Dm - погрешность измерения массы тела;

DR – погрешность измерения радиуса тела, которая определяется масштабом линейки, используемой для измерения радиуса тела.

Контрольные вопросы

1. Что называют моментом инерции точки и твердого тела?

2. Чему равны моменты инерции цилиндра, диска и шара относительно их осей симметрии?

3. Сформулируйте основной закон динамики вращательного движения твердого тела.

4. Сформулируйте теорему Штейнера.

5. Получите формулу для расчета момента инерции тела по периоду колебаний диска.

РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА

1. Савельев И. В. Курс общей физики: В 3-х т. – М.: Наука, 1987. – Т. 1, 432 с.

2. Методические указания к лабораторным работам по физике. Механика. Работы 60 - 63. - М.: Изд. МИИТа, 1976. - Раздел «Ошибки измерения физических величин. Вычисление ошибок косвенных измерений».

3. Расчет погрешностей в лабораторных работах физического практикума. Методические указания к вводным занятиям в физическом практикуме/ Н.А.Гринчар, Ф.П.Денисов, Б.А.Курбатов и др.; Под общ. ред. Ф.П.Денисова. - М.: МИИТ, 1995. - 38 с.

РАБОТА № 63
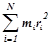
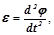
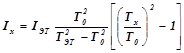