Уравнение динамики вращательного движения

Твердого тела вокруг неподвижной оси.

Момент импульса твердого тела при вращательном движении вокруг оси z вычисляется как

.

Тогда уравнение динамики вращательного движения примет вид:

.

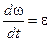Если тело твердое, то , поэтому, с учетом того, что (угловое ускорение), получаем выражение

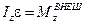
Это уравнение динамики вращательного движения твердого тела вокруг неподвижной оси:

угловое ускорение вращательного движения твердого тела вокруг неподвижной оси прямо пропорционально величине момента внешних сил относительно этой оси.

Замечание. По аналогии со вторым законом Ньютона, в котором ускорение определяется силой, уравнение динамики вращательного движения твёрдого тела дает связь между угловым ускорением и моментом силы. В этом смысле момент инерции тела играет роль меры инертности при вращательном движении.

Примеры вычисления моментов инерции.

1) Момент инерции тонкого кольца (прямого тонкостенного цилиндра) массы m и радиуса R относительно оси z, перпендикулярной плоскости кольца, проходящей через центр кольца

.

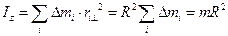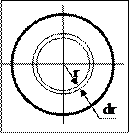2) Момент инерции диска (сплошного цилиндра) массы m и радиуса R относительно оси z, перпендикулярной к плоскости диска, проходящей через центр диска (сплошного цилиндра).

Выделим тонкий цилиндр радиусом r и толщиной dr.

Масса этого цилиндра , .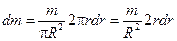

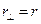Поэтому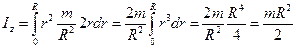

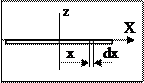3) Момент инерции тонкого стержня относительно оси z, являющейся срединным перпендикуляром. Масса стержня m, длина L.

Выделим на расстоянии x от оси маленькую часть стержня длиной dx.

Масса этой част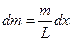и и 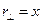. Поэтому

.

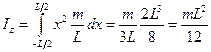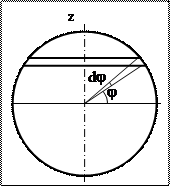4) Момент инерции тонкостенного шара относительно любой оси симметрии z. Масса шара m, радиус R.

Выделим на поверхности сферы кольцевой сегмент, для которого ось z является осью симметрии. Сегмент опирается на малый центральный угол dj, положение сегмента определяется углом j, отсчитываемым от плоскости экватора, перпендикулярной оси z.

Тогда радиус кольца ,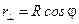

его масса 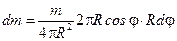, поэтому

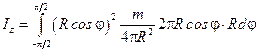или

.

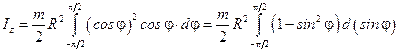
5) Момент инерции сплошного шара относительно любой оси симметрии z. Масса шара m, радиус шара R.

Представим шар как набор вложенных друг в друга тонкостенных сфер переменного радиуса r и толщиной dr. Масса одной такой сферы .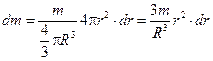

Момент инерции такой сферы .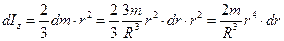

Поэтому

.

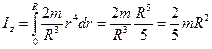Теорема Гюйгенса-Штейнера

Как связаны между моменты инерции твердого тела относительно двух параллельных осей?

Рассмотрим две параллельные оси z₁ и z₂. Введем две системы координат так, чтобы их оси х и у были параллельны друг другу, причем вторая система координат была получена параллельным переносом из первой на вектор, перпендикулярный осям z₁ и z₂ . Тогда расстояние между осями будет равно .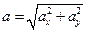

В этом случае координаты любой i-й малой частицы тела связаны соотношениями

, , .

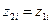Квадрат расстояния от этой точки до первой оси z₁: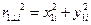

и до второй оси z₂ .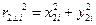

Вычисляем момент инерции относительно второй оси:

,

.

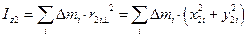В этом равенстве

- момент инерции тела относительно оси z₁,

,

.

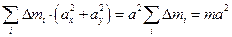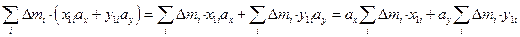Учтём, что 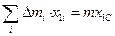и (где x_1С и y_1С – координаты центра масс тела в 1й системе координат) и получим

Если предположить, что ось z₁ проходит через центр масс тела, то x_1С =0 и y_1С =0, поэтому в этом случае выражение упрощается:

.

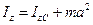Это выражение носит название теоремы Гюйгенса-Штейнера: момент инерции твердого тела относительно произвольной оси равен сумме момента инерции тела относительно параллельной оси, проходящей через центр масс тела и квадрата расстояния между осями, умноженного на массу тела.

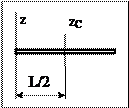Пример. Момент инерции стрежня относительно оси, проходящей через край стержня, перпендикулярно ему, равен сумме момента инерции относительно срединной оси и массе, умноженный на квадрат половины длины стержня:

.

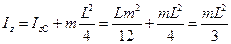Пример. Рассмотрим движение грузов на невесомой нерастяжимой нити, перекинутой через блок (диск). Массы грузов m₁ и m₂ (m₁ < m₂), масса блока m. Трения в оси блока нет. Нить не скользит по блоку. Силами сопротивления в воздухе пренебрегаем. Найти ускорение грузов. Радиус блока R.

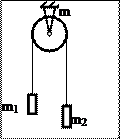Решение. Фиксируем систему отсчета, в которой ось блока неподвижная. Предполагаем, что эта система отсчета инерциальная. Ось z системы координат в этой системе отсчёта направим вдоль оси вращения блока («от нас»).

«Мысленно» разбиваем систему на части и находим силы между частями системы в соответствие со вторым и третьим законами Ньютона.

При этом учтём, что нить невесомая (масса любой части нити равна нулю), поэтому, если кусок нити движется под действием (растягивающих) сил, то из второго закона Ньютона

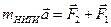
следует при m_НИТИ=0, что эти силы равны по величине F₂=F₁.

Нить также является нерастяжимой, поэтому ускорения всех точек нити одинаковые по величине. Следовательно, ускорения грузов одинаковые по величине.

Нить не скользит по блоку – это значит, что скорости точек обода диска равны скоростям (соответствующих) точек нити. Следовательно, их тангенциальные ускорения тоже одинаковые.

Из всего этого следуют уравнения:

- равенства соответствующих сил натяжения

, ,

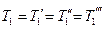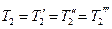- равенства ускорений

,

- равновесия оси блока

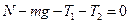
- динамики центров масс грузов

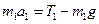
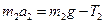
- динамики вращательного движения блока вокруг оси z

.

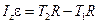Обозначим величину ускорения грузов как а.

В данном случае момент инерции блока (диска) относительно оси вращения 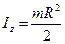, поэтому из уравнения динамики вращательного движения

находим 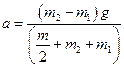.