Цилиндрические поверхности

Определение. Линейчатой называется поверхность, через каждую точку которой проходит хотя бы одна прямая, принадлежащая поверхности.

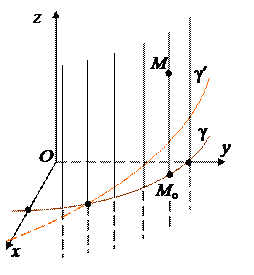
Определение. Цилиндрической называется поверхность, которую образует множество параллельных прямых (образующих), проходящих через каждую точку некоторой кривой (направляющей).

Пусть F – цилиндрическая поверхность. Выберем декартову СК так, чтобы ось Oz была параллельна

образующим. Если, при этом, направляющая g¢ не лежит в плоскости Oxy, то мы ее спроецируем в эту плоскость, и получим некоторую кривую g. Если теперь мы возьмем g в качестве направляющей, то получим ту же поверхность F. Поэтому будем с самого начала считать, что направляющей служит кривая g, лежащая в плоскости Oxy. Пусть

j(x, y) = 0 – (1)

ее уравнение в плоскости Oxy (в пространстве она задается системой из двух уравнений: j(x, y) = 0 и z = 0). Пусть M(x, y, z) – произвольная точка поверхности F. Тогда ее проекция на плоскость Oxy будет точка M_o(x, y, 0); и эта точка должна принадлежать кривой g. Поэтому ее координаты удовлетворяют (1). Но тогда этому уравнению будут удовлетворять и координаты точки M_o: ведь координаты x и y у этих точек одинаковы, а z в уравнение не входит.

Обратно, пусть координаты точки M(x, y, z) удовлетворяют (1). Тогда этому же уравнению удовлетворяют и координаты точки M_o(x, y, 0), а т.к. M_oÎOxy, то M_oÎg. При этом, M и M_o лежат на одной прямой, параллельной оси Oz Þ MÎF.

Итак, мы установили, что (1) и есть уравнение поверхности F, т.е. уравнение цилиндрической поверхности совпадает с уравнением ее направляющей кривой g в плоскости Oxy, если образующие параллельны оси Oz. Аналогично, если образующие параллельны Oy, то уравнение цилиндрической поверхности совпадает с уравнением направляющей кривой в плоскости Oxz.

И обратно, если в уравнении поверхности отсутствует, например, координата x, то сразу можем сделать вывод, что эта поверхность цилиндрическая, а ее образующие параллельны Ox.

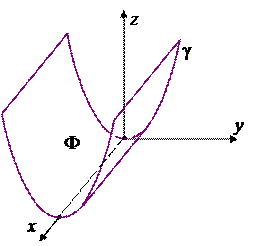Пример. Пусть поверхность задана уравнением y² = 2z . Тогда это цилиндрическая поверхность, ее образующие параллельны Ox, а направляющей служит парабола

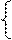y² = 2z ,

x = 0 .

Такая поверхность называется «параболический цилиндр».

Поскольку уравнение цилиндрической поверхности совпадает

с уравнением направляющей кривой, то список цилиндрических поверхностей второго порядка совпадает со списком их направляющих кривых второго порядка.

1. Эллиптический цилиндр	+ = 1
2. Мнимый эллиптический цилиндр ( Æ )	+ = –1
3. Гиперболический цилиндр	– = 1
4. Параболический цилиндр	y2 = 2pх
5. Пара пересекающихся плоскостей	a2x2 – b2 y2 = 0
6. Пара мнимых плоскостей, которые пересекаются по действительной прямой	a2x2 + b2 y2 = 0
7. Пара параллельных плоскостей	x2 = a2
8. Пара совпадающих плоскостей	x2 = 0
9. Пара мнимых параллельных плоскостей ( Æ )	x2 = – a2

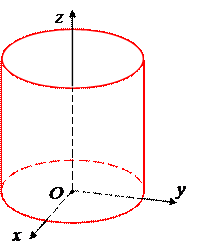
Упражнение. Самостоятельно определите, какая поверхность изображена на каждом из следующих рисунков.

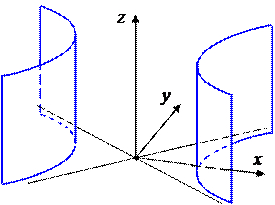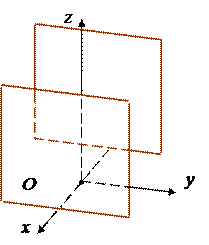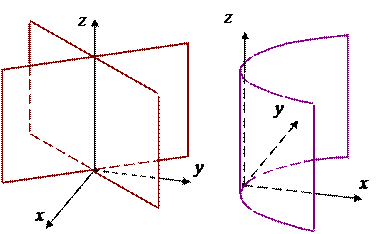Конические поверхности.

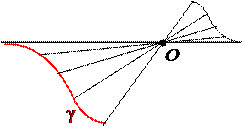
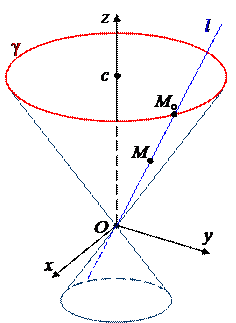Определение. Конической называется поверхность, которую образует множество всех прямых (образующих), проходящих через каждую точку некоторой кривой (направляющей), и через некоторую точку O (вершину).

Выберем декартову СК так, чтобы начало координат совпадало с вершиной конической поверхности F. Пусть F(x, y, z) = 0 – уравнение поверхности F в этой СК. Поскольку мы рассматриваем только поверхности второго порядка, то F – многочлен второй степени от 3 переменных. Тогда функция двух переменных

j(x, y) = F(x, y, c)

будет также многочленом второй степени для любого cÎR, а система

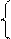j(x, y) = 0,

z = c

будет задавать сечение поверхности F плоскостью z = c. Получающуюся в сечении кривую g выберем в качестве

направляющей. Т.к. j(x, y) – многочлен 2 степени, то g – кривая 2 порядка. Если g – центральная, то можем считать, что ось Oz проходит через ее центр.

Предположим сначала, что направляющая – эллипс

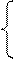g: + – 1 = 0, (*)

z = c

Пусть M(x₁, y₁, z₁) – произвольная точка поверхности F. Тогда вся прямая OM должна лежать на поверхности. Ее параметрическое уравнение:

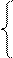x = x₁t,

OM: y = y₁t,

z = z₁t.

Пусть она пересекает направляющую g в точке M_o(x_o, y_o, c). Тогда ее координаты должны удовлетворять уравнению прямой OM:

x_o = x₁t, x_o = x₁c/z₁,

y_o = y₁t, Þ y_o = y₁c/z₁,

c = z₁. t = c/z₁.

А теперь подставим найденные выражения в уравнение эллипса:

+ – 1 = 0.

Домножим это уравнение на z₁/c, и получим

+ – = 0. (2)

Обратно, пусть координаты точки M(x₁, y₁, z₁) удовлетворяют уравнению (2). Тогда этому уравнению удовлетворяют и координаты любой точки на прямой OM:

+ – = t ²( + –) = t ²·0 = 0,

а подставив в (2) z = c, получим уравнение эллипса (*). Значит, (2) и есть уравнение конической поверхности. Опуская индексы, окончательно получаем каноническое уравнение конуса.

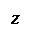+ – = 0.

Аналогично, если направляющая кривая – это гипербола

– –1 = 0,

z = c ,

получим уравнение конической поверхности

– – = 0 Û – + + = 0.

Это такой же «эллиптический» конус, только ось его будет не Oz, а Oz¢.

Пусть теперь направляющая g – это парабола

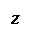
x² = 2py,

z = c .

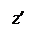
Тогда тем же способом получим уравнение

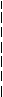
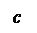
x² = yz. (**)

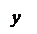
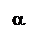
Повернем СК на 45^о вокруг оси Ox. Тогда формулы замены координат имеют вид

x = x¢,

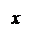y = (y¢+ z¢),

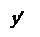z = (– y¢+ z¢).

Подставим эти формулы в (**), и обозначив a² = p/c, получим

x² = a²(– y¢ ² + z¢ ²) Û + y¢ ² – z¢ ² = 0.

Таким образом, уравнение (**) тоже определяет конус, ось которого является биссектрисой угла yOz. При этом, оси Oy и Oz принадлежат конусу. Поэтому плоскость, в которой лежит направляющая g, параллельна образующей.

Мы уже говорили в предыдущей главе, что эллипс, гипербола и парабола – это конические сечения. Теперь мы в этом убедились.

Если направляющей служит пара прямых, то коническая поверхность представляет собой пару плоскостей, обязательно пересекающихся или совпадающих, т.к. обе плоскости должны проходить через начало координат. Эти поверхности относятся также к цилиндрическим и они были рассмотрены в предыдущем параграфе.

Итак, мы установили, что существуют 4 типа конических поверхностей:

1. Конус + – = 0.

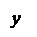
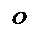
2. Пара пересекающихся плоскостей a²x² – b² y² = 0 .

3. Пара мнимых пересекающихся плоскостей a²x² + b² y² = 0 .

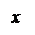4. Пара совпадающих плоскостей x² = 0.

Поверхность вращения.

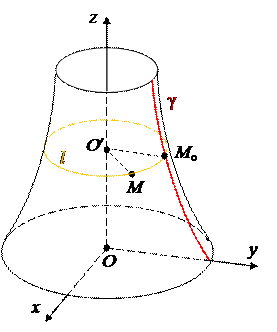Пусть некоторая кривая g расположена в плоскости Oyz. Будем вращать ее вокруг оси Oz. Получим некоторую поверхность F, которая называется поверхностью вращения. Каждая точка кривой g описывает окружность – параллель, центр которой лежит на оси Oz.

Пусть

j(y, z) = 0 – (3)

уравнение кривой g в плоскости Oyz. Тогда в пространстве она задается системой

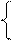j(y, z) = 0,

x = 0.

Пусть M(x, y, z) – произвольная точка поверхности F. Тогда она лежит на одной из таких параллелей l и может быть получена поворотом точки M_o(0, y_o, z_o) = g I l. Очевидно, что z_o= z (*), и центр O¢ параллели l имеет координаты O¢(0, 0, z). Кроме того, ½O¢M½ =½O¢M_o½ . В координатах это условие имеет вид

y_o= . (**)

Координаты точки M_o должны удовлетворять уравнению (3): j(y_o, z_o) = 0. Подставляя сюда (*) и (**) получаем

j(, z) = 0. (4)

Обратно, пусть координаты точки M(x, y, z) удовлетворяют (4). Тогда, если выполнено (*) и (**), то этому уравнению будут удовлетворять координаты точки M_o(0, y_o, z_o), а значит M_oÎg. Кроме того, в силу (*) и (**) точка M_o лежит на одной параллели с M, а значит M может быть получена поворотом точки M_o вокруг оси Oz Þ MÎF.

Итак, мы доказали, что (4) есть уравнение поверхности вращения F. Таким образом, для того чтобы из уравнения кривой g получить уравнение поверхности вращения F, мы в уравнении кривой оставляем без изменения координату z, а y заменяем: y a .

Обратно, если в уравнении поверхности можно выделить , и при этом, нигде более координаты x и y в уравнение не входят, то мы сразу можем сделать вывод, что наша поверхность есть поверхность вращения вокруг Oz.

Пример 1. Пусть g – окружность в плоскости Oyz радиуса b с центром в точке A(0, a, 0)ÎOy, a > b. Будем вращать ее вокруг Oz. Получим поверхность, которая называется тором. Уравнение окружности в плоскости Oyz имеет вид:

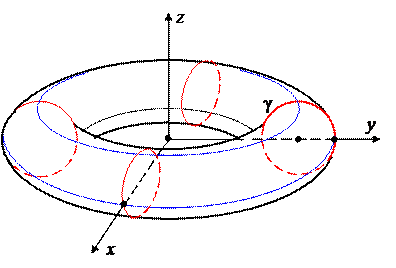(y – a)² + z ² = b².

Вращаем вокруг Oz. Поэтому z оставляем без изменений, а y заменяем:

y a :

( – a)² + z² = b².

Получили уравнение тора. Заметим, что тор не относится к поверхностям 2 порядка.

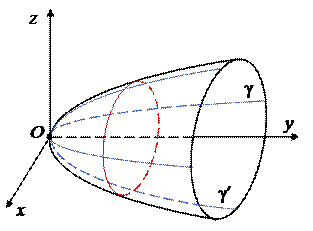Пример 2. Поверхность F задается уравнением

x² + z² = 2y.

Мы можем переписать его так:

()² = 2y.

Координаты x и z входят в уравнение только в выражении . Значит, наша поверхность – это поверхность вращения вокруг Oy. Для того, чтобы

получить уравнение кривой, которая вращается, мы заменяем на x и получаем уравнение кривой g в плоскости Oxy: x² = 2y. В пространстве эта кривая задается системой

x² = 2y,

z = 0.

Точно так же мы можем заменить на z и получить уравнение кривой g¢ в плоскости Oyz: z ² = 2y. Вращая вокруг Oy первую или вторую кривую, мы получим одну и ту же поверхность.

Эллипсоид.

Определение. Эллипсоидом называется поверхность F, имеющая каноническое уравнение вида

+ + = 1. (5)

Исследуем ее форму методом параллельных сечений. В сечениях плоскостями z = h получаем кривую

+ = 1– (*)

Если ½ h ½ ¹ c , то обозначим a¢² = a²½1– ½ , b¢² = b²½1– ½ .

При ½ h ½< c получаем эллипсы + = 1, полуоси которых a¢ и b¢ достигают максимального значения a и b при h = 0.

При ½ h ½ > c получаем мнимые эллипсы + = –1 (Æ). А при h = ± c из (*) получаем уравнение + = 0, которое задает только одну из точек C₁(0, 0, c) или C₂(0, 0,– c).

Аналогично, в сечениях плоскостями x = h , или y = h в случае ½ h ½< a , или ½ h ½< b, получаем только эллипсы, полуоси которых достигают максимальных значений при h = 0. При h = ± a , или h = ± b будем получать одну точку.

Прочие геометрические свойства эллипсоида.

1.Из уравнения (5) получаем, что ½ x ½£ a, ½ y ½£ b, ½ z ½£ c (если ½ x ½> a, то уже первое слагаемое в (5) будет больше 1, а к нему еще надо что-то прибавить). Значит, весь эллипсоид содержится в пар-де, который определяется этими неравенствами.

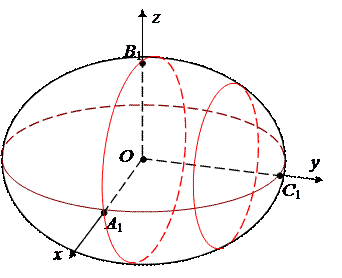2. Координатные оси пересекают эллипсоид в точках A₁(a, 0, 0), A₂(– a, 0, 0), B₁(0, b, 0), B₂(0,– b, 0), C₁(0, 0, c), C₂(0, 0,– c), которые называются вершинами эллипсоида.

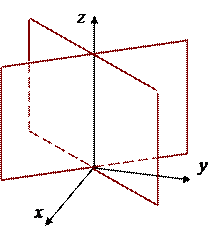
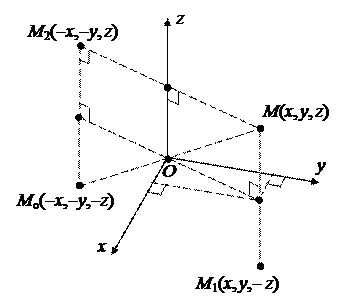3.Координатные оси являются осями симметрии эллипсоида, координатные плоскости – плоскостями симметрии, начало координат О – центром симметрии.

Действительно, пусть M(x, y, z) – произвольная точка эллипсоида. Тогда ее координаты (x, y, z) удовлетворяют уравнению (5). Но тогда этому уравнению удовлетворяют также тройки чисел ( x,– y,– z), (– x, y,– z), (– x,– y, z), (x, y,– z), (x,– y, z), (– x, y, z), (– x,– y,– z), которые определяют точки симметричные M соответственно относительно осей Ox, Oy, Oz, плоскостей Oxy, Oxz, Oyz и точки O. Поэтому все эти точки тоже принадлежат эллипсоиду.

На рисунке показано, как изменяются координаты точки при симметрии относительно оси Oz, плоскости Oxy и точки O.

4. При a = b эллипсоид будет поверхностью вращения вокруг Oz. Действительно, в этом случае его уравнение можно переписать так:

+ = 1.

Аналогично, при a = c эллипсоид будет поверхностью вращения вокруг Oy, а при b = c – вокруг Ox.

При a = b = c эллипсоид будет сферой:

x² + y² + z² = a² (**).

Произвольный эллипсоид может быть получен из сферы (**) в результате равномерного сжатия (растяжения) по двум взаимно перпендикулярным направлениям. Действительно, если в (**) сделать замену координат x = x¢, y = y¢, z = z¢, то получим уравнение (5), только со штрихами.