Напряжение при изгибе и расчет балок на прочность

При поперечном изгибе балки от произвольной внешней нагрузке 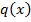в ее поперечных сечениях возникают перерезывающие силы и изгибающие моменты (рис. 8.20, а).

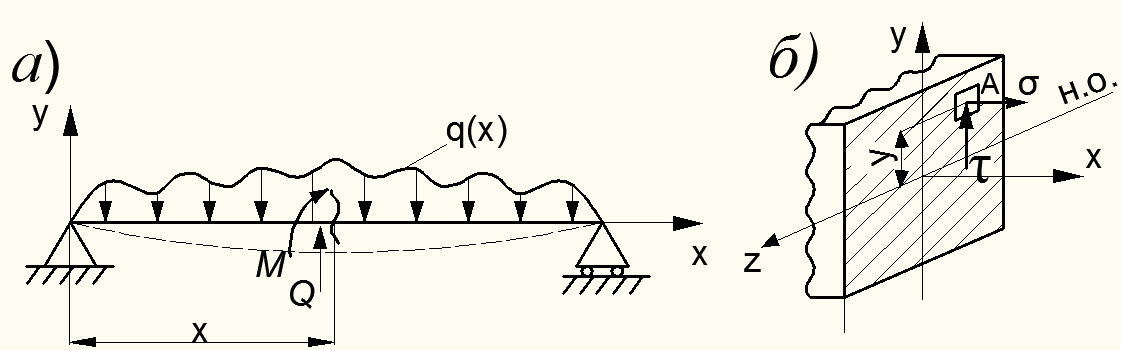
Рисунок 8.20 – Напряжения в поперечных сечениях балки при ее поперечном изгибе

К изгибающему моменту М в сечении х приводят нормальные напряжения 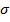, действующие перпендикулярно плоскости поперечного сечения (рис. 8.20, б). Перерезывающая сила является равнодействующей касательных напряжений 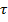, действующих в плоскости сечения.

Приведем формулы для вычисления этих напряжений, необходимых для проверки прочности балки.

Рассматривая деформацию волокна балки, проходящего через точку А сечения балки (см. рис. 8.20, б), можно получить формулу для нормальных напряжений :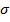

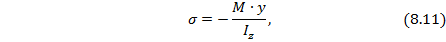
где 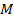– изгибающий момент в сечении х по длине балки; 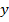– вертикальная координата т. А, отсчитываемая от нейтральной оси (н.о.) сечения, где определяется напряжение; 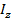– центральный осевой момент инерции сечения балки относительно центральной оси z (н.о.), проходящий через центр тяжести сечения.

Из формулы (8.11) следует, что нормальные напряжения распределяются по высоте сечения по линейному закону: для изогнутой при изгибе балки (см. рис. 8.20, а) верхние волокна балки сжимаются (такие напряжения принимаются со знаком «-»), а нижние – растягиваются (принимаются со знаком «+»). Поэтому, чтобы автоматически учесть знаки напряжений, изгибающего момента М и ординаты y, в формуле (8.11) указывается знак минус. Именно в такой форме эта формула будет применятся ниже.

График изменения нормальных напряжений по высоте изгибаемой балки (см. рис. 8.22, а) называется эпюрой (эп. 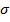), показанной на рис. 8.21, а.

Эп. показывают в плоскости сечения балки (рис. 8.21, б, в), разворачивая действительную эпюру в объемном изображении по направлению к оси z на 90˚.

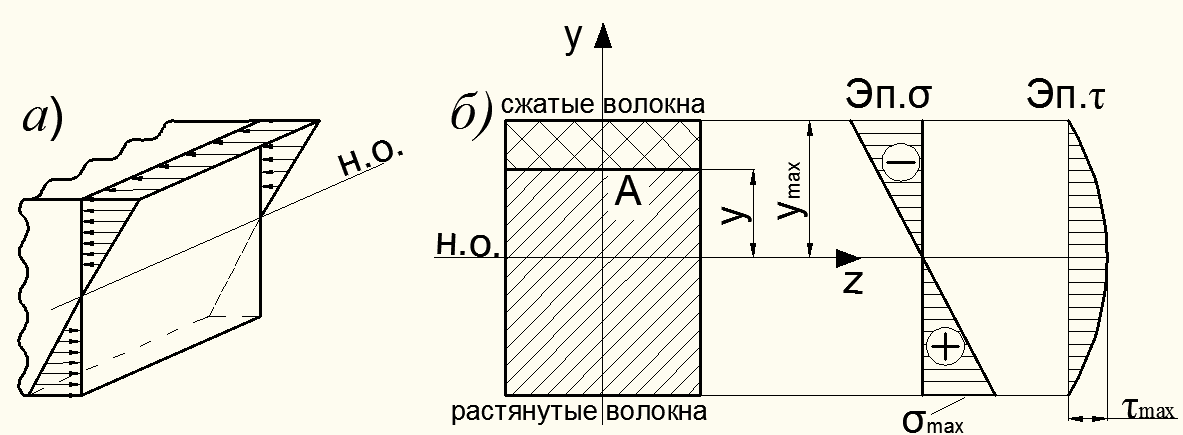
Рисунок 8.21 – Эпюры нормальных и касательных напряжений для балки прямоугольного сечения

Эпюры показываются знаками напряжений 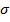, откладывая положительные значения справа, а отрицательные – слева от вертикальной линии.

Из эпюры видно, что максимальные нормальные напряжения по модулю возникают в наиболее удаленных от н.о. точках сечения балки при .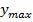

Величина 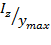в формуле (8.11), зависящая только от размеров и формы поперечного сечения балки и называемая осевым моментом сопротивления сечения, рассчитывается по формуле

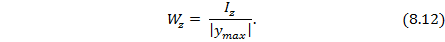
Следовательно, условие прочности на изгиб балок по нормальным напряжениям будет:

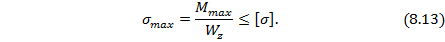
Для балок симметричного профиля относительно н.о. величина 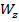одинакова для кратных точек сечения.

Для балки несимметричного поперечного сечения, например, несимметричный двутавр (рис. 8.22, а) Эп. 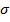показанна на рис. 8.22, б.

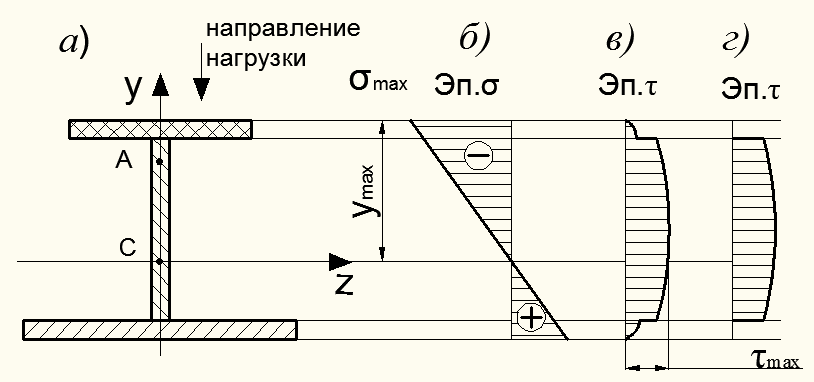
Рисунок 8.22 – Эпюры нормальных и касательных напряжений для несимметричного двутавра

Для такой балки

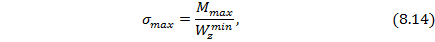
где 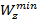– минимальный момент сопротивления сечения, .

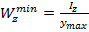Для большинства балок в различных конструкциях нормальные напряжения являются наибольшими и по ним проверяется прочность таких элементов конструкций:

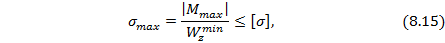
где 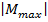– наибольший по модулю изгибающий момент в опасном сечении балки; 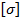– допускаемое нормальное напряжение, равное 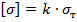( 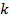– коэффициент запаса прочности, 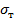– предел текучести материала).

Условие прочности (8.15) дает возможность решать такие три задачи: 1) определять напряжение, если известны изгибающий момент, действующий на балку, и момент сопротивления сечения; 2) определять допустимую нагрузку через изгибающий момент и момент сопротивления сечения; 3) определять момент сопротивления, а по нему и размеры сечения, если известны изгибающий момент и допускаемое напряжение.

Формула для касательных напряжений при поперечном изгибе балки была впервые получена Д.И. Журавским при рассмотрении условия равновесия отсеченного элемента балки и носит имя формулы Журавского:

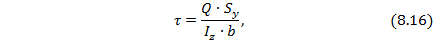
где – перерезывающая сила в сечении балки; 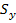– момент сопротивления части площади сечения балки по одну сторону от точки А (см. рис. 8,22, а), где рассчитывается величина 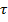; 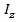– центральный момент инерции площади поперечного сечения балки, относительно горизонтальной оси z; 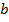– горизонтальный размер сечения балки, где вычисляется .

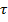Распределение касательных напряжений по высоте сечения балки называется эпюрой 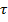(эп. 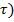и соответствует закону квадратичной параболы (см. рис. 8.22, в, г). Знаки напряжений на эп. 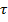не проставляются. Наибольшие касательные напряжения 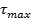возникают в точке центра тяжести сечения балки, а в крайних точках по высоте сечения – .

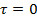Следует заметить, что для балок составного поперечного сечения (например, составной двутавр на рис. 8.22, а) в точках сопряжения стенки и полок значения будут двузначны, т.к. для стенки величина 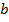формуле (8.16) соответствует толщине стенки t, а для полок величина 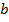равна их ширине. Поэтому на эп. 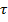(см. рис. 8.22, в) величины касательных напряжений в полках значительно меньше величин 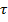, относящихся к одноименным точкам стенки. Этими небольшими напряжениями в полках пренебрегают и строят эпюру 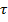только для стенки (см. рис. 8.22, г).

Для коротких и высоких балок величины касательных напряжений 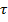соизмеримы с величинами нормальных напряжений 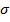. Поэтому для таких балок, где существенную роль играет деформация сдвига, проверяется условие прочности по касательным напряжениям 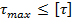, где 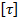– допускаемое касательное напряжение, выбираемое из нормативных документов.

С проверками прочности балок связаны гипотезы прочности.

Для простейший напряженных состояний условия прочности состоят в сопоставлении максимальных напряжений с величинами допускаемых напряжений:

а) для одноосного растяжения-сжатия (рис. 8.23, а)

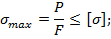
б) при сдвиге (срезе) на рис. 8.23, б

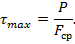
Рисунок 8.23 – Простейшие виды деформаций растяжения- сжатия(а), сдвига (б)

В то же время при поперечном изгибе балок в некоторых точках поперечных сечений возникают как нормальные, так и касательные напряжения. То есть напряженное состояние здесь будет двухосным (сложным). Поэтому вводятся так называемые гипотезы прочности, которые устанавливают признаки равнопрочности (эквивалентности) сложных напряженных состояний простейшим. Наиболее распространенными являются следующие гипотезы прочности:

а) гипотеза наибольших касательных напряжений (третья гипотеза прочности), согласно которой два напряженный состояния равнопрочны (простейшее и сложные), если максимальные касательные напряжения для них одинаковы. Проверка прочности проводится здесь по приведенным (эквивалентным) напряжениям:

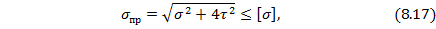
где 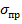– приведенные напряжения; 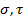– напряжения в поперечном сечении балки, где действует наибольший изгибающий момент .

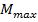б) энергетическая теория, называемая четвертой гипотезой прочности, соответствует условию:

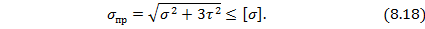
Условиями (8.17) и (8.28) можно установить наиболее напряженную точку по высоте сечения балки.

Так, для симметричной двутавровой балки (рис. 8.24) наиболее опасными точками по нормальным напряжениям будут т. 1, 5:

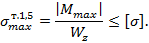
В этих точках нет касательных напряжений.

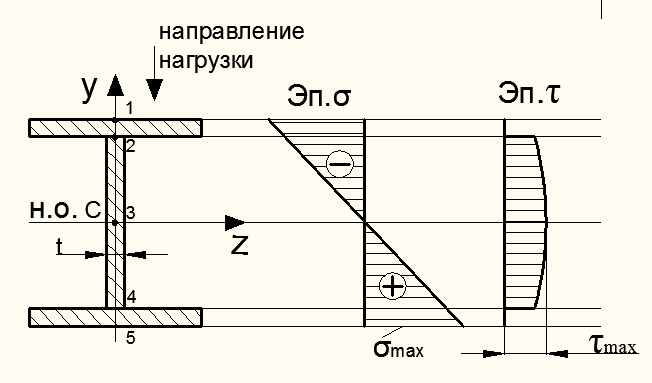Опасной точкой по касательным напряжениям будет т. 3, где действуют максимальные касательные напряжения, а нормальные напряжения равны нулю:

Рисунок 8.24 – К проверке прочности двутавровой балки

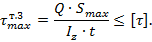
Однако есть точки т.т. 2, 4, где существуют и нормальные, и касательные напряжения. Для них и осуществляется проверка по приведенным напряжениям, например, по формуле (8.17):

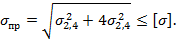
Здесь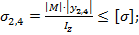

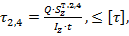
где перерезывающая сила определяется в том сечении, в котором действует 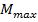; 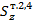– статический момент полки относительно н.о.