Как сравнивать результаты измерений.
Лабораторный практикум
Таблица соответствия лабораторных работ и разделов таблицы
«1.3. Содержание дисциплины»
| 1 семестр | |
| Раздел 1 | Лабораторная работа №1 |
| Раздел 2 | Лабораторная работа №2 |
| Раздел 4 | Лабораторная работа №3 |
| Раздел 5 | Лабораторная работа №4 |
| Раздел 7 | Лабораторная работа №5 |
| Раздел 11 | Лабораторная работа №6 |
| Раздел 11 | Лабораторная работа №7 |
| 2 семестр | |
| Раздел 12 | Лабораторная работа №8 |
| Раздел 13 | Лабораторная работа №9 |
| Раздел 14 | Лабораторная работа №10 |
| Раздел 14 | Лабораторная работа №11 |
| Раздел 16 | Лабораторная работа №12 |
| Раздел 16 | Лабораторная работа №13 |
| Раздел 16 | Лабораторная работа №14 |
Семестр
Введение. Ошибки измерений
Измерение – нахождение значения физической величины опытным путем с помощью средств измерений. Измерение, сделанное непосредственно каким-либо измерительным прибором, называется прямым (например, измерение диаметра цилиндра микрометром). Измерение, результат которого получается путем вычисления по формуле, называется косвенным измерением.
Очевидно, что никакое измерение не может быть выполнено абсолютно точно. В результате различных причин в ходе измерений неизбежно возникают погрешности. Они приводят к тому, что в результате измерений получают не истинное значение измеряемой величины, а его приблизительное значение. В задачу измерений входит не только определение значения самой величины, но также и оценка допущенных погрешностей.
Пусть измеряется некоторая величина, истинное или абсолютно точное значение которой обозначим через Х. В результате измерений получено значение этой величины, которое обозначим через х. Абсолютная погрешность или абсолютная ошибка Δх измеренной величины х определяется как модуль разности х и Х:
Δх = |х - Х| . (1)
Точность измерения лучше характеризуется не абсолютной, а так называемой относительной ошибкой:
ε = 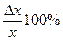 . (2)
. (2)
Поскольку истинное значение Х измеряемой величины, как правило, нам неизвестно, то вычисление абсолютной ошибки Δх по формуле (1) невозможно. Поэтому в теории ошибок разработаны различные методы расчета абсолютной ошибки для различных видов измерений и в понятие абсолютной ошибки вкладывается несколько иной смысл. Величина Δх определяет так называемый доверительный интервал, в котором с некоторой вероятностью (рассчитанной в теории ошибок) находится истинное значение измеряемой величины:
х – Δх < Х < х + Δх . (3)
Различают три типа погрешностей.
Грубые ошибки возникают в результате невнимания или усталости экспериментатора, а также при плохих условиях наблюдения. Они приводят к значениям измеряемой величины, резко отличающимся от остальных. Для устранения промахов следует соблюдать аккуратность и тщательность при проведении измерений.
Систематические или инструментальные ошибки Δхи– ошибки измерительных приборов, возникающие из-за несовершенства средств измерений. Эти ошибки определяются классом точности прибора или ценой деления прибора. Систематические погрешности могут быть обусловлены неисправностью измерительных приборов, например смещением нуля шкалы.
Случайные ошибки являются следствием действия факторов, влияние которых невозможно учесть. Таких факторов много, и роль их при каждом измерении не одинакова. Поэтому результаты повторных измерений физической величины Х, проведенных при использовании достаточно чувствительных и точных средств измерения, обычно отличаются друг от друга. В этом случае измеренное значение величины х находят как среднее арифметическое значение всех измерений, а ошибку Δхсл (ее называют случайной ошибкой) определяют методами математической статистики.
В школьном лабораторном практикуме обычно очень чувствительные и точные средства измерений не используются, случайные ошибки гораздо меньше инструментальных (результаты измерений одинаковые), поэтому для получения результата достаточно одного измерения.
Результат измерения записывается в виде:
Х = х ± Δхи [размерность] , (4)
где х – результат измерения; Δхи – инструментальная ошибка прибора. Такая запись результата означает, что истинное значение измеряемой величины находится в доверительном интервале (х – Δхи , х + Δхи ). Абсолютная ошибка округляется до одной или до двух значащих цифр. Численное значение результата измерений округляется так, чтобы его последняя цифра оказалась в том же разряде, что и последняя цифра ошибки. Например:
х =10, 281≈10,3; Δхи =0, 314≈0,3; Х = (10,3 ± 0,3 ) мм.
Точность прибора Δхи указана либо на самом приборе, либо в прилагаемом к нему паспорте. Если точность прибора неизвестна, то точность прибора определяется ценой наименьшего деления шкалы прибора (линейка, термометр, секундомер) или, если есть возможность более точного отсчета, половиной цены наименьшего деления шкалы прибора.
Для электроизмерительных приборов погрешность измерения характеризуется классом точности k прибора:
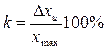 , (5)
, (5)
где Δхи - абсолютная инструментальная погрешность прибора; хmах - наибольшее значение измеряемой величины по шкале прибора. Значение класса точности электроизмерительного прибора указывается на лицевой стороне прибора или в его паспорте (знак % при этом не пишут). Существуют следующие классы точности: 0,1; 0,2; 0,5; 1; 1,5; 2,5; 4. Зная класс точности k прибора и величину хmах , определяют абсолютную ошибку измерения:
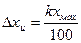 . (6)
. (6)
Как сравнивать результаты измерений.
1. Записать результаты измерений в виде (4).
2. Если доверительные интервалы не перекрываются, то результаты неодинаковые. Если доверительные интервалы хотя бы частично перекрываются, результаты считаются одинаковыми в пределах ошибок.
Если измерения косвенные, сначала рассчитывается относительная ошибка ε = 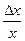 в долях единицы, а затем абсолютная ошибка по формуле Δх = ε х. Результат записывается в виде (4). Относительные ошибки ε для некоторых стандартных расчетных формул косвенных измерений приведены в таблице 1.
в долях единицы, а затем абсолютная ошибка по формуле Δх = ε х. Результат записывается в виде (4). Относительные ошибки ε для некоторых стандартных расчетных формул косвенных измерений приведены в таблице 1.
Таблица 1.
