Условие корней многошаговых методов решения задачи Коши

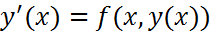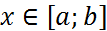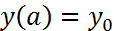Рассмотрим задачу Коши , (1) и (2). На 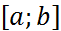введем сетку 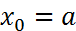, , 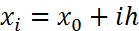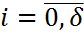. Рассмотрим многошаговый метод, определяемый формулой

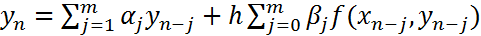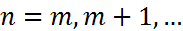, (3). Для реализации вычислений по формуле (3) в начале необходимо найти разгонные значения. 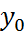берется из (2), 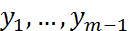находящееся одинаковым методом(например методом Рунге-Кутта).

Если 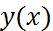– точное решение задачи (1),(2), то при подстановке его в (3) будем иметь: 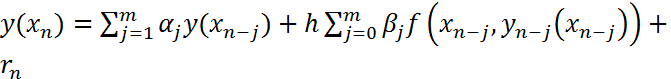, (4)

Вычитая из (3)-(4) для погрешности 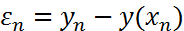будем иметь уравнения: 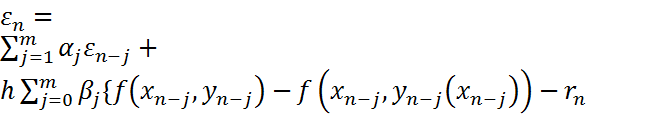(5).

Обозначим

,

.

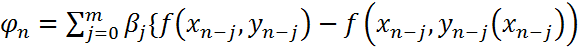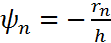Теперь (5) перепишем в виде

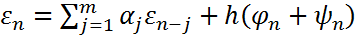(6). К (6) добавим равенство 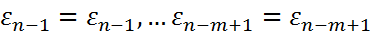(7).

Равенство (6),(7) запишем в следующем виде

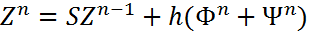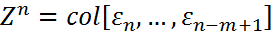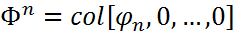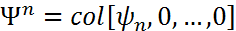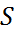(8), где , , а - матрица Фробениуса.

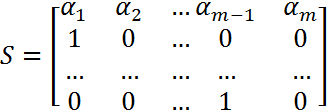
Отметим, что начальное условие для (8) 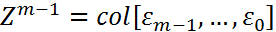, т.е. компоненты начального вектора 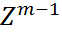есть погрешности, полученные при вычислении разгонных значений одношаговым методом. Уравнение (8) называется канонической формой многошагового метода (3) для погрешностей. Рассмотрим характеристический многочлен 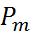матрицы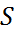 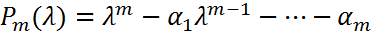, где 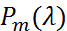называется характеристическим многочленом метода (3).

Обозначим через 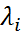- корни многочлена .

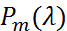Рассмотрим влияние корней 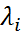на устойчивость метода (3). Предположим, что некоторые 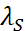удовлетворяют условию 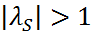. Пусть 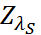собственный вектор матрицы 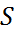, отвечающий собственному значению 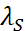. Предположим, что начальный вектор 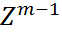уравнения (8) таков, что 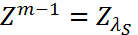. Тогда, в случае однородного уравнения (8) будем иметь: 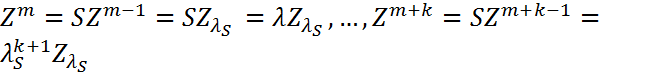. Поскольку 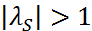, то в этом случае общее решение неоднородного уравнения (8) будет содержать быстро растущее по норме слагаемое. А значит, вычисление по (8) будет неустойчивыми, т.е. сильно чувствительными к начальной погрешности. Пусть теперь 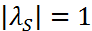, но кратность 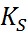числа 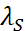как корня характеристического уравнения 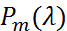больше 1, т.е. 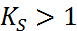. Для хар-ой матрицы

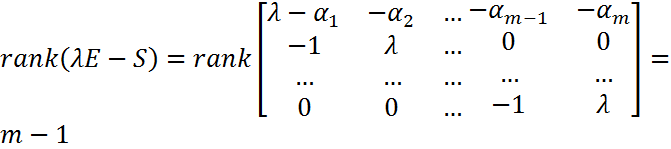при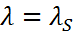

(строки со второй по линейно независимы). Значит, в канонической форме Жордана матрица 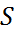будет содержать Жорданову клетку порядка больше 1. Например, если 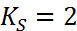, такой клеткой будет 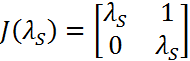. Очевидно, что 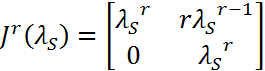, а значит, общее решение уравнения (8) также будет содержать быстро растущее по норме слагаемые. Из всего этого следует следующее утверждение.

Теорема. Для того, чтобы многошаговый метод (3) был устойчивый, необходимо, чтобы все корни характеристического многочлена 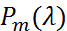метода (3) не лежали за пределами единичного круга, а среди корней, лежащих на границе единичного круга, не было кратных.

Опр. Если корни характеристического уравнения (3) удовлетворяет условию теоремы, то говорят, что метод (3) удовлетворяет условию корней.

Лемма. Пусть многошаговый метод (3) удовлетворяет условию корней. Тогда существует векторная норма 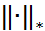, что для подчиненной матричной нормы выполняется .

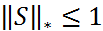Док-во. Пусть 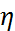некоторая положительное число. Если 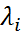собственные значения матрицы 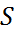, то 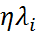- собственные значения матрицы 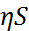. Пусть преобразование 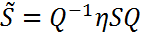приводит матрицу 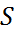к канонической форме Жордана. Тогда каждая строка матрицы 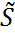будет иметь вид: 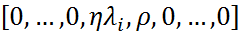, где число 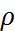принимает значение 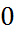или 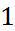в зависимости от номера строки и кратности числа 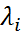. Тогда каждая строка матрицы 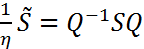имеет вид: 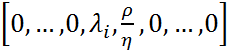. Пусть кратность корня 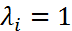. Тогда в строках матрицы 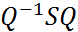, содержится число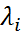 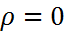. Поэтому сумма модулей элементов этих строк равна 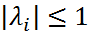. Пусть кратность корня 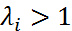. Тогда в силу условия корней 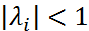, а значит при 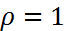, сумма модулей элементов строки меньше либо равна 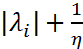и 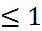при достаточно большом .

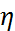Таким образом, что 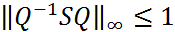(9).

Определим вектор норму 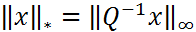. Тогда имеем оценку

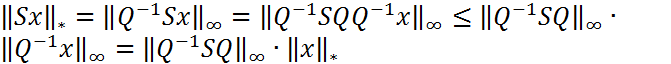(10).

Согласно определению подчиненной матричной нормы.

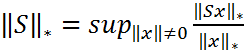Поэтому из (10) следует, что 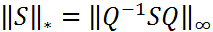, а из (9) следует что 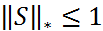. Доказано.