Основные уравнения динамики жидкости

Литература

Основная

1. Лапшев, Н. Н. Гидравлика: учебник. – М.: Академия, 2012. – 272 с

Дополнительная

1. Лойцянский Л.Г. Механика жидкости и газа / Л.Г. Лойцянский. М.: Наука, 1978.

2. Альтшуль А.Д. Гидравлика и аэродинамика / А.Д. Альтшуль, Л.С. Животовский, Л.П. Иванов. М.: Стройиздат, 1975.

3. Большаков В.А. Справочник по гидравлике / В.А. Большаков,
Ю.М. Константинов. Киев: Вища школа, 1984.

4. Сборник задач по гидравлике / под ред. В.А. Большакова. 4-е изд. Киев: Вища школа, 1979.

5. Справочник по гидравлическим расчетам / под ред. П.Г. Киселева.
4-е изд. М.: Энергия, 1972.

6. Гидравлика и газовая динамика: методические указания и контрольные вопросы / под ред. Е.В. Балахонцева, Л.А. Владиславлева. М.: Высшая школа, 1980.

7. Киселев П.Г. Гидравлика / П.Г. Киселев. М.: Энергия; 1980.

8. Штеренлихт Д.В. Гидравлика / Д.В. Штеренлихт. М.: Стройиздат, 1984.

9. Емцев Б.Т. Техническая гидромеханика / Б.Т. Емцев. М.: Машиностроение, 1978.

Методическая литература:

1. Борисенко, О. А. (СевКавГТУ). Гидравлика : учебное пособие (курс лекций) / О. А. Борисенко; Сев.-Кав. гос. техн. ун-т. – Ставрополь : СевКавГТУ, 2010. – 133 с.

2. Калиниченко, М.Ю. Лабораторный практикум для проведения лабораторных работ по дисциплинам «Гидравлика», «Гидравлика и гидропневмопривод», «Механика жидкости и газа», «Прикладная гидродинамика», «Инженерные системы зданий и сооружений (водоснабжение и водоотведение с основами гидравлики)» – Ставрополь.: СКФУ, 2016, – 72 с.

3. Калиниченко, М.Ю. Практикум для проведения практических занятий по дисциплинам «Гидравлика», «Гидравлика и гидропневмопривод», «Механика жидкости и газа», «Прикладная гидродинамика», «Инженерные системы зданий и сооружений (водоснабжение и водоотведение с основами гидравлики)» – Ставрополь.: СКФУ, 2016, – 82 с.

ФИЗИЧЕСКИЕ СВОЙСТВА ЖИДКОСТЕЙ И ГАЗОВ

Определение жидкости. Силы, действующие на жидкость (массовые и поверхностные). Плотность жидкости. Вязкость. Закон Ньютона для тре­ния в жидкости. Температурное расширение и сжимаемость жидкости. Поверхностное натяжение. Модель идеальной жидкости.

Методические указания

По своим физическим свойствам жидкости занимают промежуточное положение между твердыми телами и газами. Жидкость весьма мало изме­няет свой объем при изменении давления или температуры, в этом отно­шении она сходна с твердым телом. Жидкость обладает текучестью, бла­годаря чему она не имеет собственной формы и принимает форму того со­суда, в котором находится. В этом отношении жидкость отличается от твердого тела и имеет сходство с газом. Свойства жидкостей и их отличие от твердых тел и газов обусловливаются молекулярным строением. Следу­ет уяснить, каким образом особенности молекулярного строения влияют на физические свойства жидкости.

Покоящаяся жидкость подвержена действию двух категорий внешних сил: массовых и поверхностных. Массовые силы пропорциональны массе жидкости или для однородных жидкостей – ее объему. Следует знать, какие силы относятся к массовым (объемным) и к поверхностным силам, какие силы называются внешними и какие внутренними.

В покоящейся жидкости может существовать только напряжение сжа­тия, т. е. давление. Необходимо четко представлять разницу между поня­тиями среднего гидростатического давления, гидростатического давления в точке, выраженных в единицах напряжения, и понятием суммарного гид­ростатического давления на поверхность, выраженного в единицах силы.

В гидравлике при изучении законов равновесия и движения широко пользуются различными физическими характеристиками жидкости (на­пример, плотность). Студенту нужно уметь определять основные физиче­ские характеристики жидкости, знать единицы этих характеристик.

Следует также рассмотреть основные физические свойства капельных жидкостей: сжимаемость, тепловое расширение, вязкость и др.

Вязкостью называется свойство жидкости оказывать сопротивление относительному перемещению слоев, вызывающему деформацию сдвига. Это свойство проявляется в том, что в жидкости при ее движении возника­ет сила сопротивления сдвигу, называемая силой внутреннего трения. При прямолинейном слоистом движении жидкости сила внутреннего трения 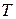между перемещающимися один относительно другого слоями с площадью соприкосновения 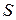определяется законом Ньютона:

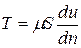или .

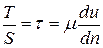Динамический коэффициент вязкости 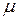не зависит от давления и от характера движения, а определяется лишь физическими свойствами жид­кости и ее температурой. Как видно, сила 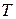и касательное напряжение 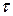пропорциональны градиенту скорости 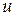по нормали 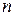к поверхности тре­ния 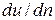, который представляет собой изменение скорости жидкости в направлении нормали на единицу длины нормали.

Учет сил вязкости значительно осложняет изучение законов движения жидкости. С другой стороны, капельные жидкости незначительно изменя­ют свой объем при изменении давления и температуры. В целях упроще­ния постановки задач и их математического решения создана модель иде­альной жидкости. Идеальной жидкостью называется воображаемая жид­кость, которая характеризуется полным отсутствием вязкости и абсолют­ной неизменяемостью объема при изменении давления и температуры. Переход от идеальной жидкости к реальной осуществляется введением в конечные расчетные формулы поправок, учитывающих влияние сил вязко­сти и полученных главным образом опытным путем. При изучении гидро­динамики следует проследить особенности перехода от идеальной жидкости к реальной.

В гидравлике жидкость рассматривается как сплошная среда (конти­нуум), т.е. среда, масса которой распределена по объему непрерывно. Это позволяет рассматривать все характеристики жидкости (плотность, вяз­кость, давление, скорость и др.) как функции координат точки и времени, причем в большинстве случаев эти функции предполагаются непрерывными.

Контрольные вопросы

1. Что называют жидкостью? Каковы ее отличительные признаки?

2. Как определяют плотность жидкости? Указать ее наименование в системе СИ.

3. Что называют коэффициентом объемного сжатия? Пояснить его связь с модулем упругости жидкости.

4. Как определяется коэффициент температурного расширения? Ука­зать его наименование и численные значения для воды.

5. Сформулируйте и запишите закон вязкого трения Ньютона с ука­занием физического смысла всех входящих величин.

6. Каковы наименования коэффициентов динамической и кинемати­ческой вязкости в системе СИ? Какими приборами измеряется вязкость жидкостей?

7. Как зависят коэффициенты динамической и кинематической вяз­кости от давления и температуры у капельных и газообразных жидкостей? Пояснить их с точки зрения молекулярного строения жидкостей и газов.

8. Объясните явление капиллярности в трубках малого диаметра. Как подсчитать величину капиллярного поднятия или опускания в трубке малого сечения?

9. С какой целью в гидравлике вводится понятие об идеальной жид­кости? Чем отличается идеальная (гипотетическая) жидкость от реальной жидкости?

10. Приведите уравнения состояния для жидкостей и газов.

ГИДРОСТАТИКА

Свойства гидростатического давления. Дифференциальные уравнения равновесия (уравнение Эйлера). Интегрирование уравнений Эйлера. Основное уравнение гидростатики (1-я и 2-я формы). Поверхности равного давления. Закон Паскаля. Приборы для измерения давления. Сила давле­ния жидкости на плоские и криволинейные поверхности. Закон Архимеда.

Методические указания

Два свойства гидростатического давления обусловлены тем, что по­коящаяся жидкость не воспринимает касательных и растягивающих уси­лий. Знание этих свойств позволяет понять физический смысл формул ста­тического силового воздействия жидкости на твердые тела.

Наиболее общими уравнениями гидростатики являются дифферен­циальные уравнения Эйлера, устанавливающие связи между массовыми и поверхностными силами, действующими в жидкости. При изучении этих уравнений следует усвоить физический смысл всех входящих в них вели­чин. Эти уравнения позволяют просто и быстро решать задачи как в случае

абсолютного покоя жидкости, когда на жидкость из массовых сил действу­ет только сила тяжести, так и в случае относительного покоя, когда к силе тяжести присоединяются силы инерции. В случае действия на жидкость одной лишь силы тяжести интегрирование уравнений Эйлера дает основ­ное уравнение гидростатики:

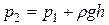
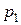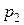где и – давление в точках 1 и 2; 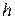– глубина погружения точки 2 относительно точки 1; 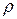– плотность жидкости.

В зависимости от способа отсчета различают абсолютное, избыточ­ное (манометрическое) и вакуумметрическое давление. Следует знать взаимосвязь этих величин.

В уравнении точка 1 может лежать на свободной поверхности жидко­сти. При этом давление 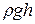будет избыточным только в том случае, когда давление на свободную поверхность равно атмосферному.

Весьма важными понятиями в гидравлике являются пьезометрическая высота и гидростатический напор. Пьезометрическая высота выражает в метрах столба жидкости избыточное (или абсолютное) давление в рас­сматриваемой точке жидкости. Гидростатический напор равен сумме гео­метрической 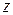и пьезометрической 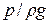высот. Для всех точек данного объема покоящейся жидкости гидростатический напор относительно вы­бранной плоскости сравнения есть постоянная величина.

Воздействие жидкости на плоские и криволинейные поверхности наглядно отражается эпюрами давления. Площадь (объем) эпюры дает величину силы давления, а центр тяжести этой площади (объема) точку приложения силы давления. Аналитическое рассмотрение задачи позволя­ет получить весьма простые расчетные формулы. В случае плоской по­верхности любой формы величина силы гидростатического давления равна смоченной площади этой поверхности, умноженной на гидростатическое давление в центре тяжести площади. Точка приложения силы гидростати­ческого давления (центр давления) лежит всегда ниже центра тяжести (за исключением давления на горизонтальную плоскость, когда они совпа­дают). Следует указать, что формула для определения координаты центра давления дает точку приложения силы только гидростатического давления без учета давления на свободную поверхность (см. вывод формулы в любом учебнике гидравлики).

Для криволинейных цилиндрических поверхностей обычно определяют горизонтальную и вертикальную составляющие полной силы гидростати­ческого давления. Определение вертикальной составляющей связано с по­нятием «тела давления», которое представляет собой действительный или воображаемый объем жидкости, расположенный над цилиндрической поверхностью. Линия действия нормальной составляющей проходит через центр давления вертикальной проекции криволинейной поверхности, а ли­ния действия вертикальном составляющей – через центр тяжести тела давления.

При изучении этого раздела студенту полезно рассмотреть несколько конкретных примеров построения тел давления для цилиндрических по­верхностей, определить самостоятельно вертикальную и горизонтальную составляющие силы давления, точки их приложения и результирующую силу.

Необходимо рассмотреть давление жидкости на стенки труб и резер­вуаров и расчетные формулы для определения толщины их стенок.

Контрольные вопросы

1. Что такое массовые и поверхностные силы?

2. Что называется гидростатическим давлением в точке, и какими двумя свойствами оно обладает?

3. Какой вид имеют дифференциальные уравнения равновесия жид­кости (уравнение Эйлера)? Каков физический смысл входящих в них величин?

4. Вывести зависимость для определения полного гидростатического давления в данной точке.

5. Как формулируется закон Паскаля? Какое применение находит этот закон в технике?

6. Как определяется сила гидростатического давления жидкости на плоскую фигуру? Что такое центр давления и как находится глубина его погружения?

7. Поясните, что собой представляет эпюра гидростатического давления? Изобразите графически изменение гидростатического давления вдоль вертикальной стенки и по дну сосуда, заполненного жидкостью.

8. Как определяется результирующая сила давления жидкости на криволинейную поверхность?

9. Что такое тело давления? Какие бывают тела давления?

10. Вывести и сформулировать закон Архимеда.

КИНЕМАТИКА

Виды движения жидкости. Основные понятия кинематики жидкости: линия тока, трубна тока, струйка, живое сечение, расход. Поток жидкости. Средняя скорость. Уравнение постоянства расхода (уравнение неразрыв­ности). Изменение средней скорости вдоль потока.

Методические указания

Кинематика изучает движение жидкости вне зависимости от сил, дей­ствующих на нее. Изучая эту тему, студент должен ясно представлять себе струйную модель потока жидкости, основой которой является элементар­ная струйка.

При изучении этого раздела студент должен понять, как происходит движение частицы жидкости и чем это движение отличается от движения твердого тела. Частицы жидкости участвуют в поступательном, враща­тельном и деформационном движении.

Одним из основных уравнений кинематики является уравнение посто­янства расхода (уравнение неразрывности), которое для плавно изменяю­щегося движения может быть представлено в виде 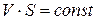(вдоль по­тока), откуда для двух сечений 1 и 2 получим 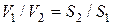, т.е. средние скорости потока обратно пропорциональны площадям живых сечений.

Контрольные вопросы

1. Что такое линия тока и траектория частицы жидкости? Когда они совпадают?

2. Что такое элементарная струйка, и какими свойствами она обладает при установившемся движении жидкости?

3. Какое движение жидкости называется установившимся и неуста­новившимся? В чем их различие? Привести не менее четырех примеров, иллюстрирующих эти виды движения.

4. Что называется равномерным и неравномерным движением жид­кости? Привести не менее двух примеров для каждого из этих видов.

5. Дайте определения и укажите наименования единиц в системе СИ следующих гидравлических величин и характеристик: живое сечение, смо­ченный периметр, гидравлический радиус, расход.

6. Что такое расход потока и как по расходу можно определить среднюю скорость движения жидкости в сечении потока?

7. Как Вы представляете себе модель потока жидкости?

8. Выведите уравнение неразрывности для элементарной струйки невязкой жидкости.

ОСНОВНЫЕ УРАВНЕНИЯ ДИНАМИКИ ЖИДКОСТИ

Дифференциальные уравнения движения идеальной жидкости. Урав­нение Бернулли для установившегося движения идеальной жидкости. Гео­метрический и энергетический смысл уравнения Бернулли. Уравнение Бернулли для потока реальной жидкости. Коэффициент Кориолиса. Общие понятия о потерях. Виды гидравлических потерь.

Методические указания

Важным уравнением в гидравлике, применяемым на практике, явля­ется уравнение Бернулли:

,

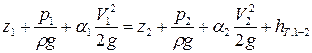где 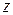– геометрический напор; возвышение рассматриваемой точки (точки с давлением 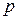) данного живого сечения над произвольно выбранной гори­зонтальной плоскостью сравнения 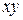или 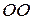; мера воздействия на поток силы тяжести; удельная потенциальная энергия положения относительно Земли, т.е. потенциальная энергия поля земного притяжения; 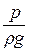– пьезометрический напор; возвышение уровня в пьезометрической трубке над точкой, имеющей ординату 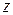; мера («пьезометрический» значит «давление меряющий») воздействия на поток силы давления: удельная потенциальная энергия давления; 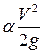– скоростной напор; возвышение уровня в трубке Пито, нижний открытый конец которой загнут против течения, над уров­нем в пьезометре; мера воздействия на поток конвективной силы инерции; удельная кинетическая энергия; высота взлета струи, выпущенной верти­кально вверх со скоростью 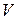; 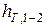– потерянный напор; понижение линии энергии (механической) на участке между сечениями 1 и 2, для которых составляется уравнение Бернулли; мера воздействия сил трения; удельная механическая энергия, перешедшая в тепловую на участке 1 – 2вследствие работы сил трения.

Уравнение Бернулли надо не только хорошо знать, понимать, но и уметь им пользоваться для решения практических задач, уметь составлять его для различных конкретных случаев, что достигается только практикой. Работая с уравнением Бернулли, полезно руководствоваться следующими указаниями:

1) уравнение Бернулли составляется для двух живых, т. е. нормальных к направлению скорости, сечений; эти сечения должны располагаться на прямолинейных участках потока;

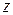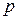2) одно из этих сечений следует брать там, где требуется определить или , или , или 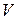; другое сечение рекомендуется брать там, где 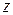, 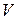и 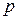известны;

3) нумеровать расчетные сечения следует так, чтобы жидкость двига­лась от 1-го ко 2-му; в противном случае должен быть изменен на обрат­ный знак ;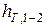

4) горизонтальную плоскость сравнения желательно по высоте совме­щать с тем из двух расчетных сечений, которое располагается ниже; тогда один из 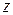выпадет из уравнения, а второй будет величиной положительной;

5) последний член уравнения должен учитывать все потери напора между расчетными сечениями.

Контрольные вопросы

1. Напишите дифференциальные уравнения движения идеальной жид­кости (уравнения Эйлера) и объясните физический смысл входящих в них членов.

2. Как записывается уравнение Бернулли для элементарной струйки идеальной жидкости? Каков геометрический и энергетический смысл каждого слагаемого в уравнении Бернулли?

3. Запишите уравнение Бернулли для элементарной струйки реальной (вязкой) жидкости. Каков геометрический и энергетический смысл каждого слагаемого в уравнении Бернулли?

4. Как записывается уравнение Бернулли для потока реальной жидко­сти? Пояснить геометрический и энергетический смысл его членов.

5. В чем состоит отличие уравнения Бернулли для элементарной струйки реальной жидкости от уравнения Бернулли потока реальной жидкости?

6. Каков физический смысл коэффициента Кориолиса (а) в уравнении Бернулли для потока реальной жидкости?

7. Укажите условие применения уравнения Бернулли для потока.

8. С какой целью вводится понятие о плавной изменяемости потока при выводе уравнения Бернулли для потока реальной жидкости?

9. Запишите уравнение Бернулли для двух сечений равномерного потока (например, в трубе) реальной жидкости, ось которого горизонтальна. Как изменяется давление по длине потока?

10. Может ли изменяться знак пьезометрического уклона от положи­тельного до отрицательного? В каких случаях? Может ли быть отрица­тельным гидравлический уклон?