Тестирование и оптимизация.
Изначально программа тестировалась на симметричных матрицах с диагональным преобладанием, то есть при построении матрицы на главную диагональ прибавлялась 1000, что давало очень хорошую сходимость при заданной точности 0,001 у всех четырёх методов. При этом было видно, что наихудшую скорость сходимости дает метод минимальных поправок, наилучшую – метод сопряжённых градиентов. Разница в скорости сходимости становилась заметна, при размерности матрицы больше чем 200х200 элементов, что видно на графике (см. рис.7)
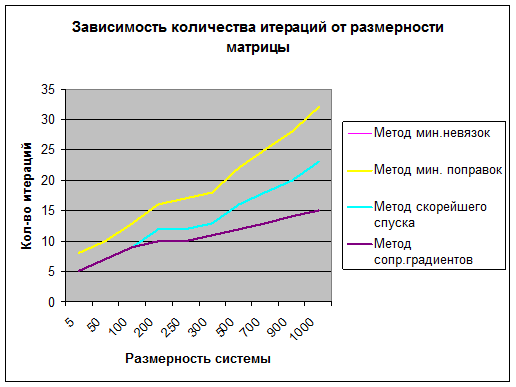
Рис.7 Зависимость количества итераций от размерности матрицы.
Для более наглядной демонстрации работы вариационных методов в программу была добавлена возможность генерировать матрицы без диагонального преобладания, а также с диагональным преобладанием, заданным пользователем. В результате были сделаны следующие наблюдения: при отсутствии диагонального преобладания метод минимальных невязок очень медленно сходится (за несколько сотен тысяч итераций), при этом он сходится только для точности не меньше 0,01 и матриц размерностью не больше 50. Аналогичная ситуация наблюдается с методами минимальных поправок и скорейшего спуска. Если задавать небольшое диагональное преобладание, то скорость сходимости увеличивается. На рисунке 8 показано, как изменяется количество итераций в зависимости от диагонального преобладания при размерности матрицы 10х10 и точности, равной 0,01.
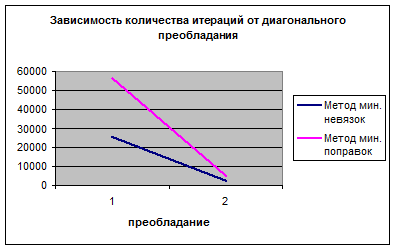
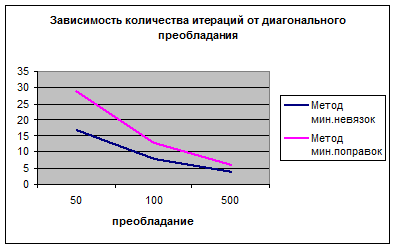
Рис.8 Зависимость количества итераций от диагонального преобладания
Что касается метода сопряжённых градиентов, то диагональное преобладание незначительно влияет на скорость его сходимости, так, в случае матрицы 10х10 элементов без диагонального преобладания и при точности, равной 0,01, метод минимальных невязок сошёлся за 25329 итераций, а метод сопряжённых градиентов – за 11 итераций.
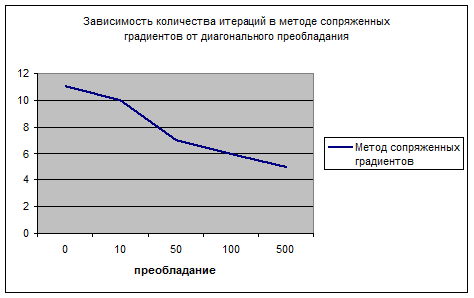
Рис. 9 Зависимость количества итераций в методе сопряженных градиентов от диагонального преобладания
Таким образом, из всех исследованных методов метод сопряжённых градиентов является наиболее эффективным.
Для хранения матриц и векторов были использованы динамические массивы, что ускоряет работу программы и позволяет пользователю практически неограниченно задавать размерность матрицы системы. Также в методе минимальных поправок матрично-матричное умножение заменено матрично-векторным, что позволяет значительно снизить время, затрачиваемое на вычисления.
Выводы
В ходе выполнения данной курсовой работы были исследованы такие методы решения СЛАУ, как метод минимальных невязок, метод минимальных поправок, метод скорейшего спуска и метод сопряженных градиентов. Составлены алгоритмы решения СЛАУ перечисленными методами, которые в дальнейшем были использованы для написания программы. Сравнение решений, полученных с помощью данных методов, с точным решением показало состоятельность методов. В ходе исследования сходимости в случае матриц с диагональным преобладанием, было обнаружено, что скорость сходимости метода сопряжённых градиентов наибольшая. В случае матриц без диагонального преобладания метод сопряжённых градиентов сходится значительно быстрее всех остальных методов, причём разница в сходимости может составлять десятки тысяч раз. Методы минимальных невязок, минимальных поправок и скорейшего спуска применимы только в случае матриц с хорошим диагональным преобладанием. В отличие от этих методов, метод сопряжённых градиентов сходится для любых симметричных матриц, при этом он даёт настолько лучшую сходимость по сравнению с остальными методами, что это делает его самым эффективным среди рассмотренных методов.
