Теоретичні відомості про невизначений інтеграл та методи інтегрування
Означення. Функція F(x) називається первісною для функції f(x), якщо f¢(x)=F(x).
Означення. Невизначеним інтегралом від функції f(x) називається сукупність усіх первісних цієї функції.
Використовується позначення 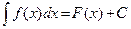 , де f(x)dx - підінтегральний вираз, а C - стала інтегрування.
, де f(x)dx - підінтегральний вираз, а C - стала інтегрування.
З геометричного погляду невизначений інтеграл – це сукупність (сім’я) ліній F(x)+C
Основні формули інтегрування
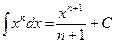 (n¹-1) , у тому числі
(n¹-1) , у тому числі
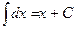 ;
;
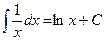 ;
;
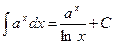 , у тому числі
, у тому числі 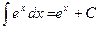 ;
;
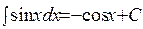 ;
;
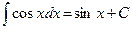 ;
;
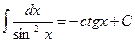 ;
;
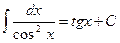 ;
;
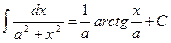 , у тому числі
, у тому числі 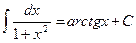 ;
;
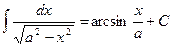 , у тому числі
, у тому числі 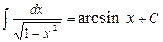 ;
;
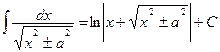 .
.
Із означення невизначеного інтеграла випливають такі властивості інтегрування:
1) 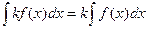 ;
;
2) 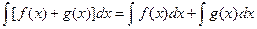 ;
;
3) 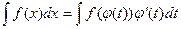 (метод заміни змінних, метод підстановки);
(метод заміни змінних, метод підстановки);
4) 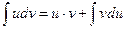 (інтегрування частинами).
(інтегрування частинами).
Задача 1. Обчислити невизначені інтеграли методом підстановки:
а) 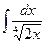 ; б)
; б) 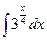 ; в)
; в) 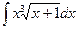 ; г)
; г) 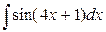 ;д)
;д) 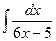
Задача2. . Обчислити невизначені інтеграли методом інтегрування частинами:
а) 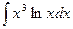 ; б)
; б) 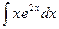 ; в)
; в) 
Питання для самоконтролю знань, умінь
1. Що таке первісна функції? Необхідна умова існування первісної.
2. Що таке невизначений інтеграл?
3. Властивості невизначеного інтегралу.
4. Правила інтегрування
5. Метод заміни змінної (підстановки) обчислення невизначених інтегралів.
6. Метод інтегрування частинами у невизначеному інтегралів.
Висновок. _________________________________________________________
____________________________________________________________________
Перевірив викладач ___________ Оцінка ___________ Дата___________
Виконаємо самостійно
В - 1 В - 2
1. Знайти інтеграли методом безпосереднього інтегрування.
а) 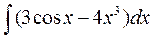 а)
а) 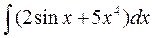
б) 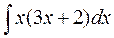 б)
б) 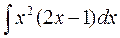
2. Знайти інтеграли методом заміни.
а) 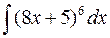 а)
а) 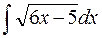
б) 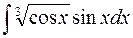 б)
б) 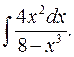
3. Знайти інтеграли методом інтегрування частинами.
а) 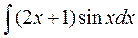 а)
а) 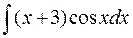
В - 3 В - 4
1. Знайти інтеграли методом безпосереднього інтегрування.
а) 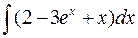 а)
а) 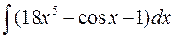
б) 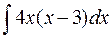 б)
б) 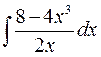
2. Знайти інтеграли методом заміни.
а) 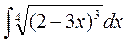 а)
а) 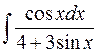
б) 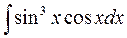 б)
б) 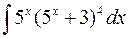
3. Знайти інтеграли методом інтегрування частинами.
а) 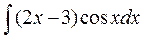 а)
а) 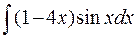
В - 5 В - 6
1. Знайти інтеграли методом безпосереднього інтегрування.
а) 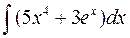 а)
а) 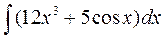
б) 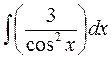 б)
б) 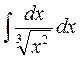
2. Знайти інтеграли методом заміни.
а) 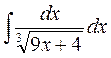 а)
а) 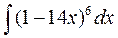
б) 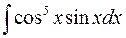 б)
б) 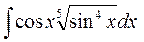
3. Знайти інтеграли методом інтегрування частинами.
а) 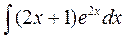 а)
а) 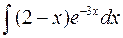
В - 7 В - 8
1. Знайти інтеграли методом безпосереднього інтегрування.
а) 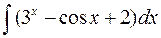 а)
а) 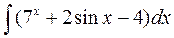
б) 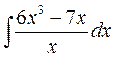 б)
б) 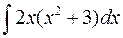
2. Знайти інтеграли методом заміни.
а) 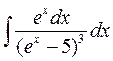 а)
а) 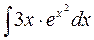
б) 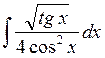 б)
б) 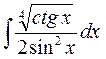
3. Знайти інтеграли методом інтегрування частинами.
а) 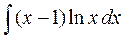 а)
а) 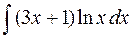
ПРАКТИЧНА РОБОТА № 14
Тема. Розв’язування задач на обчислення визначених інтегралів частинами та заміною змінних
Мета роботи: Навчитись обчислювати визначені інтеграли частинами та заміною змінних.
Наочне забезпечення та обладнання:
1. Інструкційні картки
2. Приклади задач
3. Роздаткові матеріали: опорні конспекти “Основні формули інтегрування”
4. Обчислювальні засоби: калькулятор.

Теоретичні відомості про правила інтегрування та застосування визначеного інтегралу.
Визначений інтеграл та методи його обчислення
