Закон непрерывности магнитных силовых линий.

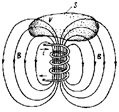Экспериментально было обнаружено, что силовые линии векторного поля магнитной индукции В всегда замкнуты в пространстве независимо от того, создается ли поле постоянными магнитами или катушками с током.

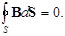Для математического описания этого факта удобно представить себе силовые линии магнитного поля как воображаемые линии скоростей движения частиц несжимаемой жидкости. Расположим внутри области существования магнитного поля произвольный объем V, ограниченный поверхностью S. Если силовые линии замкнуты, то поток втекающей жидкости в точности равен потоку, вытекающему из объема. Таким образом,

Откуда получим соотношение, относящееся к бесконечно малой окрестности выбранной точки пространства: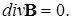

Эти две формулы математически выражают закон неразрывности магнитных силовых линий в интегральной и дифференциальной форме соответственно.

Эквивалентной формулировкой рассмотренного закона служит утверждение о том, что векторное поле В нигде не имеет источников. Другими словами, никаких магнитных зарядов в природе не существует. Если, по аналогии с электрическим током, мысленно допустить существование некоторого магнитного тока, то такой гипотетический ток не имеет прямого физического смысла, хотя иногда может оказаться весьма полезным при проведении расчетов.

Векторные поля без источников, т. е. с нулевой дивергенцией, в физике и математике называют соленоидальными полями.

Закон полного тока.

В начале XIX в. датский физик Эрстед экспериментально открыл принципиально важный факт: протекание электрического тока по проводнику сопровождается возникновением в окружающем пространстве магнитного поля. Опыты Эрстеда позволили французскому ученому Амперу сформулировать теоретическое положение, которое называют законом полного тока или законом Ампера.

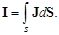
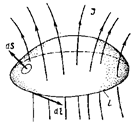Пусть имеется воображаемый замкнутый контур L на который опирается кусок гладкой поверхности S. Зададим на этом контуре направление обхода таким образом, чтобы с конца вектора элементарной площадки dS движение вдоль контура наблюдалось в направлении против стрелки часов. Пусть поверхность S пронизывается некоторой системой токов. Эти токи могут быть дискретны- ми (совокупность отдельных проводников) или распределенными непрерывно (подобно электронному потоку). Не указывая заранее физической природы этих токов, будем для определенности полагать, что они распределены в пространстве непрерывно с некоторой плотностью J. Тогда полный ток, пронизывающий контур,

Закон полного тока формулируется так: циркуляция вектора напряжен- ности магнитного поля Н по контуру L равна полному току, т. е.

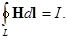
Это соотношение выражает закон полного тока в интегральной форме. Чтобы получить дифференциальную форму этого закона, т. е. связать плотность полного тока с напряженностью магнитного поля, следует использовать теорему Стокса. В результате получим

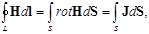
откуда ввиду произвольности выбранного контура получаем

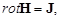равенство

которое представляет закон полного тока в дифференциальной форме.

Используя интегральную формулировку закона полного тока, можно решать некоторые простые задачи, связанные с нахождением магнитного поля заданных токов.

Ток смещения.

Известно, что переменный электрический ток способен протекать по замкнутой цепи, содержащей конденсатор, несмотря на то, что в пространстве между обкладками отсутствуют какие-либо носители электрического заряда. Можно предположить, что в этой области протекает некий ток, по своей природе принципиально отличный от тока проводимости. Этот ток называют током смещения.

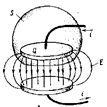
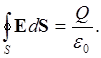Рассмотрим цепь с конденсатором. Одна из обкладок конденсатора окружена воображаемой замкнутой поверхностью S. Будем считать, что между обкладками находится вакуум.

По закону Гаусса,

Ток в цепи i связан с зарядом Q выделенной обкладки:

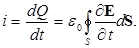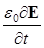Отсюда видно, что величина

имеет размерность плотности тока, который и назван током смещения.

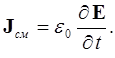Итак, плотность этого тока

Максвелл предложил ввести величину и плотность тока проводимости в правую часть формулы закона полного тока. При этом устанавливалась внутренняя взаимосвязь электрического и магнитного полей. Изменение во времени электрического поля в какой-либо точке пространства приводит к возникновению тока смещения в окрестности этой точки. Ток смещения, в свою очередь, вызывает появление переменного магнитного поля.