Построение линии пересечения многогранников ( 2-я позиционная задача)
1. Выполнить комплексный чертеж каких-либо двух пересекающихся многогранников;
2. Построить линию их пересечения и определить видимость.
3. Ответить на следующие вопросы:
а) Какая линия получилась в результате пересечения
б) Какие ее точки являются опорными;
в) По какой схеме определялись опорные точки;
г) Какие случаи возможны при пересечении двух многогранников
Даны прямая треугольная призма, стоящая на плоскости H, и произвольно расположенная треугольная пирамида. Построить линию пересечения заданных поверхностей
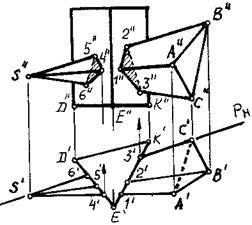
Ребра призмы обозначим одной буквой (D, E, K), а пирамиды — двумя буквами (SA, SB, SC).
Задачу сводим к определению точек встречи ребер пирамиды с гранями призмы. Особенность этого примера — грани призмы являются проецирующими плоскостями (ее ребра перпендикулярны к плоскости Н). Горизонтальные проекции 1-2-3 и 4-5-6 линий пересечения уже имеются, они совпадают с горизонтальной проекцией самой призмы. С помощью линий связи находят фронтальные проекции этих точек на соответствующих ребрах. В результате получают две замкнутые ломаные линии: 1”-2”-3” у входа и 4”-5”-6” у выхода. Отрезки 2”-3” и 5”-6” этих линий невидимые, так как они лежат на задней грани пирамиды.
Экзаменационный билет №_19
Соосными называются поверхности вращения, имеющие общую ось
Особое место при пересечении соосных поверхностей вращения отводится сферам, свойства которых используются в дальнейшем при построении линии пересечения кривых поверхностей.
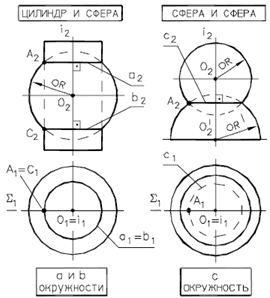
1. Сфера имеет бесчисленное множество осей вращения
2. Все оси вращения сферы проходят через ее центр
3. Если одной из двух соосных поверхностей вращения является сфера, то ее центр располагается на оси другой поверхности.
Экзаменационный билет №_20
Пересечение двух кривых поверхностей.(2-я позиционная задача)
1. Выполнить комплексный чертеж каких-либо двух пересекающихся кривых поверхностей второго порядка;
2. Определить линию их пересечения и видимость;
3. Ответить на следующие вопросы:
а) какая линия получилась в результате пересечения, ее порядок;
б) по какой схеме определялись точки линии пересечения;
в) какой принцип положен в основу выбора вспомогательных
плоскостей;
г)какие точки линии являются опорными и как они определялись
При пересечении двух плоскостей, также как и при пересечении прямой и плоскости, возможны следующие случаи:
1. Обе плоскости проецирующие.
2. Одна плоскость проецирующая, другая общего положения.
3. Обе плоскости общего положения.
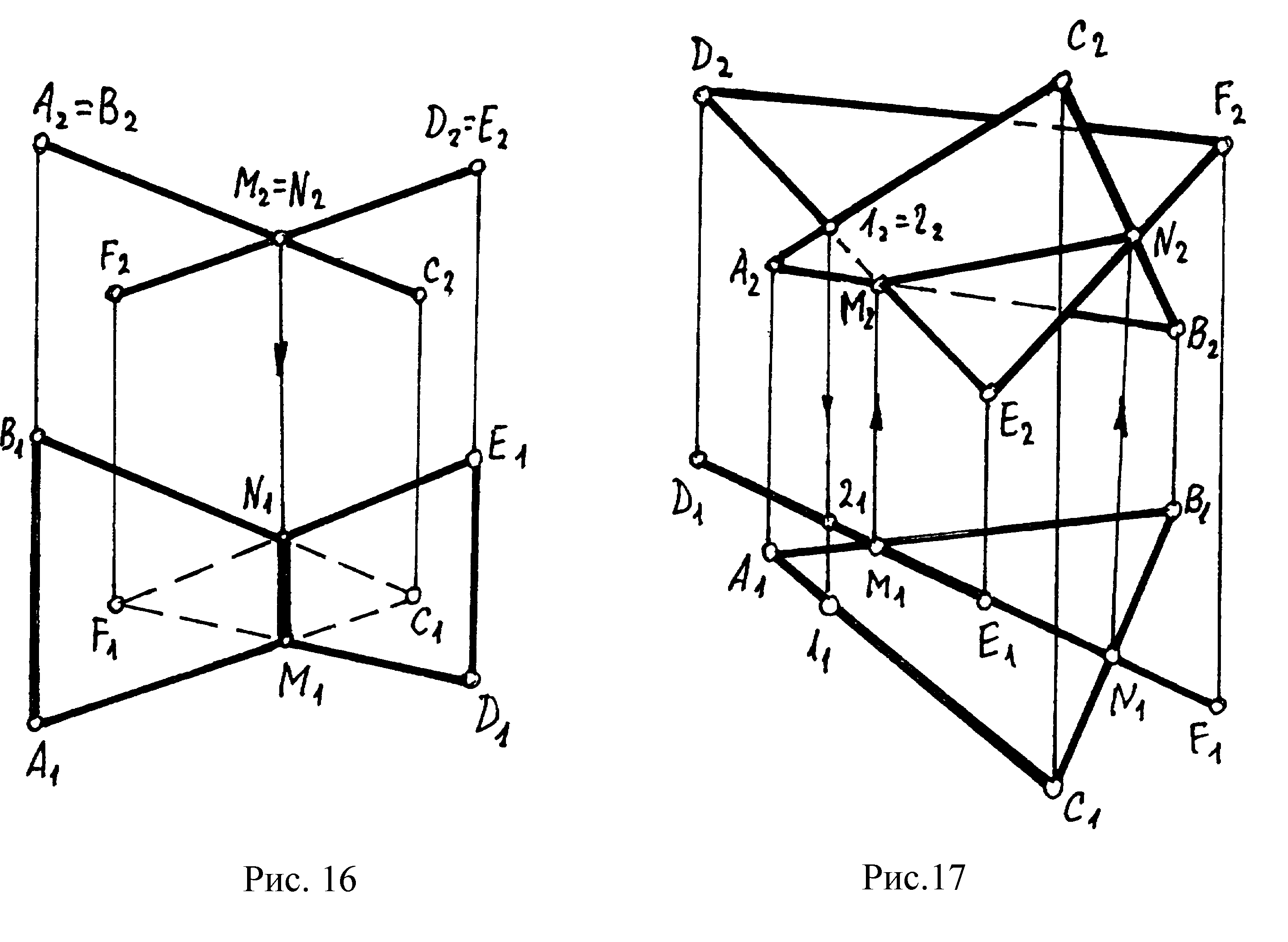
Случай 1:При пересечении плоскостей получается прямая линия. Проекции этой прямой совпадают с проекциями проецирующих плоскостей на основании их собирательных свойств. Проекции такой прямой уже имеются на комплексном чертеже и, следовательно, на требуется никаких дополнительных построений (рис.16).
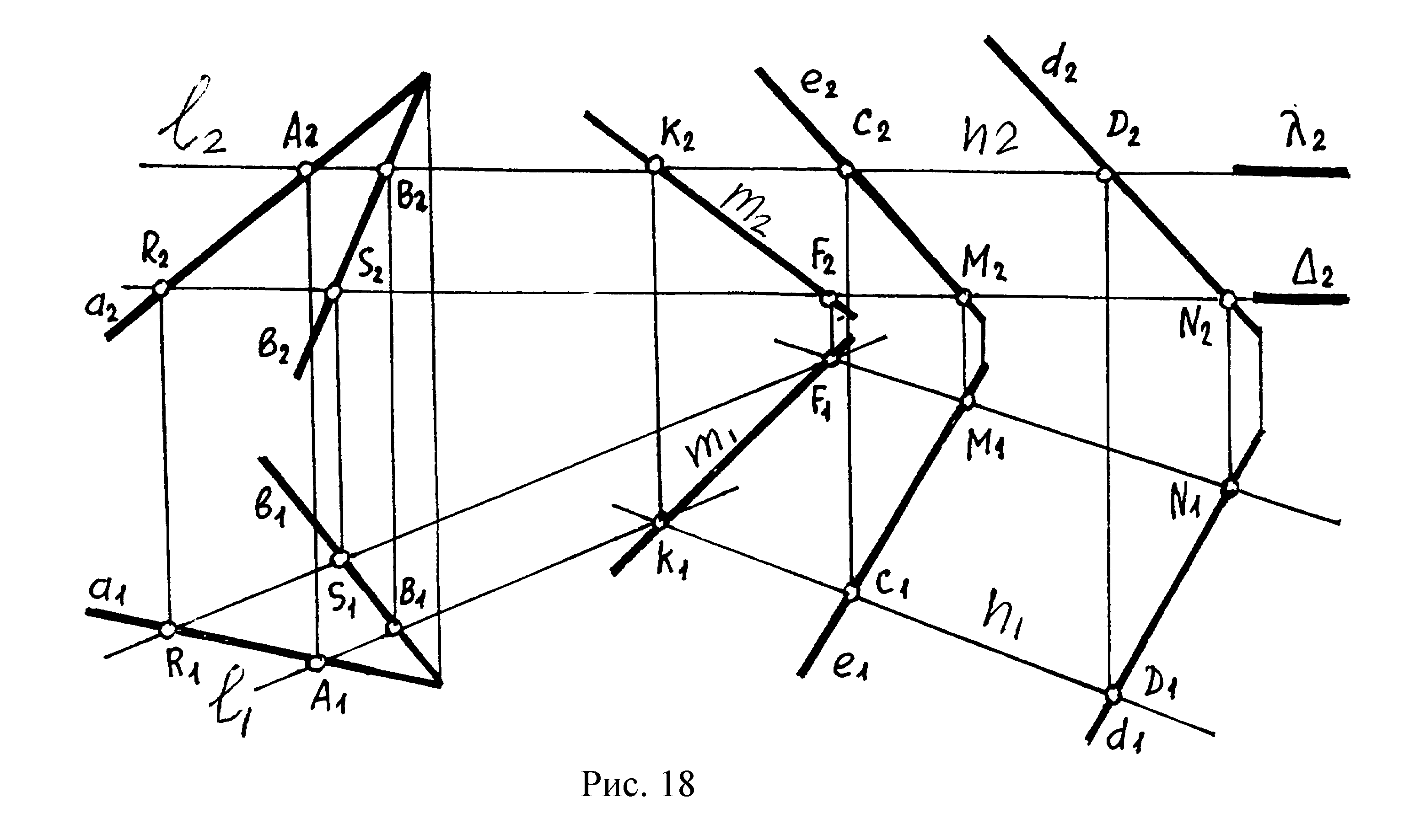
Схема решения позиционной задачи №2(случай 3):
1. 2).l(lПересечем данные плоскости Р и Q вспомогательной горизонтальной плоскостью уровня
2. Р=Çlс заданными плоскостями :lПостроим линии пересечении плоскости lQ=n(C, D).Çl(А, В),
3. Найдем точку пересечения построенных прямых ln=k. Точка K принадлежит одновременно обеим заданным плоскостям и Р, и Q, следовательно, точка K принадлежит линии пересечения заданных плоскостей.Ç
4. находится вторая точка F, которая принадлежит линии пересечения.D2). При помощи плоскостиD(DВводится вторая вспомогательная горизонтальная плоскость уровня
5. Прямая m линия пересечения плоскостей P и Q проходит через точки K и F(рис.18).
Экзаменационный билет №_21
