Системы эконометрических уравнений
70 Структурная и приведенная формы модели систем одновременных уравнений
71 Рекурсивные системы одновременных уравнений
72 Виды переменных в структурной форме модели
73 Приведенная форма модели
5 Применение эконометрики.
74 Примеры макро- и микроэкономических моделей
75 Информационные технологии эконометрических исследований
68 Эконометрические пакеты: виды программ, платформы, интерфейс, способ представления данных, дополнительные возможности.
.
Контрольные вопросы (тесты) по дисциплине «Эконометрика» для студентов специальности 080801 Прикладная информатика в экономике
1. Эконометрика – это:
1) наука, которая дает количественное выражение взаимосвязей в экономике;
2) учение о системе показателей, дающих представление об экономике;
3) различного рода цифровые данные.
2. Данные, используемые для эконометрических исследований:
1) отражают только закономерности экономических процессов;
2) неизбежно заключают в себе элементы случайных отклонений;
3) являются невоспроизводимыми заново;
4) можно воспроизвести путем проведения какого-либо эксперимента.
3. Предметом объяснения в эконометрической модели являются:
1) экзогенные переменные;
2) предопределенные переменные;
3) эндогенные переменные;
4) лаговые эндогенные переменные.
4. Экзогенные переменные – это:
1) задаваемые «извне», «автономно», в определенной степени управляемые;
2) переменные, значения которых формируются в процессе и внутри функционирования анализируемой социально-экономической системы;
3) таких переменных не существует.
5. Системы одновременных уравнений относится:
1) к классу моделей временных рядов;
2) к классу регрессионных моделей с одним уравнением;
3) к классу моделей сезонности;
4) являются самостоятельным классом эконометрических моделей.
6. Источниками информации для эконометрических исследований являются:
1) данные бухгалтерского учета;
2) данные статистической отчетности и официальной статистики;
3) результаты специально организованного экономического эксперимента на уровне страны, региона или предприятия;
4) исследователь сам выдумывает данные и обрабатывает их.
7. Происходящий в 21 веке всё ускоряющийся процесс глобализации экономики приводит к тому, что:
1) не стоит вообще строить эконометрические модели и проводить исследования – все равно результаты будут неверными;
2) в модели макроэкономических показателей страны следует включать факторы мирового рынка;
3) ни к чему не приводит, не стоит учитывать этот факт при проведении исследований.
8. Модель, где среднее значение зависимой переменной рассматривается как функция нескольких независимых переменных, это:
1) множественная регрессия;
2) простая регрессия;
3) такой модели не существует.
9. Определение аналитического выражения связи (формы связи), т.е. выбор математического уравнения, выражающего зависимость между признаками – это:
1) задача корреляционного анализа;
2) задача регрессионного анализа;
3) задача корреляционно-регрессионного анализа в целом.
10. Поле корреляции представляет собой:
1) секторную диаграмму;
2) столбиковую диаграмму;
3) точечный график в прямоугольной системе координат.
11. Одна из формул для расчета коэффициента регрессии имеет вид:
1) 
2) 
3) 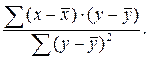
12. Коэффициент регрессии показывает:
1) на сколько процентов в среднем по совокупности изменится результат 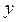 от своей средней величины при изменении фактора
от своей средней величины при изменении фактора  на 1% от своего среднего значения;
на 1% от своего среднего значения;
2) среднее изменение результата с изменением фактора на одну единицу его измерения;
3) значение результативного признака 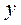 , если факторный признак
, если факторный признак  .
.
13. Коэффициент эластичности для модели парной линейной зависимости рассчитывается по формуле:
1) 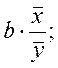
2) 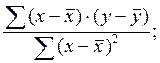
3) 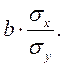
14. Остаточная сумма квадратов отклонений индивидуальных значений признака от его среднего значения имеет обозначение:
1) 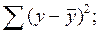
2) 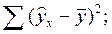
3) 
15. Статистическая значимость уравнения регрессии в целом оценивается с помощью:
1) F-критерия Фишера;
2) 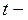 критерия Стьюдента;
критерия Стьюдента;
3) критерия Дарбина-Уотсона.
16. Для определения параметров уравнения 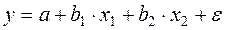 система нормальных уравнений выглядит:
система нормальных уравнений выглядит:
1) 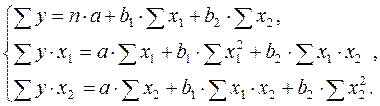
2) 
3) 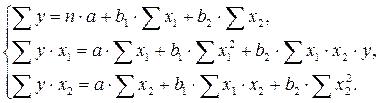
17. Частный F-критерий Фишера оценивает:
1) статистическую значимость присутствия соответствующего фактора в уравнении множественной регрессии;
2) целесообразность включения в уравнение одного фактора после другого фактора;
3) значимость коэффициентов чистой регрессии.
18. Между критерием Стьюдента и частным критерием Фишера в линейной зависимости существует следующая взаимосвязь:
1)  ;
;
2) 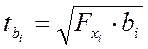 ;
;
3) 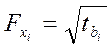 .
.
19. Функция вида  это:
это:
1) линейная функция;
2) степенная функция;
3) экспоненциальная функция.
20. Фиктивные переменные во множественной регрессии – это:
1) преобразованные в количественные качественные переменные;
2) все независимые переменные в модели;
3) таких переменных не существует.
21. Моделями временных рядов называются модели, построенные по:
1) данным, характеризующим совокупность различных объектов в определенный момент (период) времени;
2) данным, характеризующим один объект за ряд последовательных моментов (периодов) времени;
3) любым имеющимся данным об изучаемой совокупности.
22. Модель Уинтерса является моделью адаптивного прогнозирования временного ряда:
1) с аддитивной сезонностью и линейным ростом;
2) с мультипликативной сезонностью и линейным ростом;
3) моделью степенного сглаживания временного ряда.
23. Взаимопогашаемость сезонных воздействий в мультипликативной модели с сезонной компонентой выражается в том, что сумма значений сезонной компоненты по всем периодам в цикле должна быть равна:
1) 0;
2) числу периодов в цикле;
3) 4.
24. Имеются данные:
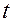 | ||||||||||||
Уровни ряда, 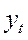 |
Этот ряд содержит сезонные колебания периодичностью:
1) 2;
2) 3;
3) 4.
25. Система уравнений, в которой каждая зависимая переменная 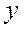 рассматривается как функция одного и того же набора факторов
рассматривается как функция одного и того же набора факторов  , называется:
, называется:
1) система рекурсивных уравнений;
2) система независимых уравнений;
3) система взаимозависимых уравнений;
4) система одновременных уравнений.
26. Связи, отображаемые графом связей, описывает:
1) приведенная форма системы уравнений;
2) структурная форма системы уравнений;
3) система независимых уравнений.
27. Если в системе эконометрических уравнений для какого-либо уравнения  , то уравнение:
, то уравнение:
1) неидентифицируемое;
2) сверхидентифицируемое;
3) идентифицируемое.
28. Представленному графу связей
 |


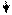


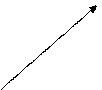


|
|

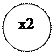
соответствует система уравнений:
 1)
1) 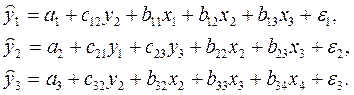
 2)
2) 
 3)
3) 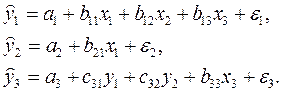
29. С позиции идентифицируемости структурные модели могут быть:
1) сверхидентифицируемые;
2) сверхъестественные;
3) суперидентифицируемые.
30. При проверке уравнений в системе на идентификацию приняты обозначения переменных:
1)  число эндогенных переменных в уравнении,
число эндогенных переменных в уравнении, 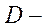 число предопределенных переменных, отсутствующих в уравнении, но присутствующих в системе;
число предопределенных переменных, отсутствующих в уравнении, но присутствующих в системе;
2)  число предопределенных переменных, отсутствующих в уравнении, но присутствующих в системе,
число предопределенных переменных, отсутствующих в уравнении, но присутствующих в системе, 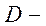 число эндогенных переменных в уравнении;
число эндогенных переменных в уравнении;
3)  число эндогенных переменных в уравнении,
число эндогенных переменных в уравнении, 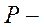 число предопределенных переменных, отсутствующих в уравнении, но присутствующих в системе.
число предопределенных переменных, отсутствующих в уравнении, но присутствующих в системе.
