Лабораторная работа №6 РЕШЕНИЕ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ МЕТОДОМ ГАУССА

Цель работы: Написать программу для решения системы линейных уравнений методом Гаусса

Теоретические основы

Метод Гаусса основан на приведении матрицы системы к треугольному виду. Этот процесс называется прямым ходом метода Гаусса. Однако к такому виду приводится лишь невырожденная матрица. В противном случае метод Гаусса неприменим.

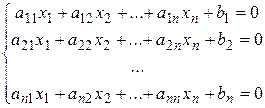
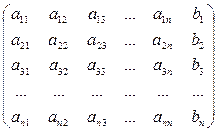
Приведение матрицы к треугольному виду описано в лабораторной работе №5.

Для исключения x₁из второго уравнения прибавим к нему первое, умноженное на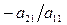

Тогда элементы модифицированной строки матрицы принимают значения:

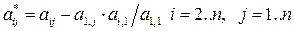
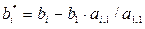
После всех преобразований матрица, описывающая систему уравнений примет вид:

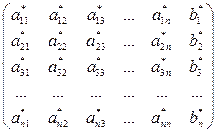
Вычисление переменных x_i производится по следующей схеме: вычислив x_n

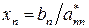
подставляем его значение в предыдущее уравнение и определяем x_n–1

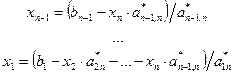
Подстановкой вновь вычисленных переменных в предыдущие уравнения находим все значения переменных.

Задание

Написать программу решения системы уравнений методом Гаусса, состоящей из n уравнений (n – задается преподавателем).

Пример для самопроверки:

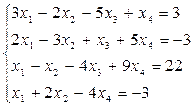
Ответ: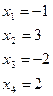

Контрольные вопросы

Лабораторная работа №7
ПРИБЛИЖЕННОЕ РЕШЕНИЕ УРАВНЕНИЯ ¦(x)=0

Цель работы: Написать программу для решения уравнений вида ¦(x)=0 итерационными методами

Теоретические основы

Задача нахождения корней нелинейных уравнений вида f(x)=0 встречается в различных областях научных исследований (здесь f(х) – некоторая непрерывная функция.) Нелинейные уравнения можно разделить на два класса – алгебраические и трансцендентные. Алгебраическими уравнениями называются уравнения, содержащие только алгебраические функции (целые, рациональные, иррациональные). В частности, многочлен является целой алгебраической функцией. Уравнения, содержащие другие функции (тригонометрические, показательные, логарифмические и др.), называются трансцендентными.

Методы решения нелинейных уравнений делятся на прямые и итерационные. Прямые методы позволяют записать корни в виде некоторого конечного соотношения (формулы). Из школьного курса алгебры известны такие методы для решения тригонометрических, логарифмических, показательных, а также простейших алгебраических уравнений.

Однако встречающиеся на практике уравнения не удается решить такими простыми методами. Для их решения используются итерационные методы, т. е. методы последовательных приближений. Алгоритм нахождения корня уравнения с помощью итерационного метода состоит из двух этапов: а) отыскания приближенного значения корня или содержащего его отрезка; б) уточнения приближенного значения до некоторой заданной степени точности.

Приближенное значение корня (начальное приближение) может быть найдено различными способами: из физических соображений, из решения аналогичной задачи при других исходных данных, с помощью графических методов. Если такие априорные оценки исходного приближения провести не удается, то находят две близко расположенные точки а и b, в которых непрерывная функция f(x) принимает значения разных знаков, т. е. f(a)f(b)<0, В этом случае между точками а и b есть по крайней мере одна точка, в которой f(x)=0. В качестве начального приближения х₀ можно принять середину отрезка [а, b], т. е. .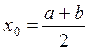

Итерационный процесс состоит в последовательном уточнении начального приближения х₀. Каждый такой шаг называется итерацией. В результате итераций находится последовательность приближенных значений корня х₁, х₂, ..., х_n. Если эти значения с ростом n приближаются к истинному значению корня, то говорят, что итерационный процесс сходится.

Ниже рассматриваются некоторые итерационные методы решения трансцендентных уравнений.

Метод деления отрезка пополам (метод бисекции)

Это один из простейших методов нахождения корней нелинейных уравнений. Он состоит в следующем. Допустим, что удалось найти отрезок [а, b], в котором расположено искомое значение корня х = с, т. е. 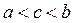. В качестве начального приближения корня с₀ принимаем середину этого отрезка, т. е. 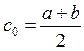. Далее исследуем значения функции f(х) на концах отрезков [а, c₀] и [c₀, b], т. е. в точках а, c₀, b. Тот из них, на концах которого f(х) принимает значения разных знаков, содержит искомый корень; поэтому его принимаем в качестве нового отрезка. Вторую половину отрезка [а, b], на которой знак f(х) не меняется, отбрасываем. В качестве первой итерации корня принимаем середину нового отрезка и т. д. Таким образом, после каждой итерации отрезок, на котором расположен корень, уменьшается вдвое, т. е. после n итераций он сокращается в 2ⁿ раз.

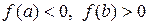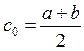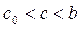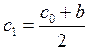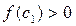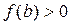Пусть для определенности (рис. 1). В качестве начального приближения корня примем . Поскольку в рассматриваемом случае f(c₀)<0, то , и рассматриваем только отрезок [c₀, b]. Следующее приближение: . При этом отрезок [c₁, b] отбрасываем, поскольку и т. е. 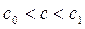. Аналогично находим другие приближения 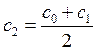и т.д.

Рисунок 1 – Метод деления отрезка пополам

Итерационный процесс продолжаем до тех пор, пока значение функции f(x) после n–й итерации не станет меньшим по модулю некоторого заданного малого числа е, т. е. 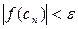. Можно также оценивать длину полученного отрезка: если она становится меньше допустимой погрешности, то счет прекращается.

Метод деления отрезка пополам довольно медленный, однако он всегда сходится, т. е. при его использовании решение получается всегда, причем с заданной точностью.

Метод простой итерации

Для использования этого метода исходное нелинейное уравнение записывается в виде:

x = f(x) (1)

Пусть известно начальное приближение корня 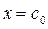. Подставляя это значение в правую часть уравнения (1), получаем новое приближение:

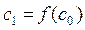
Далее, подставляя каждый раз новое значение корня в (1), получаем последовательность значений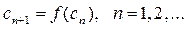

Итерационный процесс прекращается, если результаты двух последовательных итераций близки: 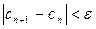. Достаточным условием сходимости метода простой итерации является условие .

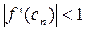Метод Ньютона

Если известно хорошее начальное приближение решения уравнения f(x)=0, то эффективным методом повышения точности является метод Ньютона (метод касательных). Метод состоит в построении итерационной последовательности 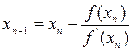, сходящейся к корню уравнения f(x)=0.

Сформулируем достаточные условия сходимости метода.

Пусть f(x)=0 определена и дважды дифференцируема на [a,b], причем 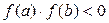, а производные 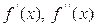сохраняют знак на этом отрезке. Тогда, исходя из начального приближения 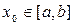, удовлетворяющего неравенству 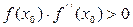,можно построить последовательность 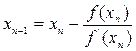, сходящуюся к единственному решению уравнения f(x)=0.

Метод Ньютона эффективен, если известно хорошее начальное приближение для корня, и в окрестности корня график функции имеет большую крутизну. В этом случае процесс быстро сходится. Если же численное значение первой производной вблизи корня мало, то процесс вычисления корня может быть очень долгим.

Задание

Написать программу для решения уравнений вида ¦(x)=0 итерационными методами

Контрольные вопросы