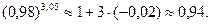Частные производные. Дифференциалы

Если приращение функции 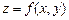получено за счет приращения независимой переменной х при неизменном значении другой независимой переменной у, то приращение функции 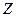называется частным приращением функции 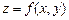по переменной 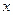и обозначается: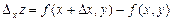

Аналогично вводится понятие частного приращения функции по переменной у: .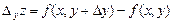

Полным называется приращение функции, получаемое за счет приращения обеих независимых переменных х, у и обозначаемое

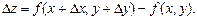
Частной производной по х от функции 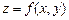называется предел отношения 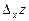к приращению 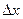при стремлении 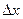к нулю.

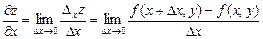
обозначаемый одним из символов: .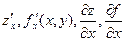

Аналогично определяется частная производная по у:

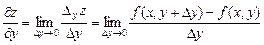
обозначаемый .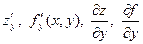

Частная производная по х вычисляется в предложении, что у – постоянная; частная производная по у вычисляется в предложении, что х – постоянная. Правила вычисления частных производных совпадают с правилами дифференцирования функции одного переменного.

Пример 10.1. Найти частные производные функции .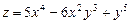

Решение. Полагая у постоянной, находим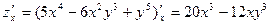

(производная по х от у⁵ равна нулю, как производная от постоянной).

При отыскании 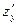переменная х рассматривается как величина постоянная, а потому

.

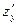
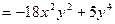Пример 10.2. Найти частные производные функции 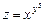. Полагая при определении 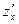величину у постоянной, получим, что z – есть степенная функция: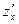

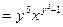
При нахождении 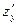, полагая х постоянной, получим, что z является показательной .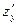

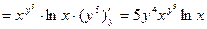Пример 10.3. Показать, что функция 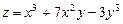удовлетворяет уравнению .

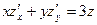Найдем частные производные ;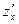

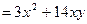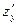
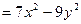
Затем первую из них умножим на х, вторую – на у и результаты сложим:

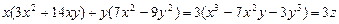
что и требовалось доказать.

Пример 10.4. Вычислить частные производные функции

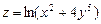в точке . .

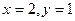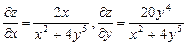Полагая 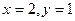, вычисляем значение производных в указанной точке

.

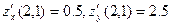Частные производные функции любого числа переменных определяются аналогично. Так, если 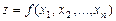, то

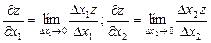и так далее.

Пример 10.5. Для функции 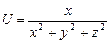частные производные имеют вид: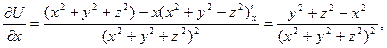

; .

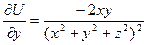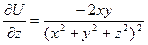Частные производные высших порядков.

Если задана функция 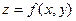, то ее частные производные 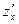и 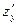также являются функциями независимых переменных х и у и от каждой из них можно вычислить производные по х и у.

Частной производной второго порядка функции 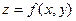называется частная производная от частной производной первого порядка.

Каждую из частных производных первого порядка можно продифференцировать по каждой из двух независимых переменных и функция двух переменных имеет четыре частные производные второго порядка. Они обозначаются:

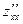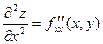= , f дифференцируется последовательно два раза по х;

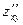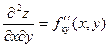= , f дифференцируется по у, а потом результат дифференцируется по х;

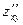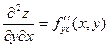= , f дифференцируется сначала по х, а потом результат дифференцируется по у;

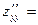
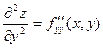, f дифференцируется последовательно два раза по у.

Производные второго порядка можно снова дифференцировать как по х, так и по у. Получим частные производные более высокого порядка.

Частная производная высшего порядка, взятая по различным переменным, называется смешанной частной производной.

.

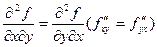Если функция 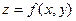и ее частные производные 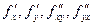определены и непрерывны в точке М (х, у) и ее окрестности, то

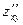
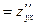
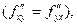
т.е. результат дифференцирования функции нескольких переменных не зависят от порядка дифференцирования.

Пример 10.6. Найти частные производные второго порядка функции

.

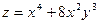Сначала находим частные производные первого порядка

.

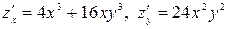Затем искомые частные производные

.

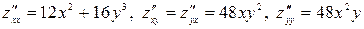Пример 10.7. 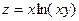. Показать, что .

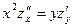Найдем: ,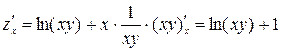

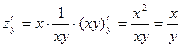и .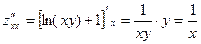

Левая и правая части данного равенства равны

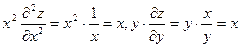и данное равенство справедливо.

Дифференциал функции двух переменных и его приложение для приближенных вычислений.

Полным дифференциалом функции 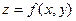называется главная часть ее полного приращения линейная относительно приращений 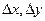(или, что то же, дифференциалов 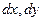). Полный дифференциал функции 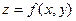обозначается символом 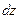и вычисляется по формуле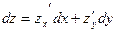

При достаточно малых приращениях аргументов полное приращение функции можно с малой относительной погрешностью заменять ее полным дифференциалом, т.е.

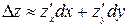, откуда .

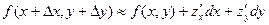Это приближенное равенство тем точнее, чем меньше величины .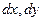

Пример 10.8. Вычислить приближенно .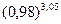

Рассмотрим функцию вида 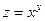. В точке (1;3) .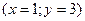

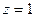Положим 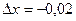и 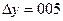(попадаем в точку 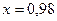и 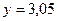). Тогда

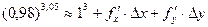
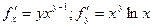
и в точке (1;3) 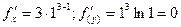и