Графический метод расчета цепей постоянного тока, содержащих нелинейные элементоы

ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА С НЕЛИНЕЙНЫМИ ЭЛЕМЕНТАМИ

Если зависимость между напряжением, приложенным к элементу, и протекающим через него током выражается линейным уравнением I=U/R или I=Ug, то такой элемент называют линейным. Предполагается, что сопротивление R и проводимость g такого элемента не зависят от величины протекающего через них тока. Вольтамперные характеристики (ВАХ) линейных элементов изображаются прямыми линиями, тангенс угла наклона которых к оси тока (рис. 3.1) определяет электрическое сопротивление элемента:

,

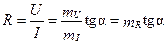где т_U, m_I и m_R — масштабы напряжения, тока и сопротивления.

Строго говоря, все элементы электрических цепей постоянного тока являются нелинейными, так как с изменением величины тока меняется температура элемента, а, следовательно, и его сопротивление. Однако в большинстве случаев нелинейность столь незначительна, что ею можно пренебречь, что позволяет значительно упростить расчеты.

Существует целый ряд элементов с ярко выраженной нелинейной зависимостью между напряжением и током. Эти элементы имеют криволинейные характеристики и поэтому называются нелинейными элементами. Они широко используются в различных областях техники и лежат в основе действия таких устройств, как выпрямители переменного тока, стабилизаторы постоянного напряжения, амплитудные ограничители и т. п.

Наиболее распространенными являются нелинейные элементы с симметричными (кривая 1) и несимметричными (кривая 2) характеристиками относительно осей координат (рис. 3.2). Сопротивления нелинейных элементов с симметричной характеристикой не зависят от направления тока, поэтому они используются в цепях как постоянного, так и переменного тока (например, термисторы, лампы накаливания, варисторы и т. д.).

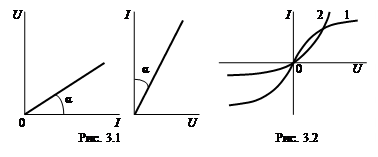
ГРАФИЧЕСКИЙ МЕТОД РАСЧЕТА ЦЕПЕЙ ПОСТОЯННОГО ТОКА, СОДЕРЖАЩИХ НЕЛИНЕЙНЫЕ ЭЛЕМЕНТОЫ

При расчете нелинейных цепей постоянного тока обычно считают известными ВАХ входящих в них нелинейных элементов. В этом случае расчет цепи наиболее просто производить графическим методом. Рассмотрим примеры такого расчета.

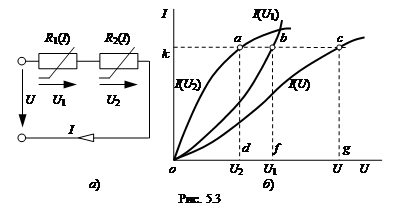
На рис. 3.3, а приведена схема нелинейной цепи, состоящей из двух последовательно соединенных нелинейных элементов R₁(I)и R₂(I)с заданными на рис. 3.3,б ВАХ I(U₁)и I(U₂).

Построим ВАХ I(U), выражающую зависимость тока I в цепи от подведенного к ней напряжения U.

Так как ток обоих участков цепи одинаков, а подведенное напряжение U=U₁+U₂, для построения характеристики I(U) достаточно просуммировать абсциссы заданных кривых I(U₁)и I(U₂)при определенных значениях тока (см. рис. 3.3, б).

Пользуясь характеристиками рис. 3.3, б, можно решить различные для данной цепи задачи. Пусть, например, задан ток I и требуется найти соответствующее ему напряжение U всей схемы и напряжения U₁, U₂отдельных ее элементов. На оси ординат графика рис. 3.3, б находим точку k,соответствующую заданному току, и проводим от нее горизонталь, пересекающую кривые I(U₁), I(U₂)и I(U). Из точек пересечения а, b и с опускаем перпендикуляры на ось абсцисс; точки пересечения их с осью абсцисс определяют искомые напряжения U₁, I(U₂)и U.

Если задано напряжение U, например, отрезком og, то по графику I(U)непосредственно можно найти ток в цепи I=m_Igc, а затем напряжения U₁и U₂, как было показано выше.

Аналогичный прием можно использовать, когда последовательно соединены не два, а большее число нелинейных элементов или когда некоторые из последовательно соединенных элементов имеют линейные характеристики. Однако в том случае, когда заданное напряжение U,подведенное к цепи, состоящей из двух последовательно соединенных нелинейных элементов, остается неизменным и требуется найти напряжения U₁и U₂ на каждом из элементов, построение общей характеристики I(U) цепи не обязательно.

Можно применить другой метод решения задачи с построением так называемой опрокинутой характеристики одного из элементов цепи. Для этого рассмотрим зависимость изменения тока I цепи, во-первых, от напряжения U₂и, во-вторых, от разности напряжений U-U₁. В первом случае эта зависимость определяется собственной характеристикой (см. рис. 3.3, б) одного элемента I(U₂), во втором случае при построении характеристики I(U-U₁)для каждого значения тока I необходимо из постоянной абсциссы U вычесть абсциссу характеристики I(U₁)первого элемента. Это равносильно построению опрокинутой характеристики элемента I(U₁)_onp от точки o', соответствующей напряжению U на рис. 3.4.

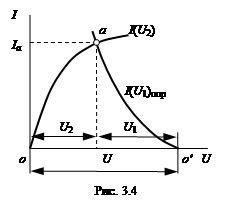
Рабочий режим второго элемента должен удовлетворять обеим характеристикам, т. е. он должен определяться точкой a пересечения этих характеристик. Перпендикуляры, опущенные на оси координат из точки пересечения, определяют значения напряжений U₁и U₂ отдельных элементов и общий ток I_a.

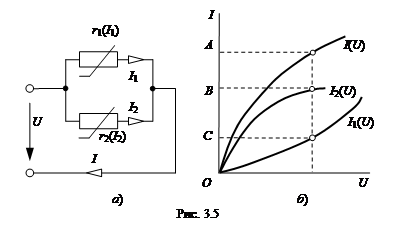
При параллельном соединении двух нелинейных элементов (рис. 3.5, а) с заданными I(U₁) и I(U₂)(рис. 3.5, б) напряжение U является общим, а ток I в неразветвленной части цепи равен сумме токов ветвей: I=I₁+I₂. Поэтому для получения общей характеристики I(U) достаточно при произвольных значениях напряжения U на рис. 3.5, б просуммировать ординаты характеристик отдельных элементов. Пользуясь этими характеристиками, как и в предыдущем случае, по заданному напряжению U можно найти токи I, I₁ и I₂. или решить обратные задачи.