Тема 3.2 Аппроксимация экспериментальных данных.

Аппроксимацией называется процесс подбора эмпирической формулы j(х) для установления из опыта функциональной зависимости y=f(x). Эмпирические формулы служат для аналитического представления опытных данных. Обычно задача аппроксимации разделяется на две части. Сначала устанавливают вид зависимости y=f(x), т.е. решают, является ли она линейной, квадратической, логарифмической и т.п. Обычно определение параметров при известном виде зависимости осуществляется по методу наименьших квадратов. При этом функция j(х) считается наилучшим приближением к f(x), если для нее сумма квадратов отклонений теоретических значений j(х) найденных по эмпирической формуле, от соответствующих опытных значений минимальна, т.е.

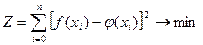
В Excel аппроксимация экспериментальных данных осуществляется путем построения их графика с последующим подбором подходящей аппроксимирующей функции (линии тренда). Возможны следующие варианты функций:

1. Линейная: y=ax+b. Обычно применяется в простейших случаях, когда экспериментальные данные убывают или возрастают с постоянной скоростью.

2. Полиномиальная: y=а₀+ a₁ x + a₂ x² +… a_n xⁿ, (п£), а_i– константы. Используется для описания экспериментальных данных, попеременно возрастающих и убывающих. Степень полинома определяется количеством экстремумов кривой. Так, например, полином второй степени может описать только один максимум или минимум, полином третьей степени – не более двух экстремумов.

3. Логарифмическая: 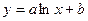, где а и b константы, ln – функция натурального логарифма. Функция применяется для описания экспериментальных данных, которые вначале быстро растут или убывают, а затем стабилизируются.

4. Степенная: y = bx^a, где а и b – константы. Аппроксимация степенной функции используется для экспериментальных данных с постоянно увеличивающейся (убывающей) скоростью роста. Данные не должны иметь нулевых или отрицательных значений.

5. Экспоненциальная: y = bе^aх, где а и b константы, е – основание натурального логарифма. Применятся для описания экспериментальных данных, которые быстро растут или убывают, а затем постепенно стабилизируется. Часто ее использование вытекает из теоретических соображений.

Степень близости аппроксимации экспериментальных данных выбранной функции оценивается коэффициентом детерминации (R²). Чем больше коэффициент детерминации (стремится к единице), тем лучше.

Для осуществления аппроксимации на диаграмме экспериментальных данных необходимо щелчком правой кнопки мыши вызвать контекстное меню и выбрать пункт Добавить линию тренда. В появившемся диалоговом окне Линия тренда, на вкладке Тип выбрать вид аппроксимирующей функции, на вкладке Параметры задаются дополнительные параметры, влияющие на отображение аппроксимирующей кривой, в частности можно установить флажки в поля Показывать уравнения на диаграмме и Поместить на диаграмму величину достоверности аппроксимации. Можно сделать прогноз о том, как будет вести себя исследуемая функция, для этого надо на вкладке Параметры указать количество периодов (от 0,5) для которых будет сделан прогноз.

Пример:Исследовать характер изменения с течением времени уровня производства некоторой продукции, и подобрать аппроксимирующую функцию, располагая следующими данными.

Год
Производство продукции	17,1	18,0	18,9	19,7	19,7

Решение:

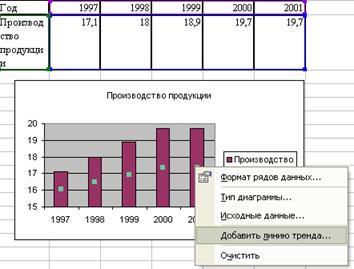
1. Введите данные и постройте гистограмму зависимости производства продукции от года.
2. Осуществите аппроксимацию полученной кривой. Для этого указатель мыши устанавливаем на одну из точек гистограммы и при помощи контекстного меню выбираем пункт Добавить линию тренда.
3. В окне Линия тренда выберите тип линии тренда логарифмическая, на вкладке Параметры установить флажки в поля Показывать уравнения на диаграмме и Поместить на диаграмму величину достоверности аппроксимации.
4. Постройте по исходным данным еще одну гистограмму и произведите те же действия, выбрав тип линии тренда Полиномиальный, степень 2, параметры те же.
5. Сравните полученные уравнения линий тренда и выберите ту, которая лучше аппроксимирует исходные данные, объясните свое решение.

Самостоятельное задание.

1. В средней школе было решено сравнить среднее число книг, прочитанных среднестатистическим восьмиклассником за год, с количеством правонарушений, совершенных подростками в микрорайоне в течение года. Проанализировали данные за 10 лет, получили следующую таблицу:

X
Y

X – среднее число книг, прочитанных за год , Y – количество правонарушений. Постройте функцию, которая наилучшим образом отображает зависимость количества правонарушений от числа книг, прочитанных за год, и запишите ее уравнение.

1. Количество вложенных в производство средств и полученная в результате прибыль соотносятся следующим образом

Кол-во средств (х)	1,6	2,0	2,5	3,0	4,0	7,0
Прибыль (y)	8,5	9,0	11,0	13,0	22,0	70,0

Запишите аналитическую зависимость между x и y. Проанализируйте полученный ответ. Какова будет прибыль предприятия, если вложить 10,0 единиц средств?