По выполнению контрольной работы №1 3 страница
Решение. 1. Областью определения функции служит множество всех действительных чисел, т.е. 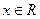 .
.
2. Функция имеет производную всюду, поэтому критические точки определяем из условия 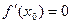 :
:
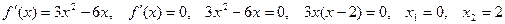 .
.
3. Находим вторую производную функции 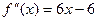 . Исследуем знак второй производной в каждой критической точке:
. Исследуем знак второй производной в каждой критической точке: 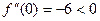 ; значит,
; значит, 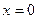 – точка максимума,
– точка максимума, 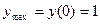 ;
;
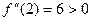 ; значит,
; значит, 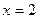 – точка минимума,
– точка минимума, 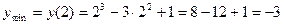 .
.
Наибольшее и наименьшее значения функции. Наибольшим значением функции называется самое большое, а наименьшим значением – самое меньшее из всех ее значений.
Функция может иметь только одно наибольшее значение и только одно наименьшее значение или может не иметь их совсем.
Нахождение наибольшего и наименьшего значений непрерывных функций основывается на следующих свойствах этих функций:
1) если в некотором открытом промежутке 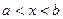 (конечном или бесконечном) функция
(конечном или бесконечном) функция 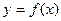 непрерывна и имеет только один экстремум и если это максимум, то он является наибольшим значением функции, а если минимум – наименьшим значением функции в этом промежутке;
непрерывна и имеет только один экстремум и если это максимум, то он является наибольшим значением функции, а если минимум – наименьшим значением функции в этом промежутке;
2) если функция 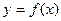 непрерывна на отрезке
непрерывна на отрезке 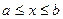 , то она обязательно имеет на этом отрезке наибольшее и наименьшее значения. Эти значения достигаются ею или в точках экстремума, лежащих внутри отрезка, или на концах этого отрезка.
, то она обязательно имеет на этом отрезке наибольшее и наименьшее значения. Эти значения достигаются ею или в точках экстремума, лежащих внутри отрезка, или на концах этого отрезка.
Поэтому, что бы найти наибольшее и наименьшее значения функции на отрезке 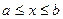 , где она непрерывна, следует:
, где она непрерывна, следует:
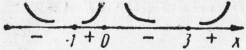 Рис. 9. Рис. 9. | 1. Найти экстремумы функции на данном отрезке. 2. Найти значения функции на концах отрезка: 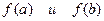 . 3. Из всех найденных значений выбрать наибольшее и наименьшее. . 3. Из всех найденных значений выбрать наибольшее и наименьшее. |
Пример 18. найти наибольшее и наименьшее значение функции 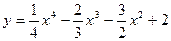 на отрезке
на отрезке 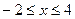 .
.
Решение. 1. Найдем экстремумы функции, для чего найдем производную функции и критические точки I рода из условия 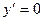 :
:
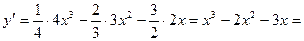
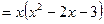 ;
; 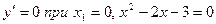 ,
, 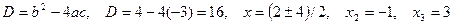 .
.
Отметим критические точки I рода 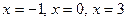 на числовой прямой (рис. 9).
на числовой прямой (рис. 9).
Исследуем знак производной в каждом из полученных интервалов: 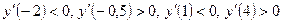 .
.
Таким образом,
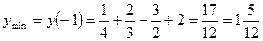 ;
;
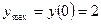 ;
;
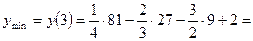
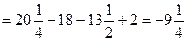 .
.
2. Найдем значения функции на концах отрезка:
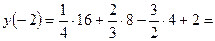
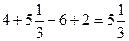 ;
; 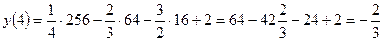 .
.
3. Итак, наибольшее значение функции 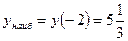 , а наименьшее значение функции
, а наименьшее значение функции 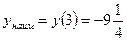 .
.
Пример 19. Требуется изготовить закрытый цилиндрический бак объемом 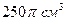 . Какими должны быть его размеры, что бы на его изготовление пошло наименьшее количество материала?
. Какими должны быть его размеры, что бы на его изготовление пошло наименьшее количество материала?
Решение. Здесь требуется определить радиус основания R и высоту Н цилиндра, что бы при заданном объеме площадь его полной поверхности была наименьшей.
Площадь полной поверхности цилиндра вычисляется по формуле:
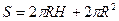 .
.
Наименьшее значение этой функции и следует определить. Так как S является функцией двух независимых переменных, то одну из них надо исключить. Известно, что объем цилиндра 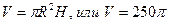 . Выразим Н через V:
. Выразим Н через V:
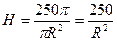 .
.
Тогда
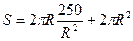 ,
, 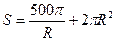 .
.
1. Областью определения функции S являются положительные значения радиуса, т.е. 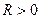 .
.
2. Находим производную:
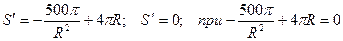 ,
,
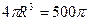 ,
, 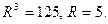
3. Находим вторую производную:
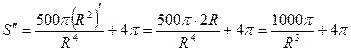 .
.
Так как 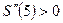 , то при
, то при 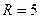 имеет место минимум функции S, который и является наименьшим значением функции S. Тогда
имеет место минимум функции S, который и является наименьшим значением функции S. Тогда 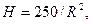 или
или 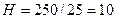 .
.
Итак, на изготовление цилиндрического бака пойдет наименьшее количество материала, если длина радиуса основания цилиндра равна 5см, а высота цилиндра 10см.
Пример 20. Требуется изготовить ящик с крышкой, стороны основания которого относятся как 1:2, а площадь поверхности 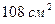 . Какими должны быть его размеры, что бы его объем был наибольшим?
. Какими должны быть его размеры, что бы его объем был наибольшим?
Решение. Здесь требуется определить стороны основания a и b и высоту Н прямоугольного параллелепипеда, что бы заданной площади полной поверхности его объем был наибольшим.
Из условия, 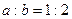 , откуда
, откуда 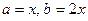 . Объем прямоугольного параллелепипеда равен
. Объем прямоугольного параллелепипеда равен 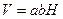 или
или 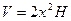 . Надо исключить переменную Н. Известно, что
. Надо исключить переменную Н. Известно, что 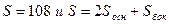
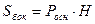 . Имеем:
. Имеем:
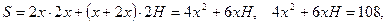
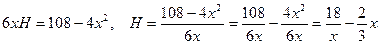 .
.
Тогда
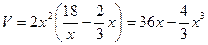 .
.
Наибольшее значение этой функции и следует определить.
1. Областью определения функции V являются положительные значения х, т.е. 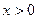 .
.
2. Находим производную:
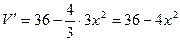 ;
; 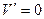 при
при 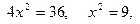
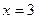 .
.
3. Находим вторую производную: 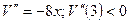 , т.е.
, т.е. 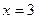 функция имеет максимум, который и служит наибольшим значением функции. При этом:
функция имеет максимум, который и служит наибольшим значением функции. При этом:
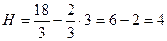 .
.
Итак, объем ящика является наибольшим, если стороны его основания имеют длину 3 и 6см, а высота 4см.
Пример 21. Число 10 разбить на два положительных слагаемых так, что бы сумма их кубов была наименьшей.
Решение. Пусть одно из слагаемых равно  , тогда другое слагаемое есть
, тогда другое слагаемое есть 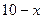 . Сумма кубов этих слагаемых равна
. Сумма кубов этих слагаемых равна
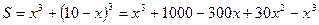 ,
, 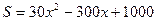 .
.
Наименьшее значение этой функции и надо определить.
1. Областью определения функции 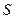 являются положительные значения
являются положительные значения  , т.е.
, т.е. 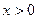 .
.
2. Находим производную:
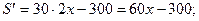
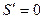 при
при 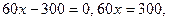
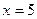 .
.
3. Находим вторую производную: 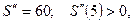 т.е. при
т.е. при 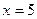 функция
функция 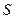 имеет минимум, который и является наименьшим значением функции.
имеет минимум, который и является наименьшим значением функции.
Итак, число 10 надо разложить на два равных слагаемых: 5 и 5.
Пример 22. Закон прямолинейного движения тела задан уравнением 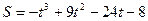 (
( 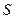 – в метрах,
– в метрах, 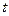 – в секундах). Найти максимальную скорость движения тела.
– в секундах). Найти максимальную скорость движения тела.
Решение. Скорость движения тела в данный момент времени равна производной пути 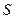 по времени
по времени 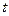 :
:
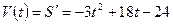 .
.
Исследуем эту функцию на экстремум с помощью второй производной: 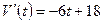 ,
, 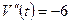 . Вторая производная отрицательна; следовательно, скорость является наибольшей при
. Вторая производная отрицательна; следовательно, скорость является наибольшей при 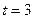 .
.
Максимальная скорость движения составляет:
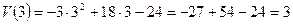 ,
, 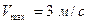 .
.
Направление вогнутости и точки перегиба кривой. Говорят, что на промежутке 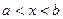 кривая обращена выпуклостью вверх или выпукла
кривая обращена выпуклостью вверх или выпукла 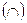 , если она лежит ниже касательной, проведенной в любой ее точке (рис. 10).
, если она лежит ниже касательной, проведенной в любой ее точке (рис. 10).
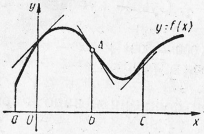 Рис 10. Рис 10. | Говорят, что на промежутке 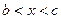 кривая обращена выпуклостью вниз или вогнута кривая обращена выпуклостью вниз или вогнута 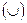 , если она лежит выше касательной, проведенной в любой ее точке (рис 10.) Точкой перегиба непрерывной кривой называется точка А (рис 10.), при переходе через которую кривая меняет свою вогнутость на выпуклость или наоборот. , если она лежит выше касательной, проведенной в любой ее точке (рис 10.) Точкой перегиба непрерывной кривой называется точка А (рис 10.), при переходе через которую кривая меняет свою вогнутость на выпуклость или наоборот. |
Достаточное условие выпуклости (вогнутости) кривой. График дифференцируемой функции 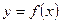 является выпуклым на промежутке
является выпуклым на промежутке 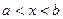 , если вторая производная функция отрицательна в каждой точке этого промежутка:
, если вторая производная функция отрицательна в каждой точке этого промежутка: 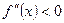 при
при 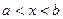 .
.
График дифференцируемой функции 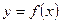 является вогнутым на промежутке
является вогнутым на промежутке 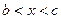 , если вторая производная функции положительна в каждой точке этого промежутка:
, если вторая производная функции положительна в каждой точке этого промежутка: 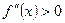 при
при 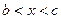 .
.
Точки, в которых вторая производная функции равна нулю, или бесконечности, или не существует, называются критическими точками II рода.
Если при переходе через критическую точку II рода  вторая производная функции меняет знак, то
вторая производная функции меняет знак, то  – абсцисса точки перегиба. Ордината точки перегиба равна значению функции в точке
– абсцисса точки перегиба. Ордината точки перегиба равна значению функции в точке 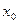 . Точка
. Точка 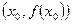 – точка перегиба графика функции
– точка перегиба графика функции 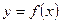 .
.
Чтобы найти направление вогнутости и точки перегиба кривой, следует:
1. Найти область определения функции.
2. Найти вторую производную функции и критические точки II рода.
3. Отметить границы области определения и критические точки II рода на числовой прямой.
4. Исследовать знак второй производной в каждом из полученных интервалов.
5. Записать промежутки выпуклости и вогнутости, абсциссу точки перегиба и вычислить ее ординату.
Пример 23. Определить направление вогнутости и точки перегиба кривой 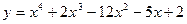
Решение. 1. Областью определения функции служит множество всех действительных чисел, т.е. 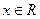 .
.
2. Найдем вторую производную функции и критические точки II рода из условия 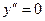 :
:
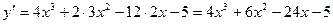 ;
;
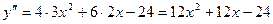 ;
;
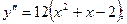
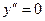 при
при 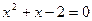 ,
,
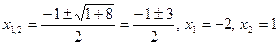 .
.
3. Отметим критические точки II рода 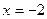 и
и 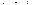 на числовой прямой (рис. 11).
на числовой прямой (рис. 11).
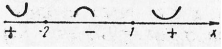 Рис. 11 Рис. 11 |  Рис 12. Рис 12. |
4.Исследуем знак второй производной в каждом из полученных интервалов: 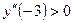 ,
, 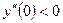 ,
, 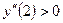 .
.
5. Кривая вогнута при 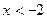 и
и 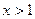 ; кривая выпукла при
; кривая выпукла при 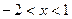 ;
;
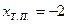 ,
, 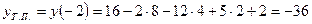 ;
;
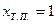 ,
, 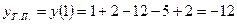 .
.
Точки перегиба 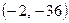 ,
, 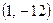 .
.
Общая схема исследования функции и построение их графиков.
1. Найти область определения функции и поведение функции в границах области определения.
2. Выяснить вопрос о четности, нечетности и периодичности функции.
3. Найти точки пересечения графика функции с осями координат.
4. Найти промежутки монотонности и экстремумы функции.
5. Найти направление вогнутости и точки перегиба графика функции.
6. Построить график функции, используя все полученные результаты исследования. Если их окажется недостаточно, то следует найти несколько точек графика функции, исходя из ее уравнения.
Построение графика функции целесообразно выполнять по его элементам, вслед за выполнением отдельных пунктов исследования.
Пример 24. Построить график функции 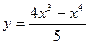 .
.
Решение. 1. Областью определения функции служит множество всех действительных чисел, т.е. 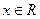 . Далее, находим
. Далее, находим 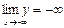 ,
, 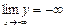 .
.
2. Выясняем вопрос о четности или нечетности функции:
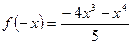 ,
, 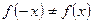 ,
, 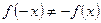 .
.
Значит, функция не является ни четной, ни нечетной.
3. Найдем точки пересечения графика функции с осями координат:
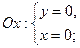
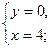
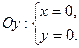
- Находим промежутки монотонности и экстремумы функции:
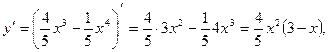
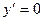 при
при 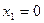 и
и 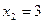 .
.
Отметим критические точки I рода 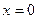 и
и 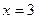 на числовой прямой (рис. 12) и исследуем знак производной в каждом из полученных интервалов:
на числовой прямой (рис. 12) и исследуем знак производной в каждом из полученных интервалов: 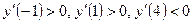 .
.
Функция возрастает при 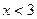 и убывает при
и убывает при 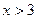 ;
; 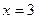 – точка максимума,
– точка максимума,
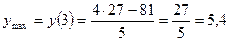 .
.
5. Находим направление вогнутости и точки перегиба графика функции:
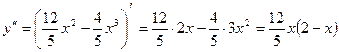 .
.
Итак, 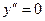 при
при 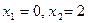 .
.
Отметим критические точки II рода 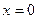 и
и 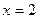 на числовой прямой (рис. 13) и исследуем знак второй производной в каждом из полученных интервалов:
на числовой прямой (рис. 13) и исследуем знак второй производной в каждом из полученных интервалов: 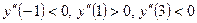 .
.
График функции является выпуклым при 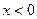 и
и 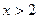 ,и вогнутым при
,и вогнутым при 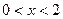 ;
;
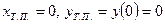 ;
;
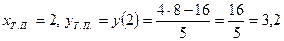 .
.
Точки перегиба графика функции 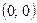 и
и 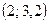 .
.
Отметим все полученные точки в системе координат и соединим их плавной кривой (рис.14).
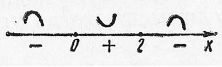 Рис 13. Рис 13. | 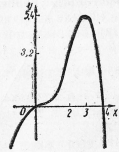 Рис. 14 Рис. 14 |
Для уточнения графика найдем дополнительную точку 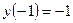 .
.
Неопределенный интеграл.
.
Дифференцируемая функция 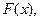 а<x<b называется первообразной для функции f(x) на интервале a<x<b, если
а<x<b называется первообразной для функции f(x) на интервале a<x<b, если 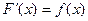 для каждого a<x<b.
для каждого a<x<b.
Так для функции 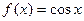 первообразной служит функция
первообразной служит функция 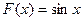 , поскольку
, поскольку 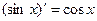 .
.
Для заданной функции ее первообразная определяется неоднозначно.
Справедлива теорема: если F(x) – первообразная для f(x) на некотором промежутке, то и функция F(x)+C, где С – любая постоянная, также является первообразной для функции f(x) на этом промежутке. Обратно: каждая функция, являющаяся первообразной для f(x) в данном промежутке, может быть записана в виде F(x)+C.
Значит, достаточной найти для данной функции f(x) только одну первообразную функции F(x), что бы знать первообразные, так как они отличаются друг от друга только на постоянную величину.
Совокупность F(x)+C всех первообразных функций f(x) на интервале a<x<b называют неопределенным интегралом от функции f(x) на этом интервале и пишут 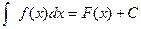 . Здесь f(x)dx – подынтегральное выражение; f(x) – подынтегральная функция; x – переменная интегрирования; С – произвольная постоянная.
. Здесь f(x)dx – подынтегральное выражение; f(x) – подынтегральная функция; x – переменная интегрирования; С – произвольная постоянная.
Например, 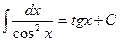 , так как
, так как 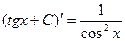 .
.
Если функция f(x) имеет на некотором промежутке хотя бы одну первообразную, то ее называют интегрируемой на этом промежутке. Можно доказать, что любая функция, непрерывная на отрезке a£x£b, интегрируема на этом отрезке.
Свойства неопределенного интеграла.
1. Производная неопределенного интеграла равна подынтегральной функции; дифференциал неопределенного интеграла равен подынтегральному выражению:
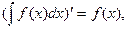
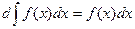 .
.
2. Неопределенный интеграл от дифференциала функции равен этой функции, сложенной с произвольной постоянной, т.е.
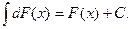
3. Постоянный множитель можно выносить за знак неопределенного интеграла:
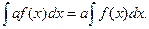
4. Неопределенный интеграл от алгебраической суммы функции равен такой же алгебраической сумме неопределенных интегралов от каждой функции:
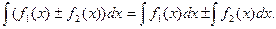
Основные формулы интегрирования (табличные интегралы).
Из каждой формулы дифференцирования вытекает соответствующая ей формула интегрирования. Например, из того, что 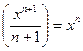 , следует равенство
, следует равенство 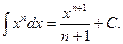
Ниже приведена таблица основных интегралов:
1. 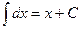 2. 2. 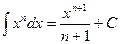 (n¹ –1) 3. (n¹ –1) 3. 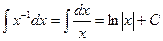 4. 4. 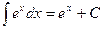 5. 5. 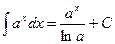 6. 6. 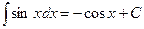 | 7. 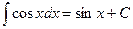 8. 8. 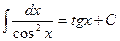 9. 9. 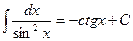 10. 10. 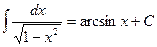 11. 11. 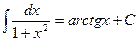 |
Справедливость этих формул можно проверить дифференцированием.
