Варіаційний ряд та його характеристики. Полігон. Гістограма
Безпосередньо із вибірки важко зробити якісь висновки про властивості досліджуваної ознаки, тому проводять первинну обробку результатів спостережень. Спочатку запишемо вибіркові значення в порядку зростання і відповідно їх пронумеруємо. Одержимо послідовність x1≤ x2≤…≤ xn) значень випадкової величини, яку називають варіаційним рядом.
Окремі значення xi варіаційного ряду називають варіантами. Якщо серед варіант є однакові, то ми знову їх перенумеруємо, приписуючи однаковим варіантам той самий номер. Нехай у варіаційному ряді варіанта хi повторюється ni разів (i = 1,k, n1 + n2 +... + nk = n). Числа пі називають частотами, а їх відношення до об'єму вибірки 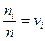 - відносними частотами. За отриманими значеннями варіант, частот і відносних частот можна побудувати таблиці
- відносними частотами. За отриманими значеннями варіант, частот і відносних частот можна побудувати таблиці
| xi | x1 | x2 | … | xk | xi | x1 | x2 | … | xk | |
| ni | n1 | n2 | … | nk | vi | v1 | v2 | … | vk |
які називають відповідно розподілами частот і відносних частот. Розподіли частот і відносних частот називають також статистичним розподілом вибірки.
Крім вибіркового середнього і вибіркової дисперсії, використовують ряд інших числових характеристик варіаційного ряду.
Означення 5. Модою М0 варіаційного ряду називають варіанту, яка має найбільшу частоту.
Наприклад, для ряду з прикладу 1 М0 = 7.
Означення 6. Медіаною Ме варіаційного ряду називають варіанту, яка ділить ряд на дві частини, рівні за кількістю варіант.
Якщо число варіант непарне, тобто k=2т+1, то Ме = хт+1. При парному k = 2т медіана 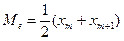 .
.
Означення 7. Варіаційним розмахом R називають різницю між крайніми (найбільшою і найменшою) варіантами: R = xmax - xmin
Означення 8. Середнім абсолютним відхиленням θ називають середнє арифметичне з абсолютних значень відхилень варіант від вибіркового середнього значення: θ 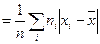 .
.
Означення 9. Коефіцієнтом варіації V1 (за середнім абсолютним відхиленням) називають визначене в процентах відношення середнього абсолютного відхилення до вибіркового середнього: 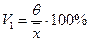
Означення 10. Коефіцієнтом варіації V2 (за середнім квадратичним відхиленням) називають визначене в процентах відношення вибіркового середнього квадратичного відхилення до вибіркового середнього: 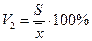
Означення 11. Полігоном частот називають ламану, відрізки якої сполучають точки (х1,п1),(х2,п2),...,(хk,пk) в прямокутній системі координат xi0ni.
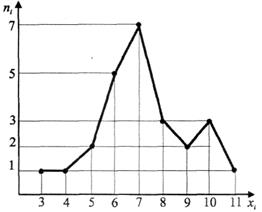 Для побудови полігона частот на осі абсцис відкладаємо варіанти xi, а на осі ординат - відповідні їм частоти. Точки (хi, ni) сполучаємо відрізками прямих.
Для побудови полігона частот на осі абсцис відкладаємо варіанти xi, а на осі ординат - відповідні їм частоти. Точки (хi, ni) сполучаємо відрізками прямих.
Приклад 1. Із прочитаних 16 слів 25 студентів правильно відтворили такі кількості слів: 8, 10, 6, 6, 7, 9, 7, 7, 3, 4, 7, 5, 7, 11, 8, 6,10, 5, 6, 8, 6, 7, 7, 9, 10.
Полігон частот для прикладу 1 показано на рисунку.
 Означення 12. Полігоном відносних частотназивають ламану, відрізки якої сполучають точки (х1,v1), (х2,v2),...,(хк,vk) в прямокутній системі координат xi0vi.
Означення 12. Полігоном відносних частотназивають ламану, відрізки якої сполучають точки (х1,v1), (х2,v2),...,(хк,vk) в прямокутній системі координат xi0vi.
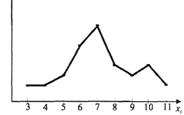
Для побудови полігона відносних частот на осі абсцис відкладають варіанти хi, а на осі ординат - відповідні їм відносні частоти vi. Точки (xi, vi) сполучають відрізками прямих. Полігон відносних частот для прикладу 1 показано на рисунку.
Означення 13. Гістограмою частот називають східчасту фігуру, яка складається з прямокутників, основами яких є часткові інтервали довжиною h, а висоти дорівнюють . Величину називають щільністю частоти.
