Давление, энтропия и статистический интеграл

Из первого начала термодинамики

,

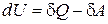и из определений энтропии и работы

,

,

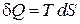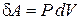находим

,

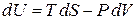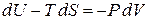. (2.32)

Подставляем в (2.31а)

,

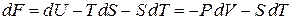сравниваем с (2.30а) при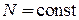

,

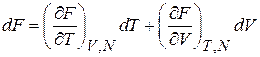получаем

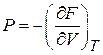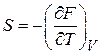, . (2.33)

Используем (2.25)

,

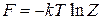получаем давление

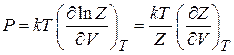, (2.34)

и энтропию

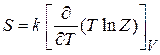. (2.35)

теоремА Бора – Ван-Левен(1919 г.)

Система зарядов, подчиняющаяся классической физике, не проявляет магнитных свойств. Теорему доказал Нильс Бор в 1911 г. и независимо мисс Хендрика Йоханна Ван Левен в 1919 г.

Нильс Бор (1885–1962)

Доказательство:

Используем гамильтониан системы N зарядов в электромагнитном поле

,

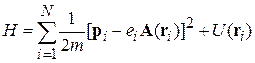где 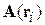– векторный потенциал магнитного поля в точке нахождения заряда 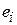; 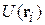– потенциальная энергия заряда 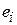. Получаем статистический интеграл системы

.

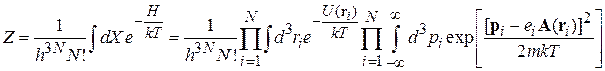Благодаря бесконечным пределам интеграла по импульсам при замене 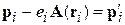статистический интеграл оказывается не зависящим от магнитного поля. Следовательно, классический газ зарядов не обладает магнитными свойствами.

Теорема не применима, если энергия взаимодействия U зависит от импульсов зарядов, а также, если учитываются квантовые свойства частиц.

ПРИМЕР 1

Идеальный газ из N атомов находится в объеме V. При температуре Т атомы совершают поступательные движения. Найти статистический интеграл, внутреннюю энергию и давление.

1. Статистический интеграл атома

Используем

,

.

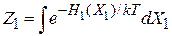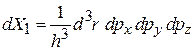Гамильтониан атома

.

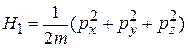Подстановка дает

.

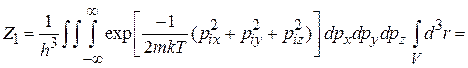
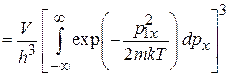Учтено, что координаты и импульсы разделены и

.

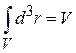Используем интеграл Пуассона

,

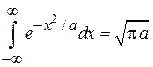для интеграла в квадратных скобках находим 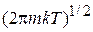. В результате статистический интеграл поступательного движения частицы

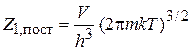. (П.3.1)

С учетом

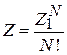
получаем статистический интеграл поступательного движения газа

.

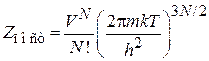2. Внутренняя энергия

Вычисляем (2.26)

.

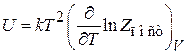Из 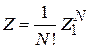находим

.

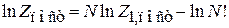По формуле Стирлинга

, ,

,

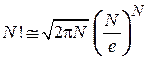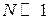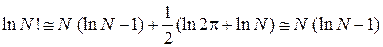тогда

.

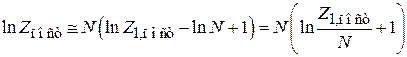С учетом (П.3.1)

,

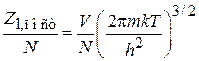получаем

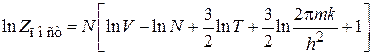. (П.3.1а)

Из (2.26)

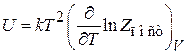
получаем

,

.

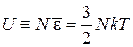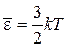Результат совпадает с выражением, найденным из микроканонического распределения, а также с известной формулой термодинамики идеального газа, что позволяет отождествить k с постоянной Больцмана.

3. Давление

Из (2.34) и (П.3.1а) находим

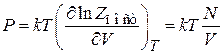
и получаем

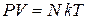– уравнение идеального газа,

, , .

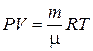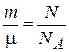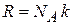ПРИМЕР 2

Атомы двухатомной молекулы при температуре Т совершают колебания с частотой ω. Найти статистический интеграл колебаний.

Молекулу считаем линейным гармоническим осциллятором. Гамильтониан

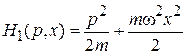
подставляем в (2.17)

, ,

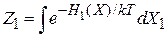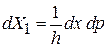находим

.

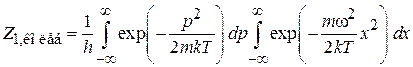Используем интеграл Пуассона

,

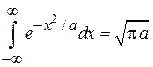для интегралов получаем соответственно

, .

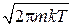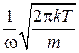В результате статистический интеграл колебательного движения молекулы

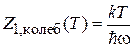. (П.3.5)

ПРИМЕР 3

Молекула массой m состоит из двух одинаковых атомов, находящихся на расстоянии 2r и вращающихся вокруг центра масс при температуре Т. Найти статистический интеграл вращений.

При вращении изменяется угловое положение атомов. Используем сферические координаты с центром в точке симметрии молекулы. На рисунке черный круг – атом, второй атом в симметричной точке не показан.

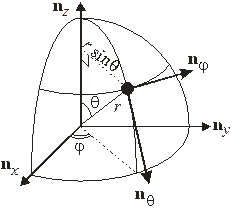
При вращении изменяются углы φ и θ. Угловые скорости связаны с линейными скоростями

вдоль 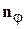скорость ,

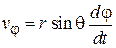вдоль 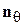скорость .

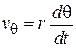Обобщенными координатами фазового пространства являются углы φ и θ. Для нахождения импульсов, соответствующих этим координатам, используем уравнение Лагранжа

,

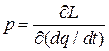где функция Лагранжа

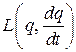
зависит от координаты и скорости.

Жозеф Луи Лагранж (1736–1865)

При отсутствии потенциальной энергии функция Лагранжа равна кинетической энергией. Для двухатомной молекулы получаем

,

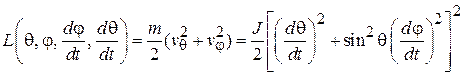где

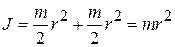
– момент инерции молекулы относительно прямой, перпендикулярной к оси молекулы и проходящей через центр масс. Обобщенные импульсы находим из уравнений

,

,

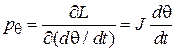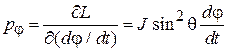тогда

, .

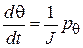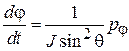Результаты подставляем в

,

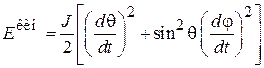и находим гамильтониан

.

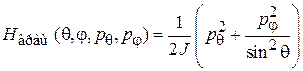Статистический интеграл частицы (2.17)

,

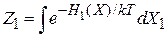где

,

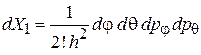получает вид

.

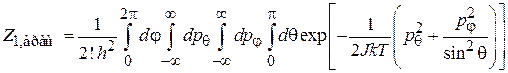Интегрируем вначале по j, затем по p_q, p_j и в конце по θ. С учетом

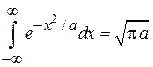
находим

,

.

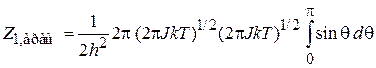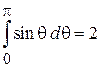Статистический интеграл вращательного движениямолекулы

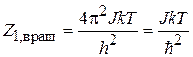. (П.3.6)