Расчет переходных процессов в нелинейной цепи постоянного тока.

4.1. Нелинейная цепь после коммутации для рассматриваемого случая изображена на рис. 21

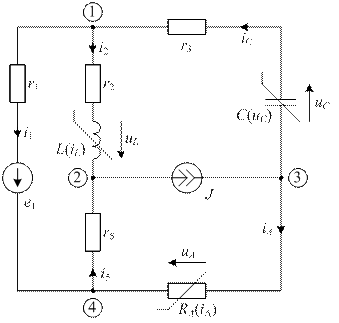рис. 21

Нелинейные характеристики элементов R_A(i_A), G_B(u_B), L(i_L), C(u_C) определяются как статические параметры ВАХ сопротивления R_A, проводимости G_B, ВАХ индуктивности, КВХ емкости.

, , ,

С учетом характеристик u_A(i_A), i_B(u_B), ψ(i_L) и q(u_C) получим

RA(iA), Ом					46,3
iA, А	0,3	0,5

L(iL), Гн	0,63	0,63	0,63	0,6	0,42	0,24	0,132	0,093	0,072	0,06
iL, А	0,05	0,1	0,2	0,3	0,5

C(uC)·10-6, Ф			33,5	20,5	15,17
uC, В

GB, 1/Ом	0,333	0,333	0,2	0,0833	0,05385	0,04
uB, В

Кубическая сплайновая аппроксимация и ее графики приведены ниже.

Вольт-амперная характеристика НЭ-А

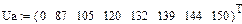
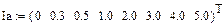
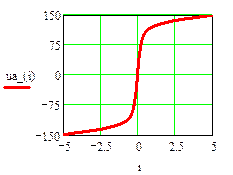
Вольт-амперная характеристика НЭ-Б

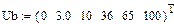
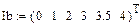
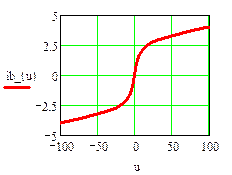
Вебер-амперная характеристика нелинейной индуктивности

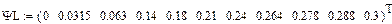
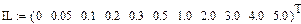
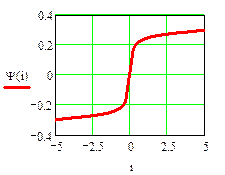
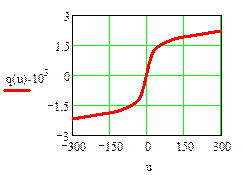
Кулон-амперная характеристика нелинейной ёмкости

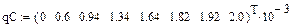
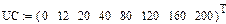
Интерполяция ВАХ НЭ с помощью кубических сплайнов

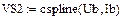
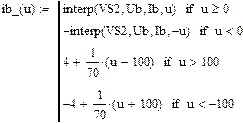
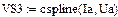
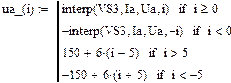
Интерполяция характеристик нелинейных реактивных элементов

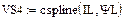
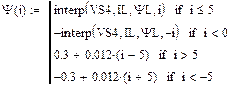
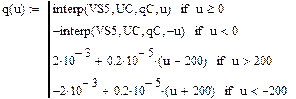
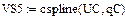
Статическая характеристика сопротивления НЭ-А

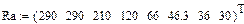
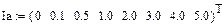
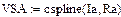
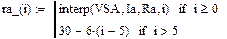
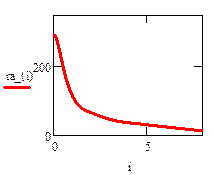
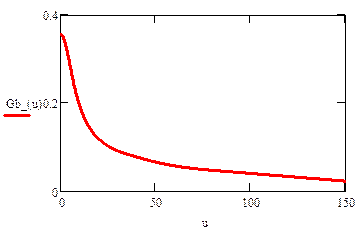
Статическая характеристика проводимости НЭ-Б

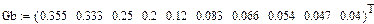
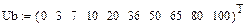
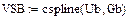
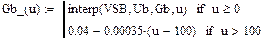
Статическая характеристика нелинейной индуктивности

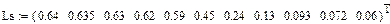
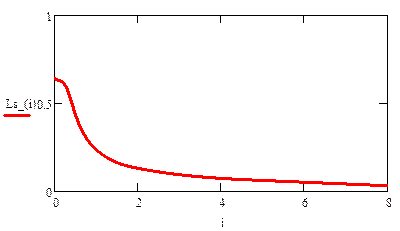
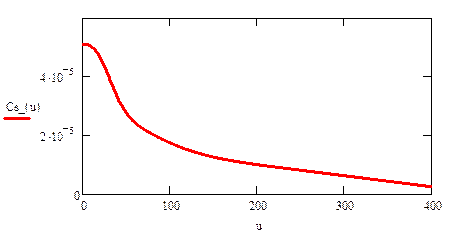
Статическая характеристика нелинейной ёмкости

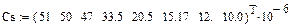
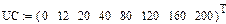
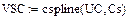
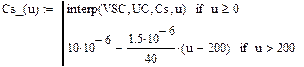
4.2. Расчет нелинейной цепи до коммутации.

Схема до коммутации приведена на рис. 22

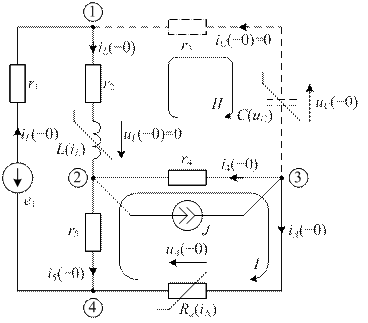рис. 22

При постоянных источниках e₁ и J в схеме до коммутации ток и . На рис. 22 ветвь с емкостью изображена пунктиром, так как ток в ней отсутствует.

4.2.1. Расчет установившегося режима графическим методом.

В схеме рис. 22 один нелинейный элемент R_A(i_A), поэтому расчет можно провести используя метод эквивалентного генератора.

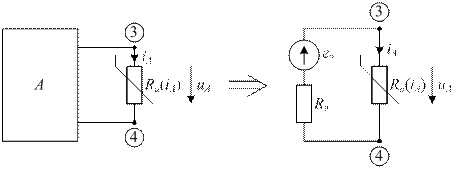рис. 23

Параметры эквивалентного генератора линейной части схемы e_э и r_э находятся расчетом цепи рис. 24.

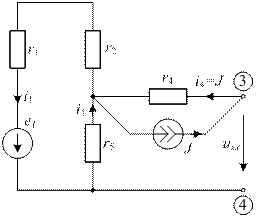рис. 24

По 2 закону Кирхгофа

Таким образом

Эквивалентное сопротивление генератора находится из пассивной схемы рис. 25

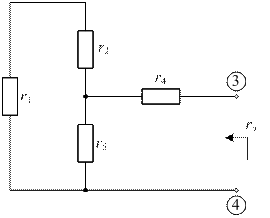рис. 25

Графический расчет схемы рис. 23 с использованием внешней характеристики источника дает (рис. 26)

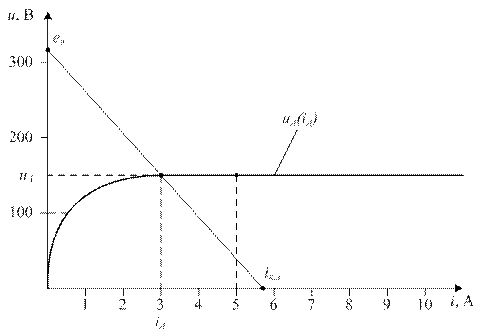рис. 26

По результатам графического расчета

,

Используя полученные значения тока и напряжения нелинейного элемента R_a по законам Кирхгофа для схемы рис. 19 находятся остальные токи и напряжения:

Узел ƒ:

Контур I:

Узел „:

Контур II:

4.2.2. Расчет установившегося режима до коммутации численным методом (с помощью решающего блока GIVEN…FIND системы MathCAD)

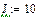
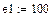
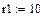
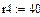
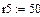
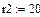
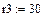
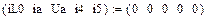
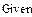
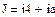
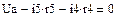
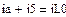
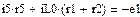
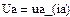
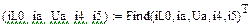
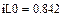
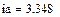
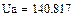
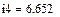
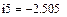
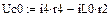
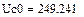
Результаты расчета схемы до коммутации графическим методом подтверждаются численным методом.

4.2.3. Расчет установившегося режима до коммутации численным методом с помощью принципа расщепления.

Одним из основных способов численного решения систем нелинейных алгебраических уравнений является итерационный способ последовательных приближений. Именно такая система получается при составлении расчетных уравнений Кирхгофа для схемы рис. 13. Основной «проблемой» итерационных методов решения нелинейных алгебраических систем является проблема сходимости итерационного процесса. В математической теории существуют оценки сходимости итерационных процессов при решении нелинейных САУ (систем алгебраических уравнений). Радиус сходимости матрицы коэффициентов САУ должен быть меньше единицы. Для обеспечения этого условия сходимости можно использовать так называемый принцип расщепления. Суть этого принципа заключается в выделении из слагаемого нелинейного элемента составляющей, определяемой максимальным статическим параметром этого НЭ. Так, для НЭА максимальный статический параметр – это максимальное статическое сопротивление R_A(0) при токе i_Aв нем равным нулю. Для НЭВ максимальный статический параметр – это максимальная статическая проводимость G_B(0) при напряжении u_B на нем равном нулю. Следует обратить внимание на то, что именно в этих случаях следует брать в качестве функции ВАХ, а что будет при этом аргументом ВАХ. Для НЭА при описании ВАХ в качестве функции следует брать напряжение u_A, а в качестве аргумента – ток i_A, то есть ВАХ НЭА: u_A(i_A). График u_A(i_A) имеет монотонно-выпуклый характер и нелинейное статическое сопротивление R_A этого НЭ имеет характеристику R_A(i_A) спадающего вида с максимальным сопротивлением R_Amax при . Для НЭВ при описании ВАХ в качестве функции следует брать ток i_B, в качестве аргумента – напряжение u_B. В этом случае график i_B(u_B) имеет выпуклый характер и статический параметр этого элемента – это проводимость G_B(u_B) с максимальным значением при .

Для рассматриваемой схемы (рис. 22) система нелинейных уравнений Кирхгофа имеет вид:

Нелинейное слагаемое в этой системе имеется в четвертом уравнении. Проведем «расщепление» этого слагаемого добавляя к нему максимальную составляющую, равную . При расщеплении нелинейного слагаемого его следует перенести в правую часть системы, а затем вычитать в правой и левой части уравнения максимальную составляющую, определяемую максимальным статическим параметром этого НЭ.

После такого «расщепления» система принимает вид.

После переноса нелинейного слагаемого в правую часть системы получим в левой части линейные слагаемые с постоянной матрицей коэффициентов A, в правой части нелинейную матрицу – столбец B.

iL

iA

i4

i5

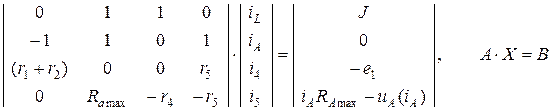
Итерационный процесс решения полученного матричного уравнения будет устойчив и сходится к решению.

В качестве начального приближения для неизвестных (i_L, i_A, i₄, i₅) можно задаться нулевыми значениями:

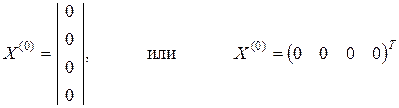
Итерационный процесс строится по формуле

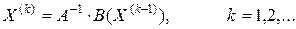
При достижении заданной точности ε

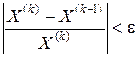
процесс останавливается и значение X^(k) считается решением САУ.

Реализация вышеописанного алгоритма проведена в системе MathCAD и приведена ниже.

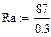
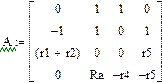
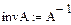
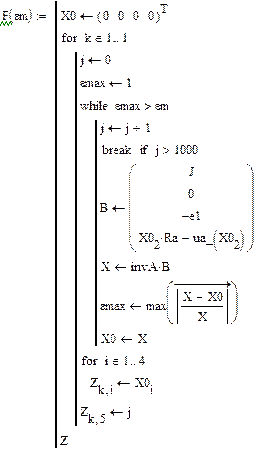
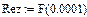
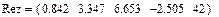
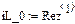
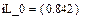
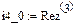
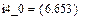
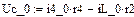
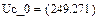
Результаты расчетов различными способами совпадают.

Независимые начальные условия (ННУ) для рассчитываемой схемы:

,

4.3. Расчет переходного процесса в цепи с постоянными источниками методом дискретных резистивных схем с применением принципа расщепления.

Для послекоммутационной нелинейной схемы (рис. 3) уравнения Кирхгофа имеют вид:

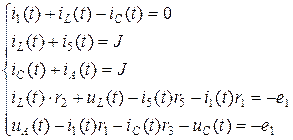(3)

При расчете численным методом составляется дискретная резистивная схема (рис. 27)

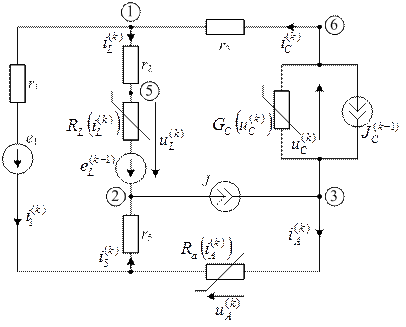рис. 27

Уравнения Кирхгофа для дискретного момента времени t_k этой схемы имеют вид:

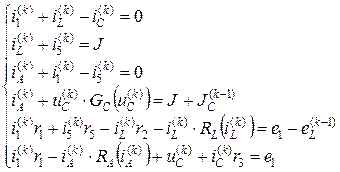
В полученной системе нелинейных алгебраических уравнений:

При численном решении уравнения по 2 закону Кирхгофа рекомендуется заменить уравнениями, связывающими потенциалы узлов схемы с токами. В результате получается система гибридных уравнений (индекс «k» для упрощения записи опущен)

На каждом шаге временной дискретизации Δt_k полученная система нелинейных алгебраических уравнений решается итерационным способом. Для обеспечения устойчивости итераций в системе следует провести расщепление нелинейных слагаемых.

Напряжение и исключим из системы.

Нелинейные напряжения и заменяются сплайновыми характеристиками и . Нелинейный ток i_C в емкости также представляется с помощью сплайновой характеристики нелинейной емкости

После расщепления система принимает вид

1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

В полученной системе все нелинейные слагаемые перенесены в правую часть системы.

Дополнительные дискретные источники:

,

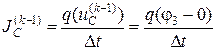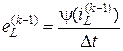
определяются по значениям i_L и u_C, вычисленным для предшествующего момента времени t_k-1.

В качестве неизвестных в записанной выше системе берутся: i_L, i_A, i_C, i₁, i₅, φ₁, φ₂, φ₃, φ₄, φ₅ – то есть десять неизвестных. Начальные условия для этих неизвестных, то есть их значения при находятся из решения нелинейной системы уравнений Кирхгофа (3), записанной при . Решение проведено с помощью процедуры GIVEN…FIND и приведено ниже.

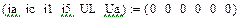
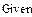
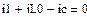
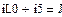
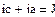
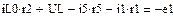
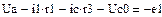
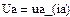
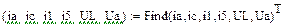
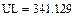
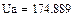
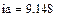
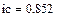
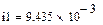
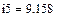
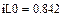
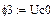
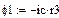
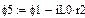
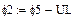
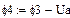
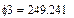
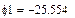
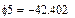
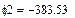
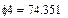
В матричной форме система решаемых уравнений имеет вид:

iL

iA

iC

i1

i5

φ1

φ2

φ3

φ4

φ5

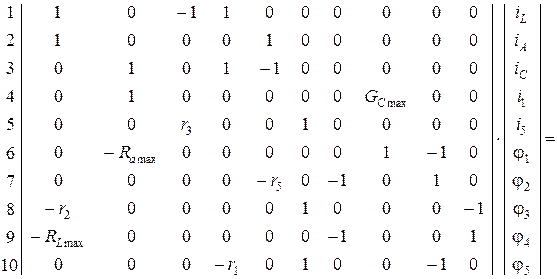
X01

X02

X03

X04

X05

X06

X07

X08

X09

X010

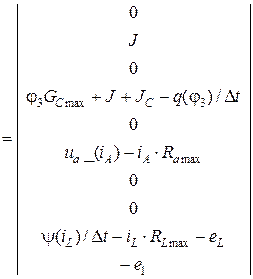
Реализация описанного алгоритма в системе MathCAD приведена ниже

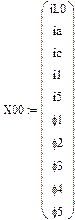
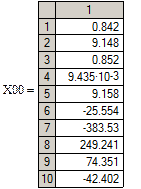
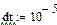
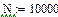
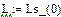
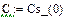
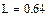
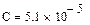
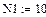
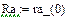
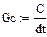
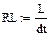
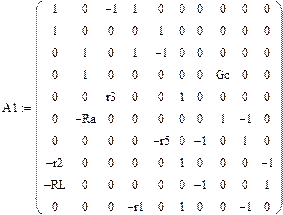
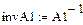
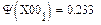
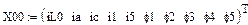
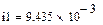
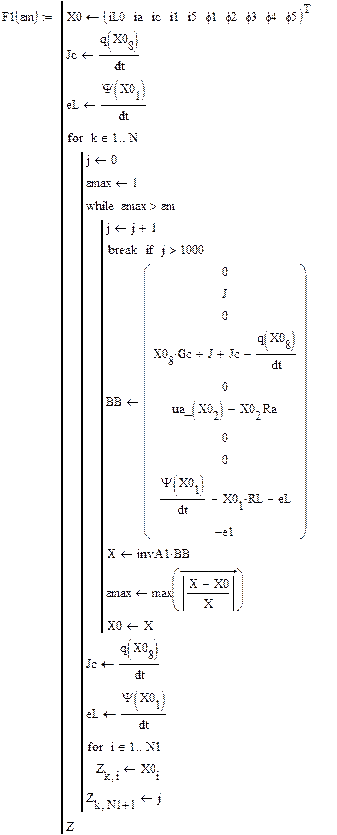
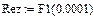
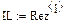
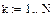
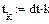
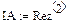
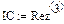
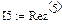
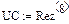
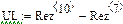
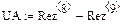
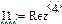
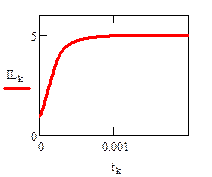
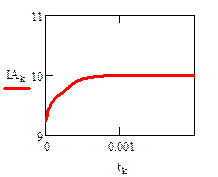
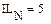
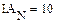
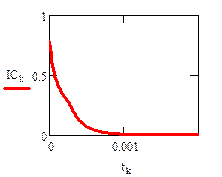
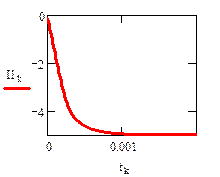
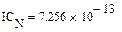
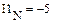
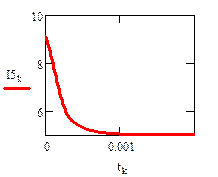
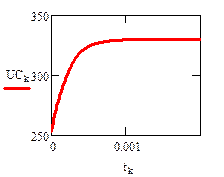
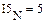
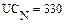
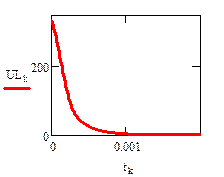
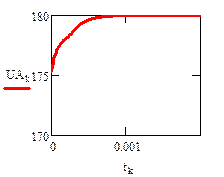
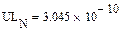
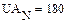
4.4. Расчет установившегося режима в схеме после коммутации (с помощью решающего блока GIVEN…FIND)

Схема в установившемся режиме имеет вид (рис. 28)

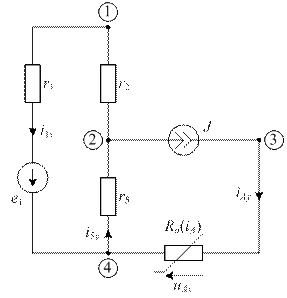рис. 28

Уравнения Кирхгофа в установившемся режиме имеют вид:

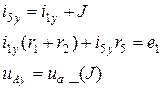
Реализация в системе MathCAD приведена ниже

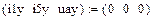
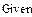
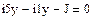
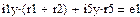
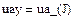
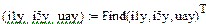
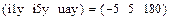
Результаты расчета установившегося режима в п.4.3 совпадают с расчетом в п.4.4.