Давление идеального газа пропорционально произведению концентра-ции молекул и средней кинетической энергии поступательного движения молекул
Тема. Температура и тепловое равновесие
ПовторениеКонец формыНачало формы
Запомни основное уравнение МКТ
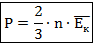
Давление идеального газа пропорционально произведению концентра-ции молекул и средней кинетической энергии поступательного движения молекул.
Или же:
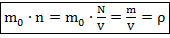 – плотность газа
– плотность газа
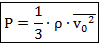 Конец формы
Конец формы
2. Температура как мера теплового равновесия
Как уже было сказано выше, понятие температура не является новым для нас. В восьмом классе мы определяли её как меру нагретости тела. Теперь же мы расширим это понятие. Ведь температура является очень важным макропараметром, который определяет величину теплового хаотического движения молекул и атомов.
Для начала вспомним, как нужно измерять температуру какого-либо тела. Мы приводим прибор для измерения температуры – термометр – в контакт с телом, температуру которого хотим замерить, и ждём некоторое время. Зачем мы это делаем? Чтобы температура тела и температура термометра стали одинаковыми (термометр способен показывать лишь свою температуру). Или же говорят, что термометр и тело находятся в состоянии теплового равновесия.
Тепловое равновесие – такое состояние тела, при котором его макроскопические параметры не меняются длительное время.
Так воттемпература – мера теплового равновесия тела или системы тел. И сведения о температурах двух тел дают нам представление о направлении перехода тепла – от более нагретого тела к менее нагретому.
Следует отметить, что наиболее распространённые в быту термометры – ртутные, спиртовые и т.д. (рис. 1) – не отвечают физическим стандартам измерения температур.

Рис. 1. Спиртовой и ртутный термометры соответственно
Причины этому две:
1. Различные термометры используют различные вещества в качестве индикатора, поэтому на одно и то же изменение температуры в зависимости от свойств конкретного вещества термометры реагируют по-разному;
2. Произвольность выбора начала отсчёта шкалы температур.
3. Недостатки термометров, газовые термометры
Поэтому для любых точных замеров температур такие термометры не годятся. И начиная с восемнадцатого века, используются более точные термометры, коими является газовые термометры (см. рис. 2)
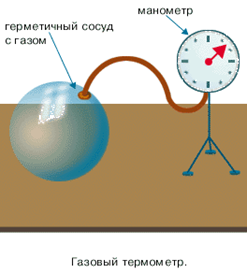
Рис. 2. Газовый термометр
Причиной этого является тот факт, что газы расширяются одинаково при изменении температуры на одинаковые значения. Для газовых термометров справедливо следующее:

То есть для измерения температуры либо фиксируется изменение давления при постоянном объёме, либо объём при постоянном давлении.
В газовых термометрах часто используют разреженный водород, который, как мы помним, очень хорошо подходит под модель идеального газа.
4. Абсолютная шкала температур
Кроме неидеальности бытовых термометров имеет место быть неидеальность многих шкал, которые используются в быту. В частности, шкала Цельсия, как наиболее нам знакомая. Как и в случае с термометрами эти шкалы выбирают случайным образом начальный уровень (для шкалы Цельсия это температура плавления льда). Поэтому для работы с физическими величинами необходима другая, абсолютная шкала.
Эту шкалу ввёл в 1848 г английский физик Уильям Томпсон (лорд Кельвин) (рис. 3). Зная, что при росте температур тепловая скорость движения молекул и атомов тоже растёт, нетрудно установить, что при уменьшении температур скорость будет падать и при определённой температуре рано или поздно станет нулём, как и давление (исходя и основного уравнения МКТ). Эту температуру и выбрали за начало отсчёта. Совершенно очевидно, что температура не может достигнуть значения меньше этого значения, поэтому оно получило название «абсолютный ноль температур». Для удобства же 1 градус по шкале Кельвина был приведён в соответствии с 1 градусом по шкале Цельсия.
Итак, получаем следующее:

Следовательно, абсолютный ноль температур – это температура
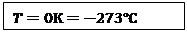

Рис. 3. Уильям Томсон
5. Температура как мера средней кинетической энергии поступательного движения молекул
Теперь для определения температуры как меры средней кинетической энергии молекул имеет смысл обобщить те рассуждения, которые мы приводили в определении абсолютной шкалы температур:
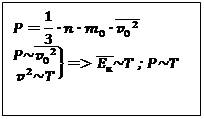
Итак, как видим, температура и правда является мерой средней кине-тической энергией поступательного движения. Конкретное же формульное соотношение вывел австрийский физик Людвиг Больцман (рис. 4):
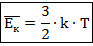
Здесь 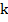 – так называемый коэффициент Больцмана. Это константа, численно равная:
– так называемый коэффициент Больцмана. Это константа, численно равная:
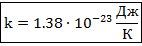
Как мы видим, размерность этого коэффициента – 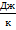 , то есть это своего рода коэффициент пересчёта из шкалы температур в шкалу энергий, ведь мы понимаем теперь, что, по сути, должны были измерять температуру в единицах энергии.
, то есть это своего рода коэффициент пересчёта из шкалы температур в шкалу энергий, ведь мы понимаем теперь, что, по сути, должны были измерять температуру в единицах энергии.
Теперь рассмотрим, как будет зависеть давление идеального газа от температуры. Для этого запишем основное уравнение МКТ в следующем виде:
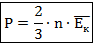
и подставим в эту формулу выражение для связи средней кинетической
энергии с температурой. Получим:
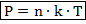

Рис. 4. Людвиг Больцман
Домашнее задание:
1. Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский. Классический курс. Физика. 10 класс, «Просвещение», 2014. Повторить §57-60 (с.188-203).
2. Конспектировать и учить лекционный материал.
