Линейного четырехполюсника

ОСНОВЫ ТЕОРИИ ЧЕТЫРЕХПОЛЮСНИКОВ

Ранее в качестве структурных элементов цепи рассматривались, в основном, пассивные и активные двухполюсники. При анализе радиотехнических устройств обработки сигналов часто бывает удобным вводить более сложные структурные элементы, к которым относятся, прежде всего, четырехполюсники.

По определению четырехполюсником называют элемент цепи, имеющий две пары внешних полюсов (зажимов). Внутреннее устройство четырехполюсника может быть любым. Поэтому иногда говорят, что данный элемент цепи представляет собой «черный ящик».

В схемах четырехполюсников на рис. 5.1 выделены две пары внешних зажимов (полюсов): 1 и 2. Зажимы, к которым подключается внешний источник воздействия (колебаний), называются входными, а зажимы, к которым присоединяется приемник (нагрузка), – выходными зажимами.

В качестве примеров четырехполюсников можно привести трансформатор, усилитель, фильтр и др. Все эти устройства, имеющие совершенно «непохожие» схемы, обладают рядом общих свойств.

ОСНОВНЫЕ УРАВНЕНИЯ И ПЕРВИЧНЫЕ ПАРАМЕТРЫ

ЛИНЕЙНОГО ЧЕТЫРЕХПОЛЮСНИКА

Электрическое состояние линейного четырехполюсника задается комплексными амплитудами напряжений Ú₁и Ú₂ и токов Ì₁и Ì₂. В зависимости от особенностей решаемой задачи положительные направления токов Ì₁и Ì₂ выбираются одним из способов, показанных на рис. 5.1, а, б.

Из четырех указанных величин любые две могут рассматриваться как независимые. Тогда оставшиеся величины связаны системой двух линейных алгебраических уравнений. Конкретный выбор независимых переменных приводит к различным системам уравнений, которые называют основными уравнениями четырехполюсников.Коэффициенты в них называют первичными параметрами. Всего возможно шесть таких систем (число сочетаний из четырех по два). На практике чаще всего применяют четыре системы уравнений.

Система Z-параметров. Здесь независимыми переменными служат комплексные амплитуды Ì₁и Ì₂, так что основные уравнения приобретают вид

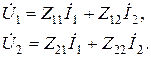(5.1)

Коэффициенты уравнений (5.1) образуют Z-матрицу четырехполюсника

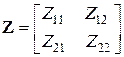. (5.2)

Z-параметры являются в общем случае комплексными величинами, зависящими от частоты. Матрица Z служит полной математической моделью линейного стационарного четырехполюсника.

Z-параметры имеют физическую размерность сопротивления. Их можно найти экспериментально в режиме холостого хода на выходе (Ì₂ = 0) и на входе (Ì₁ = 0), так как на основании уравнений (5.1)

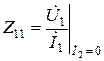– входное сопротивление в режиме холостого хода на выходе;

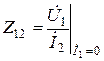– взаимное сопротивление обратной передачи (по направлению от зажимов 2 к зажимам 1) при разомкнутых зажимах 1;

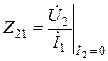– взаимное сопротивление прямой передачи (по направлению от зажимов 1 к зажимам 2) при разомкнутых зажимах 2;

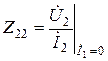– выходное сопротивление в режиме холостого хода на входе;

Система Y-параметров. Получается в том случае, когда независимыми переменными выбраны напряжения на входе и выходе. При этом состояние четырехполюсника определяется двумя линейными алгебраическими уравнениями

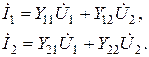(5.3)

Матрица из четырех комплексных коэффициентов

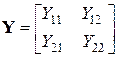(5.4)

называется Y-матрицей четырехполюсника. Элементы этой матрицы имеют размерность проводимости. Их можно найти таким же образом, как это описывалось применительно к Z-параметрам, в режимах короткого замыкания на выходе (Ú₂ = 0) и на входе (Ú₁ = 0). Например,

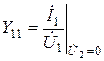– входная проводимость в режиме короткого замыкания на выходе.

Система H-параметров. Здесь независимыми переменными являются Ì₁, и Ú₂ , а функциями - Ú₁ и Ì₂:

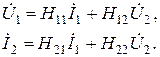(5.5)

Матрицу

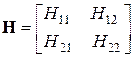(5.6)

называют H-матрицей линейного четырехполюсника. Физическая интерпретация элементов матрицы раскрывается в режиме короткого замыкания на выходе (Ú₂ = 0) и холостого хода на входе (Ì₁ = 0):

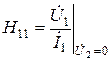– входное сопротивление в режиме короткого замыкания на выходе;

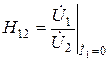– безразмерный коэффициент передачи по напряжению в обратном направлении (от полюсов 2 к полюсам 1) в режиме холостого хода на входе;

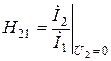– безразмерный коэффициент передачи по току в прямом направлении при коротком замыкании выходных зажимов;

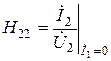– выходная проводимость при разомкнутом входе.

Система A-параметров. Отличается тем, что в качестве независимых переменных принимаются комплексные амплитуды напряжения и тока на выходных зажимах, причем выходной ток Ì₂ (рис. 5.2) направлен из четырехполюсника (в отличие от других систем параметров)

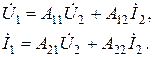(5.7)

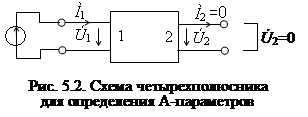Для определения физического смысла A-параметров из системы уравнений (5.7) нужно к входным полюсам подключить источник сигнала, а на выходных полюсах создать режимы холостого хода и короткого замыкания (рис. 5.2). На основании этих опытов получим:

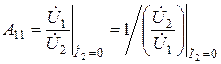– величина, обратная коэффициенту передачи по напряжению в прямом направлении в режиме холостого хода на выходе;

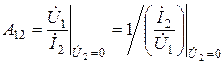– величина с размерностью сопротивления, обратная взаимной проводимости между выходными и входными полюсами в режиме короткого замыкания на выходе;

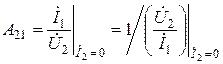– величина с размерностью проводимости, обратная взаимному сопротивлению между выходными и входными полюсами в режиме холостого хода на выходе;

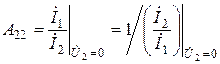– величина, обратная коэффициенту передачи по току в прямом направлении в режиме короткого замыкания на выходе.