Системы линейных уравнений.
Алгебра матриц
1. Линейные действия с матрицами. Транспонирование.Квадратной матрицей порядка 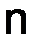 называется таблица из
называется таблица из 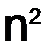 чисел
чисел 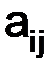 , расположенных в
, расположенных в 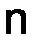 строк и
строк и 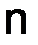 столбцов:
столбцов:
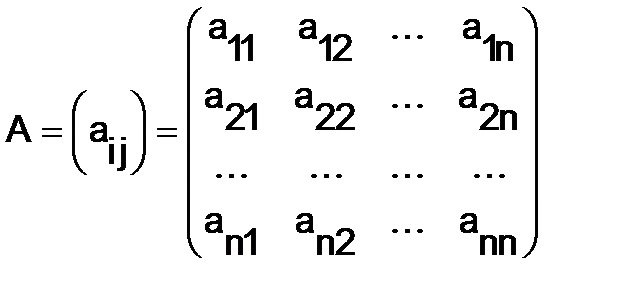 (1)
(1)
Первый индекс i у элемента 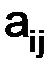 означает номер строки, второй индекс j – номер столбца, в которых стоит этот элемент. Диагональ
означает номер строки, второй индекс j – номер столбца, в которых стоит этот элемент. Диагональ 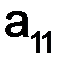
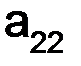

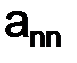 называется главной диагональю матрицы
называется главной диагональю матрицы  .
.
Две матрицы 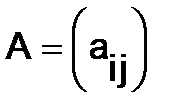 и
и 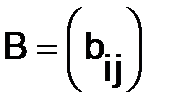 одного и того же порядка считаются равными, если все соответствующие их элементы равны, т.е.
одного и того же порядка считаются равными, если все соответствующие их элементы равны, т.е. 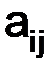 =
= 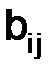
(i, j = 1,2 …,n). Матрицы разных порядков не сравниваются между собою.
Линейными преобразованиями над матрицами называются сложение матриц и умножение их на число. Оба этих действия определяются поэлементно:
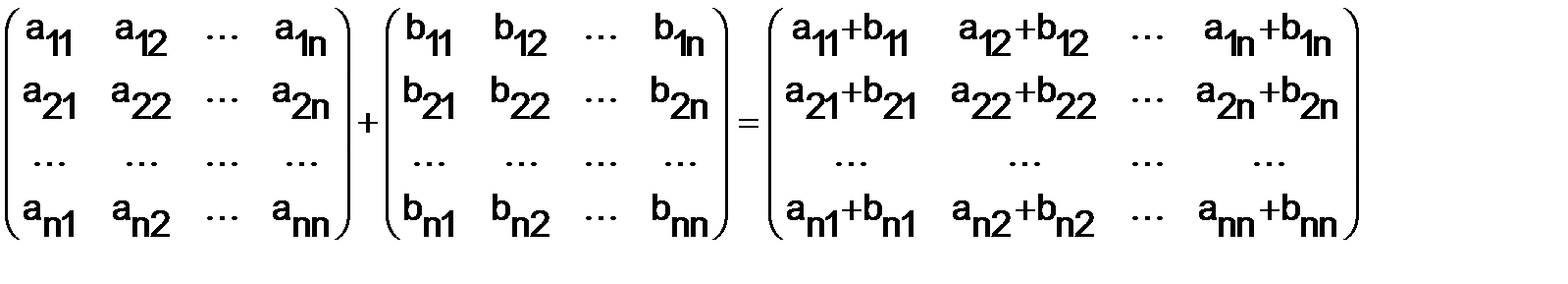 ,
,
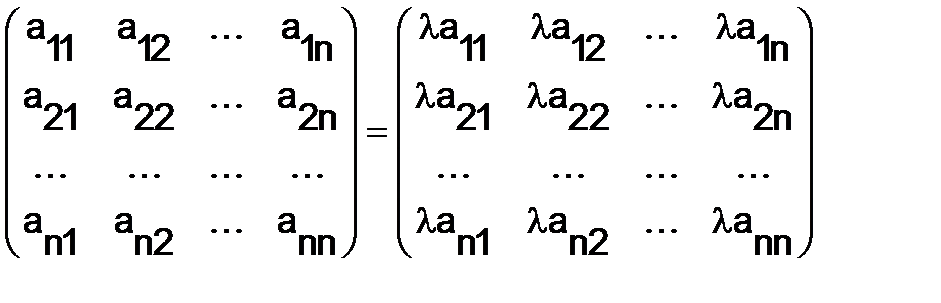 .
.
Свойства сложения матриц и умножения их на число:
1) 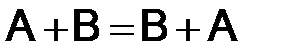
2) 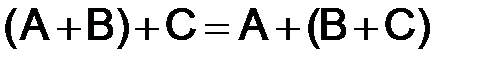
3) 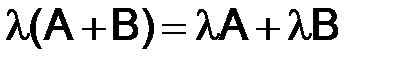 (2)
(2)
4) 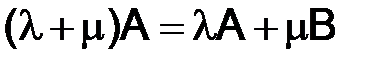
5) 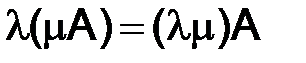
Матрица 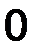 , целиком состоящая из нулей, называется нулевой, для неё
, целиком состоящая из нулей, называется нулевой, для неё 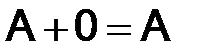 .
.
Сложение матриц имеет обратное действие – вычитание, которое также осуществляется поэлементно, например если 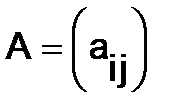 ,
, 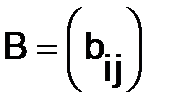 , то
, то
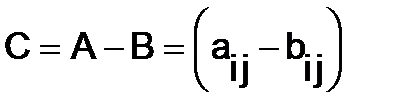
Операция над матрицей  , при которой её строки становятся столбцами с теми же номерами, а столбцы – строками, называется транспонированием и обозначается
, при которой её строки становятся столбцами с теми же номерами, а столбцы – строками, называется транспонированием и обозначается 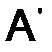 . Например, если
. Например, если
 , то
, то  .
.
Операция транспонирования обладает следующими свойствами:
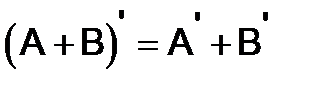 ,
, 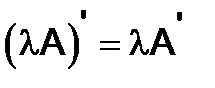 ,
, 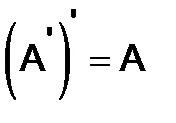 . (3)
. (3)
Матрица, у которой все элементы, не стоящие на главной диагонали , равны нулю, называется диагональной.
Матрица 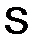 называется симметрической, если она не меняется при транспонировании, т.е.
называется симметрической, если она не меняется при транспонировании, т.е. 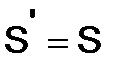 . У симметрической матрицы элементы, симметричные относительно главной диагонали, равны. Матрица
. У симметрической матрицы элементы, симметричные относительно главной диагонали, равны. Матрица 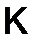 называется кососимметрической , если при транспонировании она меняет свой знак, т.е.
называется кососимметрической , если при транспонировании она меняет свой знак, т.е. 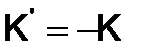 . У кососимметрической матрицы на главной диагонали стоят нули, а элементы, симметричные относительно этой диагонали, отличаются только знаком.
. У кососимметрической матрицы на главной диагонали стоят нули, а элементы, симметричные относительно этой диагонали, отличаются только знаком.
Определитель, составленный из элементов матрицы n-го порядка (1), называется определителем матрицы  и обозначается
и обозначается  .
.
264.Пусть 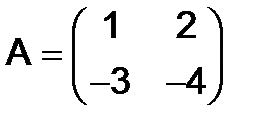 ,
, 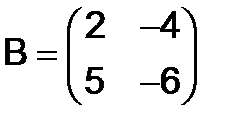 . Найти
. Найти 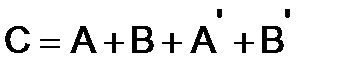
Решение . Пользуясь сочетательным и переместительным свойствами сложения матриц, имеем
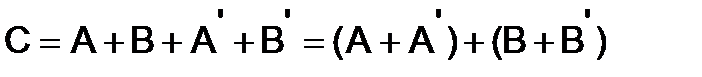 ,
,
Но
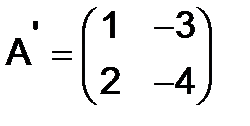 ,
, 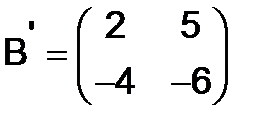 ,
,
Поэтому
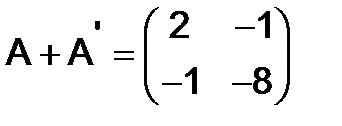 ,
, 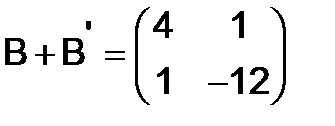 и
и
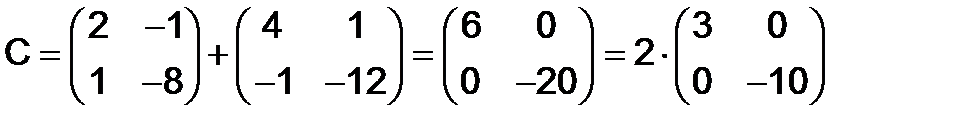 .
.
Полученная матрица  представляет пример диагональной матрицы второго порядка.
представляет пример диагональной матрицы второго порядка.
265.Показать, что матрица 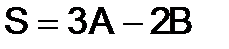 - симметрическая, если
- симметрическая, если
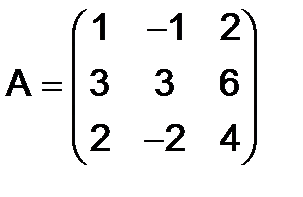 и
и 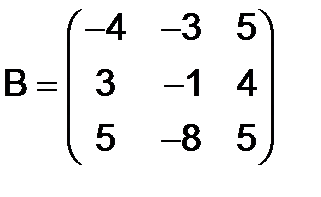 .
.
Решение. Имеем
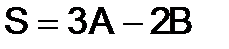 =
= 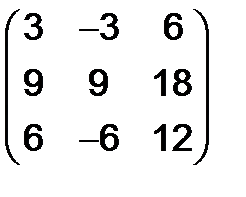
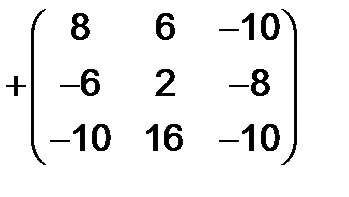
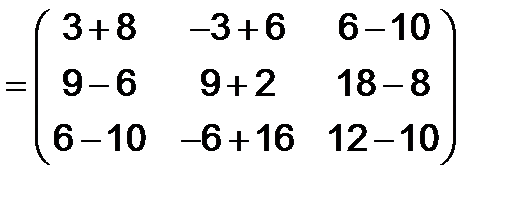
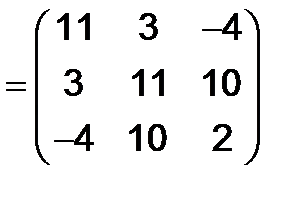 .
.
Ясно, что полученная матрица S - симметрическая, так как она не меняется при транспонировании.
266.Показать, что матрица  - кососимметрическая, если
- кососимметрическая, если
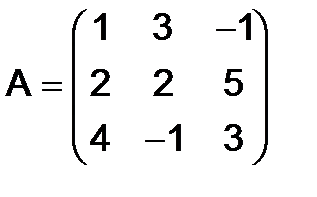 и
и 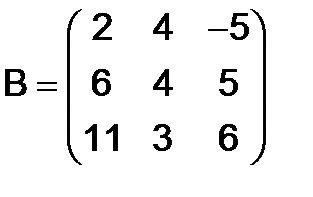
Решение. Имеем

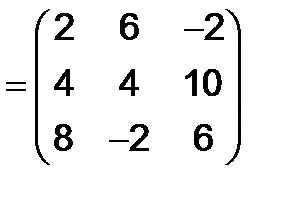
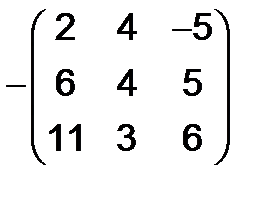
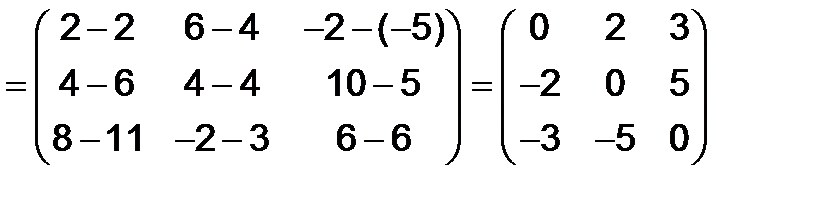 .
.
Так как 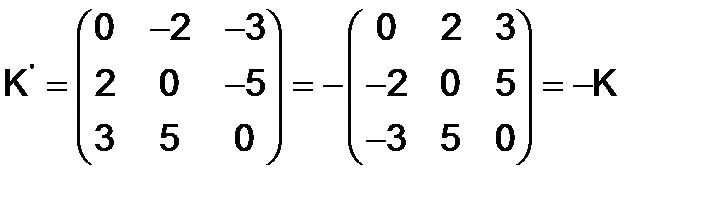 , то матрица
, то матрица 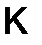 является кососимметрической.
является кососимметрической.
267.Доказать, что для любой матрицы  матрица
матрица 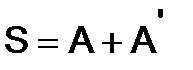 симметрическая.
симметрическая.
Решение. Применяя свойства (3) транспонирования, получим равенство 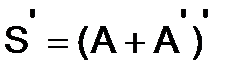
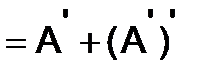
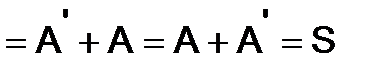 , т.е.
, т.е. 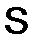 - симметрическая матрица.
- симметрическая матрица.
268.Показать , что для матрицы n-го порядка  выполняется равенство
выполняется равенство
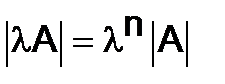 .
.
Решение. При умножении матрицы  на число
на число 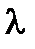 все её элементы умножаются на
все её элементы умножаются на 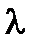 . Вынося этот множитель из каждой строки за знак определителя (см. свойство 3, § 1, п.2), получим требуемое равенство.
. Вынося этот множитель из каждой строки за знак определителя (см. свойство 3, § 1, п.2), получим требуемое равенство.
269.Найти 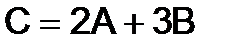 , если
, если 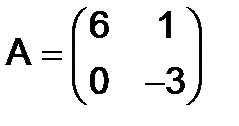 ,
, 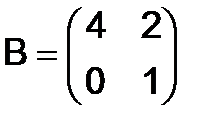 .
.
270.Найти матрицу 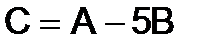 , если
, если 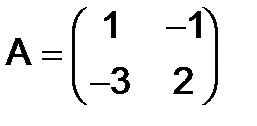 ,
, 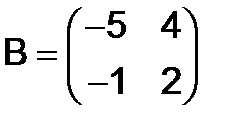 .
.
271.Найти матрицу 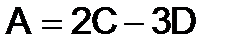 , если
, если
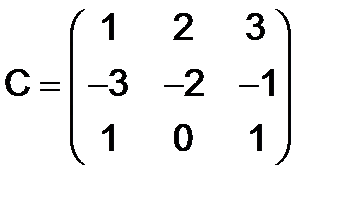 ,
, 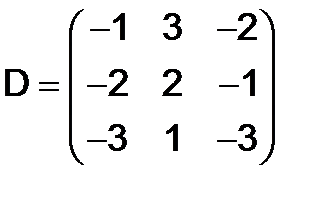 .
.
272.Показать, что матрица 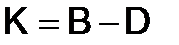 - кососимметрическая, если
- кососимметрическая, если
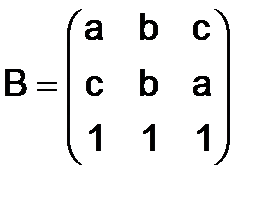 ,
, 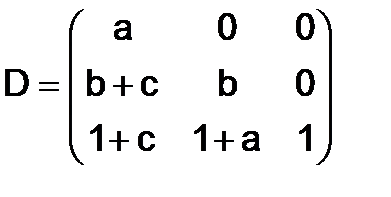 .
.
273.Показать, что матрица 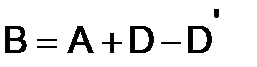 является нулевой матрицей, если
является нулевой матрицей, если
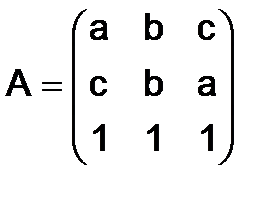 ,
, 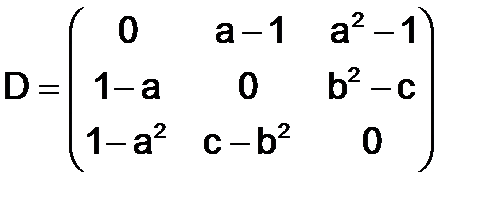 .
.
274.Показать, что для любой матрицы  матрица
матрица 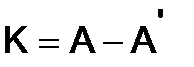 - кососимметрическая .
- кососимметрическая .
Указание. Стр. 267.
275.Дана произвольная матрица  , показать, что она может быть представлена в виде суммы симметрической и кососимметрической матриц.
, показать, что она может быть представлена в виде суммы симметрической и кососимметрической матриц.
Указание. Рассмотреть матрицы 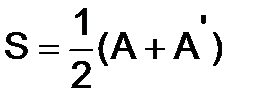 и
и 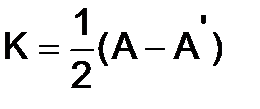 .
.
276.Выписать общий вид симметрической и кососимметрической матриц второго и третьего порядка. Найти их определители.
2. Умножение матриц.Произведение матрицы  на матрицу
на матрицу 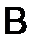 (того же порядка) определяется следующим образом: для того, чтобы получить элемент
(того же порядка) определяется следующим образом: для того, чтобы получить элемент 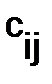 - матрицы произведения
- матрицы произведения 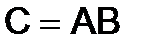 , надо элементы i-ой строки матрицы
, надо элементы i-ой строки матрицы  умножить на соответствующие элементы j-го столбца матрицы
умножить на соответствующие элементы j-го столбца матрицы 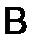 и результаты сложить, т.е.
и результаты сложить, т.е.
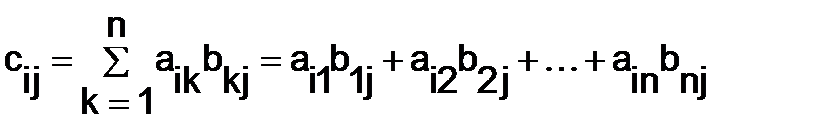 , (4)
, (4)
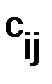 - произведение i-й строки матрицы
- произведение i-й строки матрицы  на j-й столбец матрицы
на j-й столбец матрицы 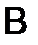 .
.
Свойства.
1) 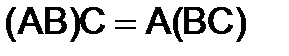 .
.
2) 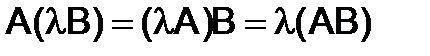 .
.
3) 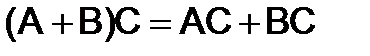 . (5)
. (5)
4) 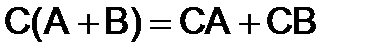 .
.
5) 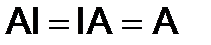 ,
,
где
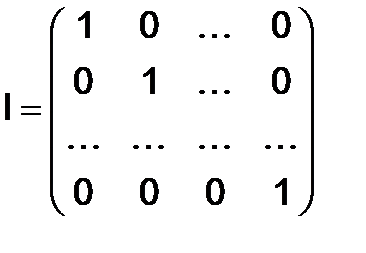 - единичная матрица.
- единичная матрица.
6)  ,
, 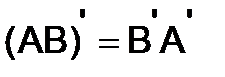 ,
, 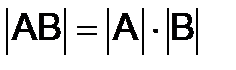 (6)
(6)
Заметим, что в общем случае 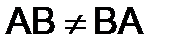 , т.е. умножение матриц не обладает коммутативным свойством, поэтому всегда надо строго следить за порядком множителей. Матрицы, для которых выполняется равенство
, т.е. умножение матриц не обладает коммутативным свойством, поэтому всегда надо строго следить за порядком множителей. Матрицы, для которых выполняется равенство 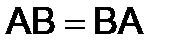 , называются перестановочными.
, называются перестановочными.
277.Найти произведение строки 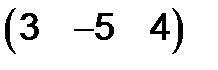 на столбец
на столбец 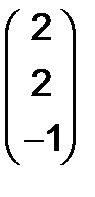 .
.
Решение. Надо перемножить соответственные элементы и сложить результаты:
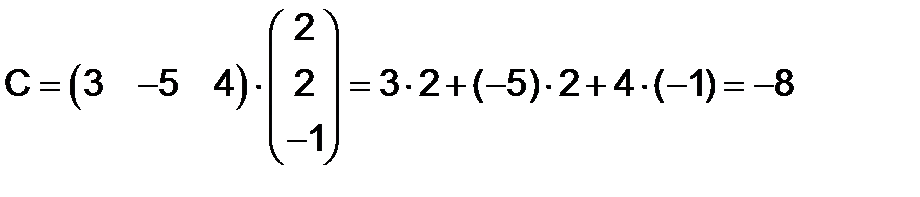 .
.
278.Найти произведения  и
и  матриц:
матриц:
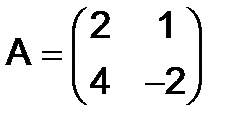 и
и 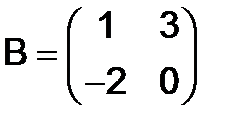 .
.
Установить, что матрицы  и
и 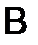 неперестановочны.
неперестановочны.
Решение. Пусть 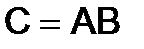 . Чтобы найти элемент
. Чтобы найти элемент 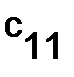 , надо умножить первую строку матрицы
, надо умножить первую строку матрицы  на первый столбец матрицы
на первый столбец матрицы 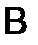 :
:
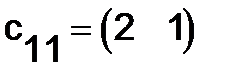

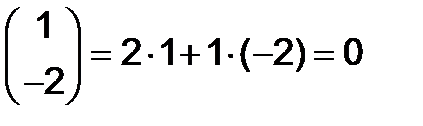
Элемент 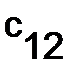 произведения
произведения  получается умножением первой строки
получается умножением первой строки  на второй столбец
на второй столбец 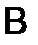 :
:
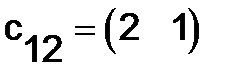

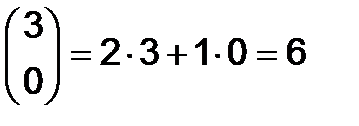
Аналогично, умножая вторую строку  на столбцы
на столбцы 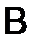 , найдём:
, найдём:
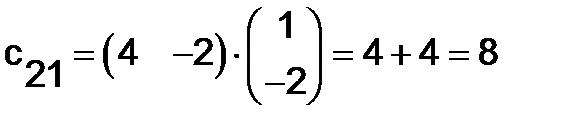 ;
; 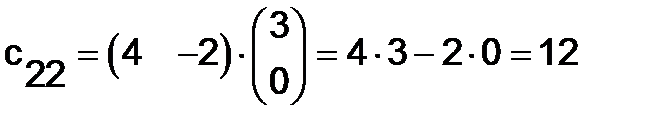
Таким образом,
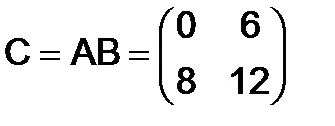 . Умножая теперь строки
. Умножая теперь строки 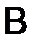 на столбцы
на столбцы  , получим (проверьте!)
, получим (проверьте!)
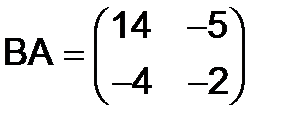 .
.
Так как 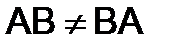 , то данные матрицы неперестановочны.
, то данные матрицы неперестановочны.
279.Найти произведение  данных матриц третьего порядка:
данных матриц третьего порядка:
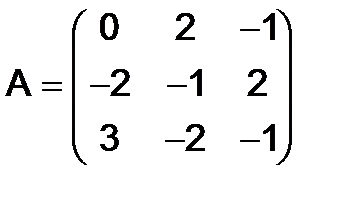 ,
, 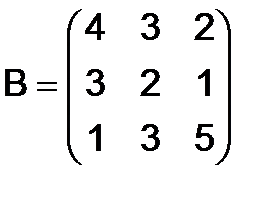 .
.
Решение. Умножив по очереди строки матрицы  на столбцы
на столбцы 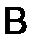 , получим
, получим
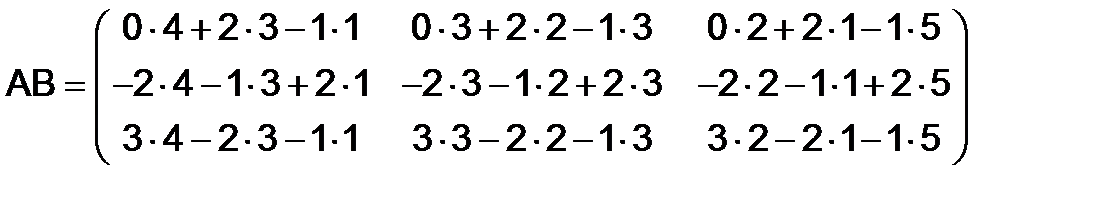
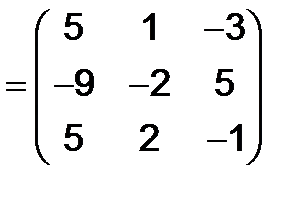 .
.
280.Найти все матрицы, перестановочные с 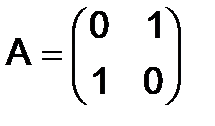 .
.
Решение. Пусть 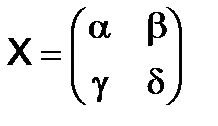 - искомая матрица , тогда
- искомая матрица , тогда 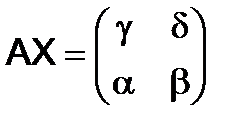 ,
, 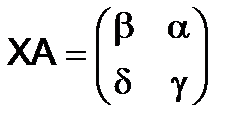 , и равенство
, и равенство 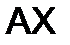
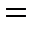
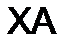 соблюдается тогда и только тогда, когда
соблюдается тогда и только тогда, когда 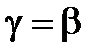 ,
, 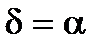 .
.
Таким образом, общий вид матрицы, перестановочной с данной матрицей  следующий:
следующий:
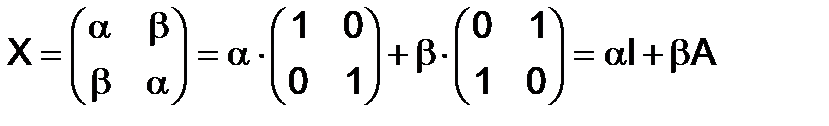 .
.
281.Показать, что произведение матрицы  на транспонированную всегда является симметрической матрицей.
на транспонированную всегда является симметрической матрицей.
282.Матрица  называется ортогональной, если выполняется условие
называется ортогональной, если выполняется условие
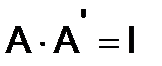 , или
, или 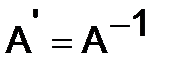 . Доказать, что матрица
. Доказать, что матрица  - ортогональная, если
- ортогональная, если
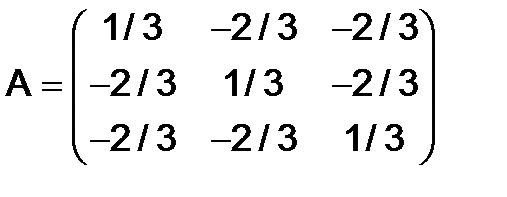 .
.
Решение. Из симметричности матрицы  следует, что
следует, что 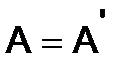 , поэтому
, поэтому
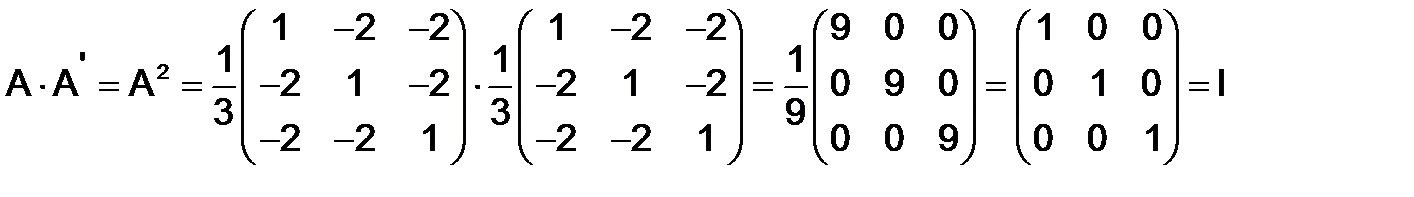
283.Произвести умножение квадратных матриц в следующих примерах:
а) 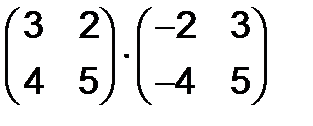 , б)
, б) 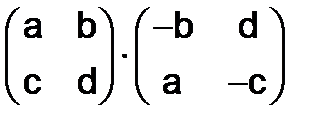 ,
,
в) 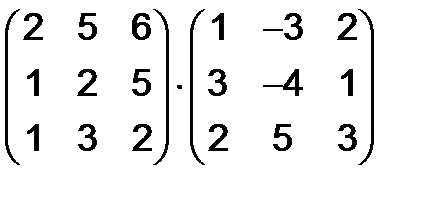 , г)
, г) 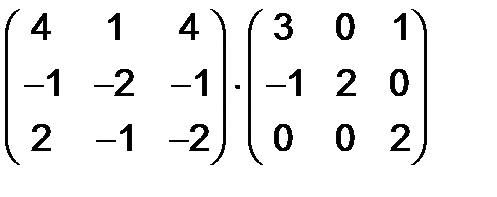 .
.
284.Показать, что матрицы  и
и 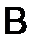 - перестановочны, если
- перестановочны, если
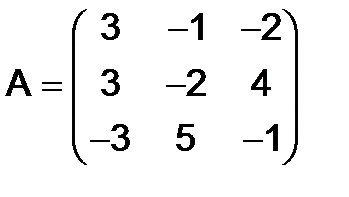 ,
, 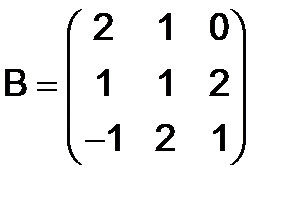 .
.
285.Найти матрицу 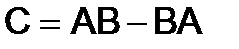 , если
, если
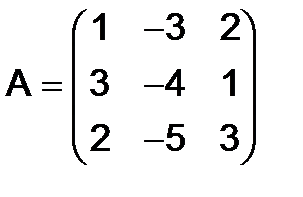 ,
, 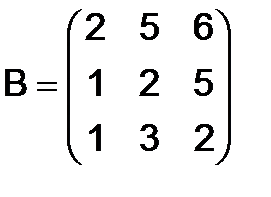 .
.
286.Показать, что матрицы
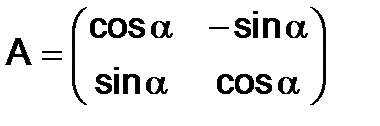 ,
, 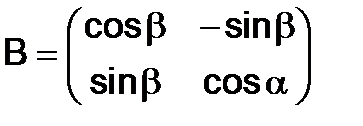 перестановочны.
перестановочны.
Найти их произведение.
287.Найти все матрицы, перестановочные с данными:
а) 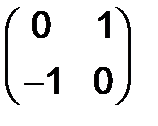 , б)
, б) 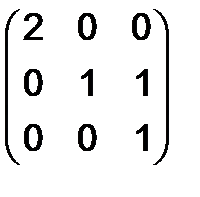 , в)
, в) 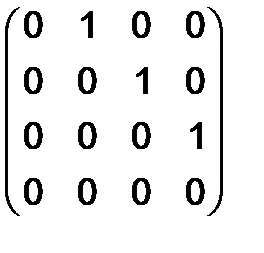 .
.
288.Найти общий вид матрицы  третьего порядка , для которой
третьего порядка , для которой
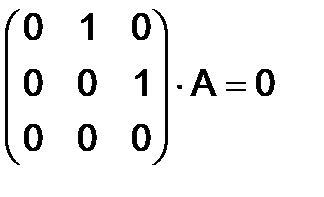 .
.
289.Ненулевые матрицы  и
и 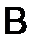 , для которых
, для которых 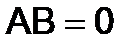 , называются делителями нуля. Показать, что определитель хотя бы у одной из этих матриц равен нулю.
, называются делителями нуля. Показать, что определитель хотя бы у одной из этих матриц равен нулю.
Указание. Использовать свойство умножения матриц (6).
290.Показать на примере матриц второго порядка , что равенство  невозможно.
невозможно.
3.Степени матриц. Многочлены от матриц.Целая неотрицательная степень матрицы определяется равенством:
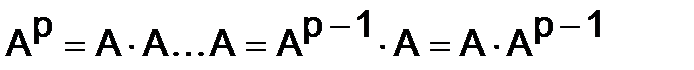 и
и 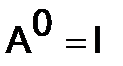 .
.
p раз
Для произведения степеней матриц справедливо равенство:
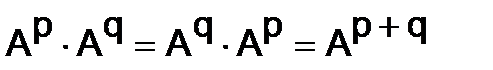 (p, q = 0, 1, 2, …)
(p, q = 0, 1, 2, …)
Если дан многочлен 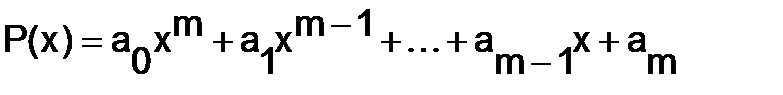 , то многочленом от матрицы
, то многочленом от матрицы  называется матрица
называется матрица 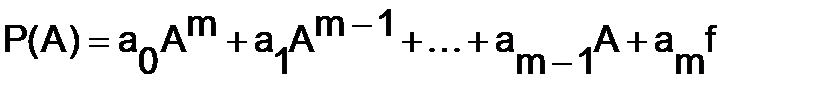 .
.
Всякие два многочлена о матрицы  перестановочны :
перестановочны :
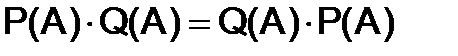 .
.
Если 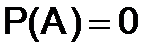 (нулевая матрица), то матрица
(нулевая матрица), то матрица  называется корнем многочлена.
называется корнем многочлена.
291.Найти 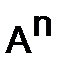 для матрицы
для матрицы 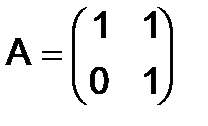 .
.
Решение. Вычисляем последовательно произведения по формуле (3):
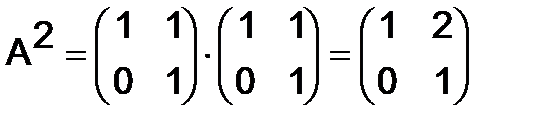 ,
, 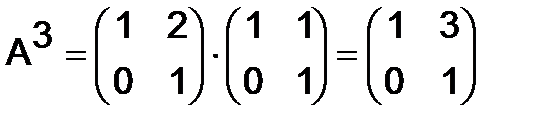 ,
,
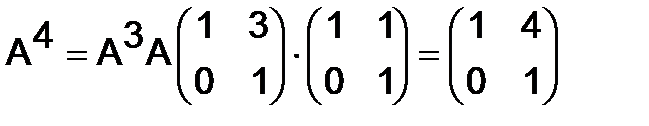 и т.д.
и т.д.
Продолжая умножение, придём к формуле:
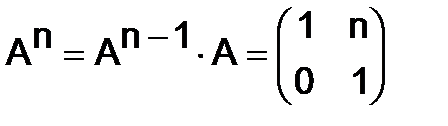 .
.
292.Матрица 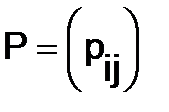 , у которой все элементы неотрицательны
, у которой все элементы неотрицательны 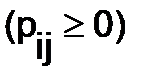 , а сумма элементов каждой строки равна единице, т.е.
, а сумма элементов каждой строки равна единице, т.е. 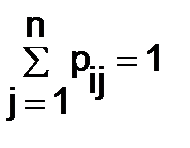 (i = 1, 2, …, n), называется матрицей переходных вероятностей или стохастической матрицей. Найти
(i = 1, 2, …, n), называется матрицей переходных вероятностей или стохастической матрицей. Найти 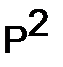 и
и 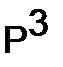 стохастической матрицы
стохастической матрицы
 .
.
Решение. Находим 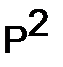 и
и 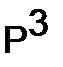 (предварительно за знак матрицы выносится общий множитель
(предварительно за знак матрицы выносится общий множитель 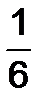 ):
):
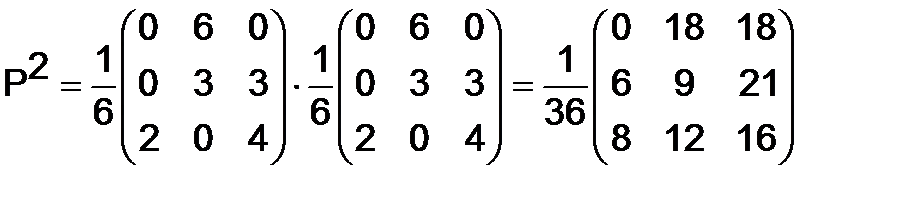 ,
,
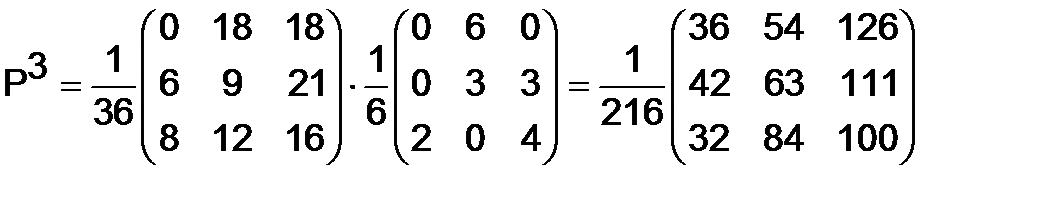 .
.
Заметим, что матрицы 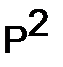 и
и 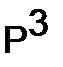 также являются стохастическими матрицами; вообще можно показать, что любая степень стохастической матрицы также является стохастической матрицей.
также являются стохастическими матрицами; вообще можно показать, что любая степень стохастической матрицы также является стохастической матрицей.
293.Найти все степени матрицы 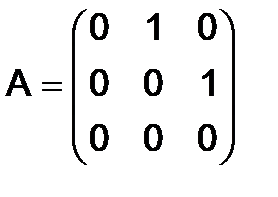 .
.
Решение. Имеем: 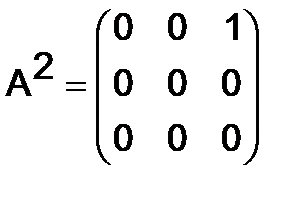 ,
, 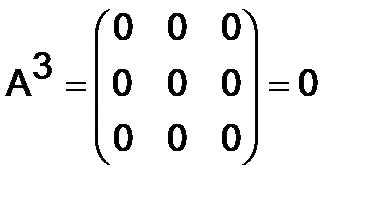 .
.
Значит, 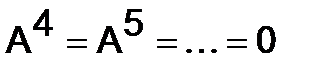 .
.
Ненулевая матрица  , для которой
, для которой 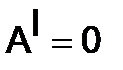 при некотором значении
при некотором значении 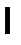 , называется нильпотентной. Наименьшее из числе
, называется нильпотентной. Наименьшее из числе 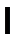 , для которых
, для которых 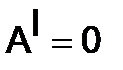 , называется показателем (индексом) нильпотентности . В этом примере
, называется показателем (индексом) нильпотентности . В этом примере 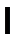 = 3.
= 3.
294.Найти многочлен от матрицы  , если
, если 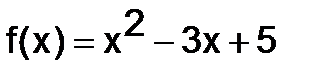 , а
, а
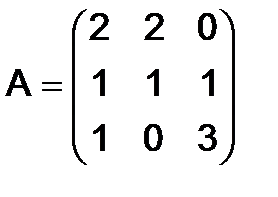 .
.
Решение. Искомая матрица 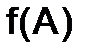 определяется равенством:
определяется равенством:
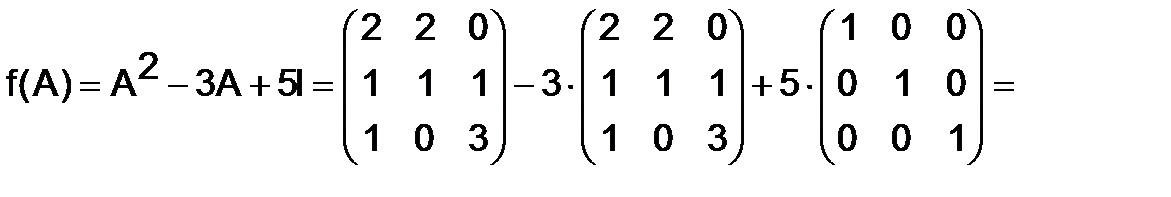
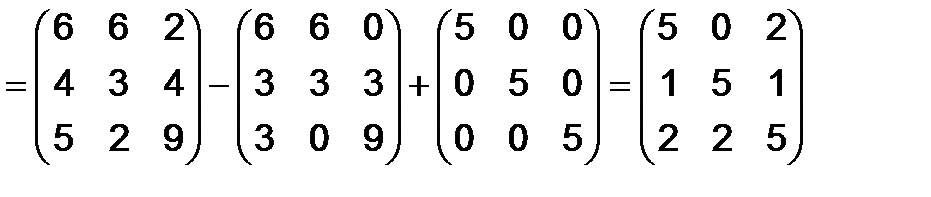 .
.
295.Показать, что матрица 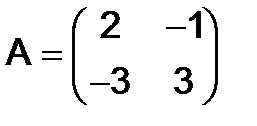 - корень многочлена
- корень многочлена 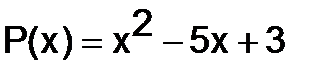 .
.
Решение. Имеем
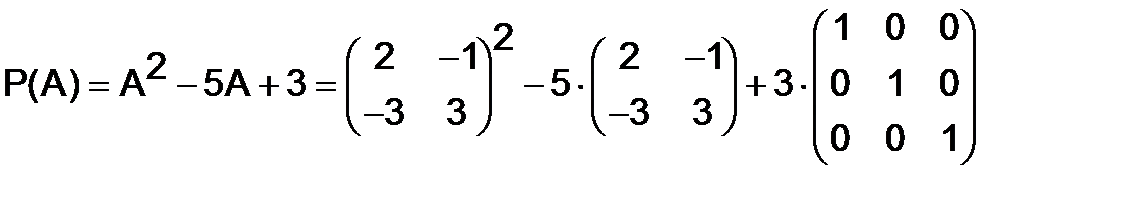
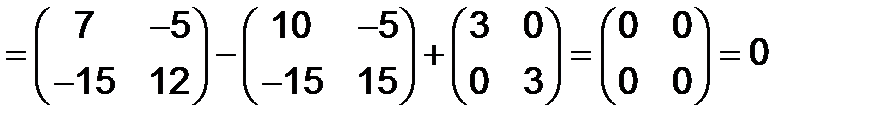 .
.
Т.е.  - корень многочлена
- корень многочлена 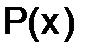 .
.
296.Найти 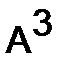 для следующих матриц:
для следующих матриц:
а) 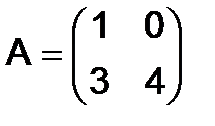 , б)
, б) 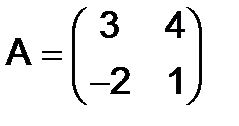 , в)
, в) 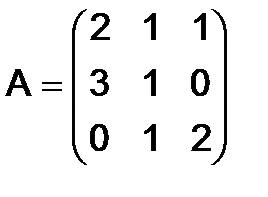 .
.
297.Найти все степени матриц 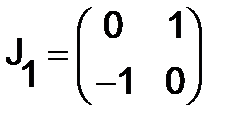 и
и 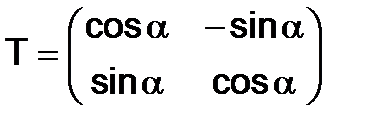 .
.
298.Матрица  называется инволютивной, если
называется инволютивной, если 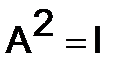 и идемпотентной, если
и идемпотентной, если 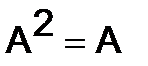 . Найти общий вид инволютивной и идемпотентной матрицы второго порядка.
. Найти общий вид инволютивной и идемпотентной матрицы второго порядка.
299.Найти 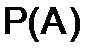 , если:
, если:
а) 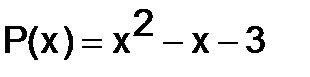 ,
, 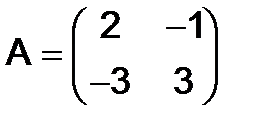 ; б)
; б) 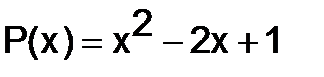 ,
, 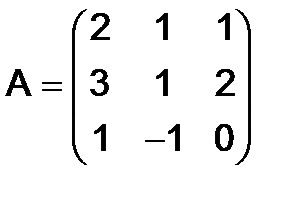 ;
;
в) 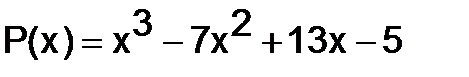 ,
, 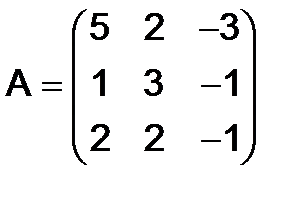 .
.
300.Найти общий вид матриц второго порядка, квадрат которых равен нулевой матрице, т.е 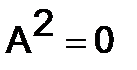 .
.
301.Найти все матрицы  второго порядка, квадрат которых равен диагональной матрице
второго порядка, квадрат которых равен диагональной матрице 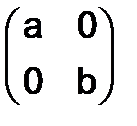 ,
, 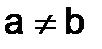 .
.
302.Найти условие, при котором матрица  второго порядка перестановочна со всеми матрицами второго порядка .
второго порядка перестановочна со всеми матрицами второго порядка .
303.Каким условиям должны удовлетворять элементы матрицы  второго порядка, для того, чтобы она была перестановочна со всеми диагональными матрицами того же порядка?
второго порядка, для того, чтобы она была перестановочна со всеми диагональными матрицами того же порядка?
4.Обратная матрица .Матрица 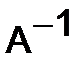 называется обратной матрице
называется обратной матрице  , если
, если 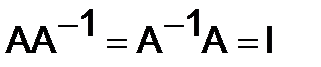 . Для того, чтобы матрица
. Для того, чтобы матрица  имела обратную матрицу, необходимо и достаточно, чтобы она была невырожденной , т.е. чтобы
имела обратную матрицу, необходимо и достаточно, чтобы она была невырожденной , т.е. чтобы 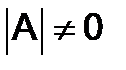 . Обратная матрица определяется по формуле
. Обратная матрица определяется по формуле
 , (7)
, (7)
где 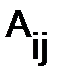 - алгебраические дополнения элементов
- алгебраические дополнения элементов 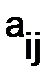 в определителе
в определителе  . Алгебраические дополнения для строчек матрицы
. Алгебраические дополнения для строчек матрицы  записываются в столбцы матрицы (7). Так, например, в первом столбце этой матрицы стоят алгебраические дополнения первой строки матрицы
записываются в столбцы матрицы (7). Так, например, в первом столбце этой матрицы стоят алгебраические дополнения первой строки матрицы  .
.
С помощью обратной матрицы решаются матричные уравнения вида:
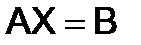 и
и 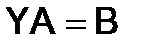 (при
(при 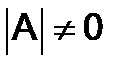 .) (8)
.) (8)
Умножая первое уравнение на 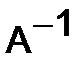 слева, а второе на
слева, а второе на 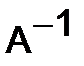 справа, получим их решение в виде:
справа, получим их решение в виде:
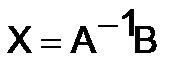 и
и  . (9)
. (9)
Свойства.
1) 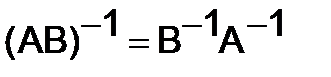 .
.
2) 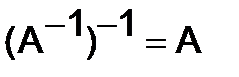 . (10)
. (10)
3) 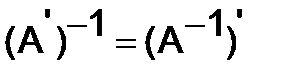 .
.
4) 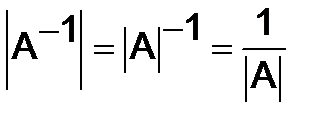 .
.
304.Найти обратную матрицу 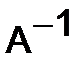 для матрицы
для матрицы 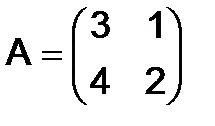 .
.
Решение. Покажем сначала, что данная матрица невырожденная, тогда она имеет обратную матрицу. Действительно,
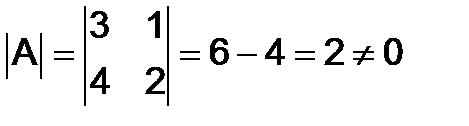 .
.
Вычислим алгебраические дополнения элементов матрицы :
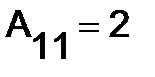 ,
, 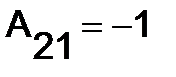 ,
, 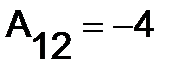 ,
, 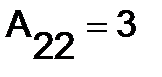 .
.
Следовательно, матрица 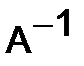 , обратная к
, обратная к  , имеет вид:
, имеет вид:
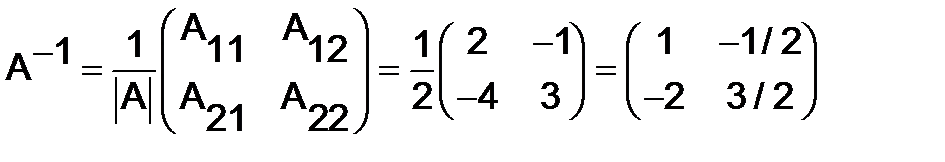 .
.
Проверим правильность полученного результата:
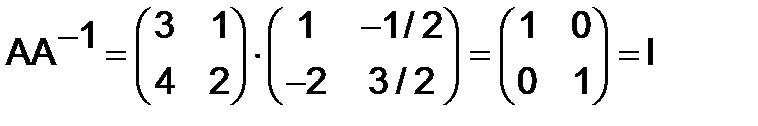 .
.
305.Найти матрицу, обратную для матрицы
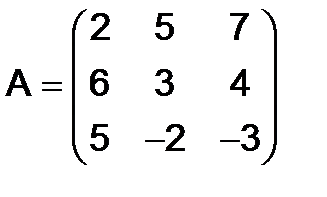 .
.
Решение. Так как 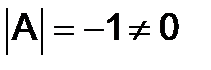 , то данная матрица является невырожденной.
, то данная матрица является невырожденной.
Вычислим алгебраические дополнения:
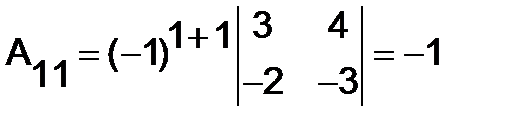 ,
, 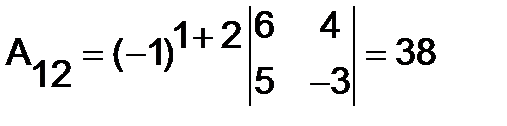 ,
,
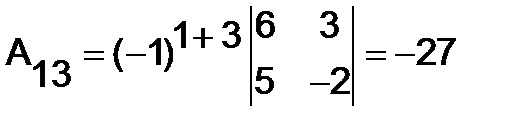
Аналогично находим 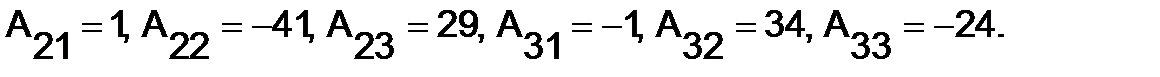
Таким образом,
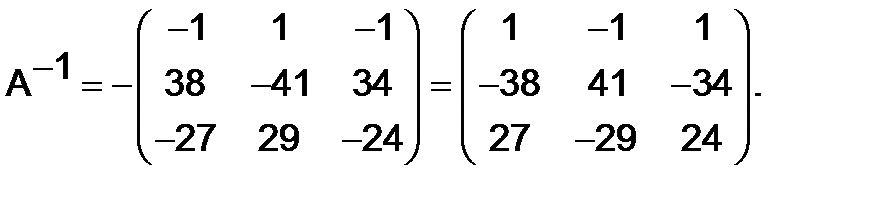
Вычислим произведение:
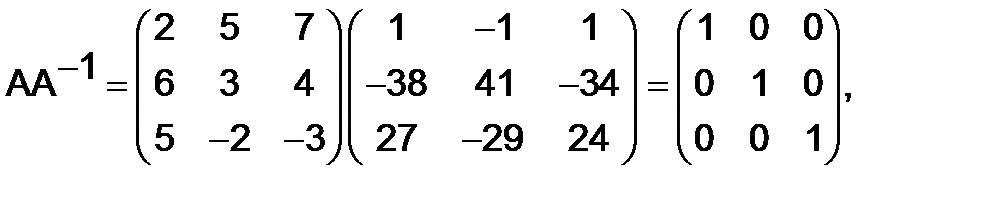
что показывает правильность полученного результата.
306.Решить матричное уравнение 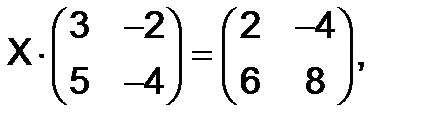 или
или 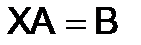 .
.
Решение. По формуле (9) имеем  . Так как
. Так как
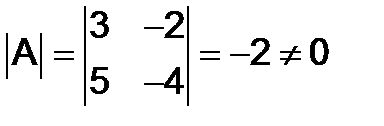 , то
, то 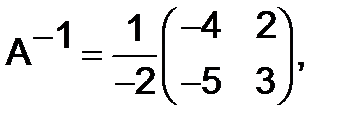 поэтому
поэтому
поэтому
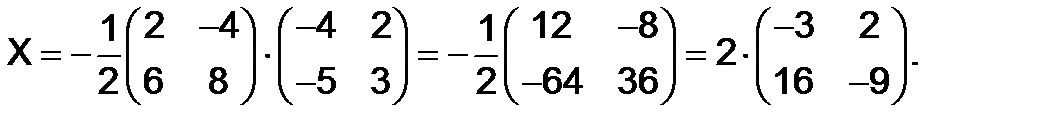
307.Показать, что матрица 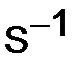 , обратная симметрической матрице
, обратная симметрической матрице
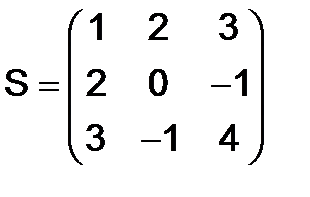 , будет тоже симметрической.
, будет тоже симметрической.
308.Найти матрицы, обратные для следующих:
а) 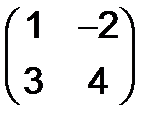 , б)
, б) 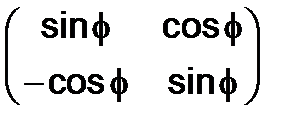 , в)
, в) 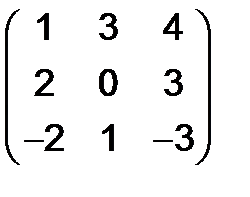 , г)
, г) 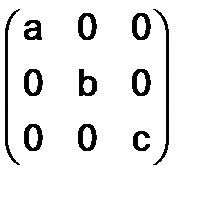 .
.
309.Решить следующие матричные уравнения:
а) 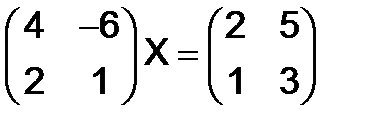 , б)
, б) 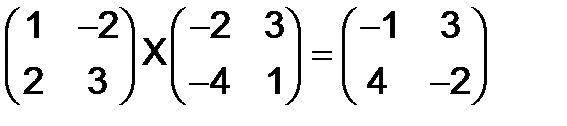 ,
,
в) 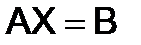 и
и 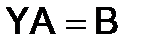 , если
, если 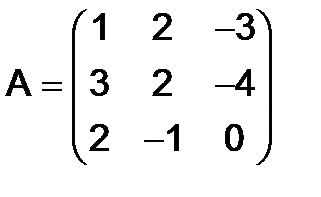 ,
, 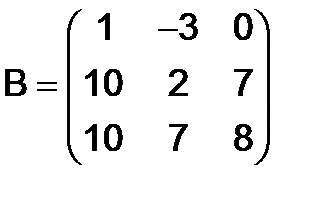 .
.
310.Показать, что если 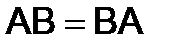 , то
, то 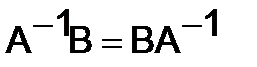 .
.
311.Как изменится обратная матрица 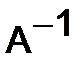 , если в матрице
, если в матрице  переставить местами две строчки?
переставить местами две строчки?
312.Показать, что если матрица  не имеет обратной , то и её произведение на любую матрицу
не имеет обратной , то и её произведение на любую матрицу 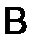 также не имеет обратной.
также не имеет обратной.
313.Две матрицы  и
и 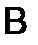 называются подобными, если они связаны равенством
называются подобными, если они связаны равенством 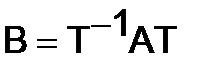 , где
, где  -некоторая невырожденная матрица .
-некоторая невырожденная матрица .
Показать, что подобные матрицы имеют одинаковые определители.
5.Прямоугольные матрицы и элементарные преобразования матриц. Прямоугольная таблица чисел, расположенных в 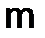 строках и
строках и 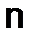 столбцах, называется прямоугольной матрицей размера
столбцах, называется прямоугольной матрицей размера 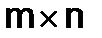 , или (
, или ( 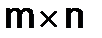 ) матрицей:
) матрицей:
 . (11)
. (11)
Элементарными преобразованиями первого рода матрицы  называются следующие действия:
называются следующие действия:
1) Умножение какой-либо строки на число 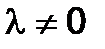 ;
;
2)Перестановка двух строк;
3)Прибавление к элементам одной строки соответственных элементов другой строки, умноженных на число 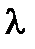 .
.
Элементарными преобразования второго рода матрицы  называются аналогичные действия со столбцами.
называются аналогичные действия со столбцами.
С помощью элементарных преобразований любую матрицу  можно привести к специальному виду:
можно привести к специальному виду:

Число r единиц, стоящих на главной диагонали, не зависит от способа приведения матрицы  к виду матрицы
к виду матрицы 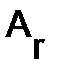 и называется рангом матрицы
и называется рангом матрицы  .
.
Матрицы, получаемые друг из друга элементарными преобразованиями называются эквивалентными и соединяются знаком ~. У эквивалентных матриц одинаковые ранги.
314.Найти ранги следующих матриц
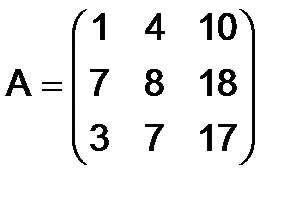 .
.
Решение.Подвергнем эту матрицу следующим элементарным преобразованиям. Ко второму столбцу прибавим первый, умноженный на (-4), а к третьему столбцу прибавим первый, умноженный на (-10), затем ко второй строке прибавим третью, умноженную на (-4). После этих преобразований полученная матрица примет вид:
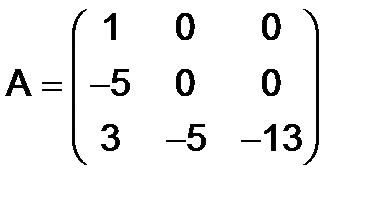 .
.
Теперь первую строку умножим на 5 и на (-3) и прибавим соответственно ко второй и третьем строка, а затем переставим местами вторую и третью строки; тогда будем иметь матрицу:
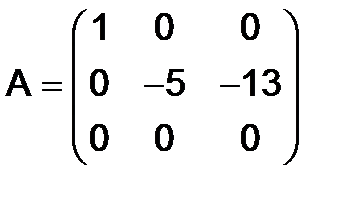 .
.
Далее, если умножить на (-1/5) и (-1/13) второй и третий столбцы, а затем вычесть из третьего столбца второй, то получим матрицу
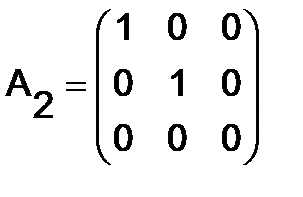 .
.
Следовательно, ранг rданной матрицы равен двум, т.е. r=2.
315.
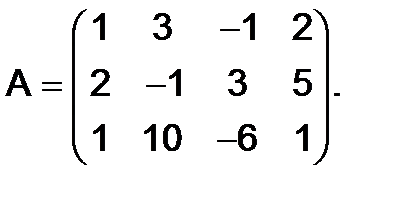
Решение. Посредством последовательных элементарных преобразований над данной матрицей получим следующую систему эквивалентных матриц :
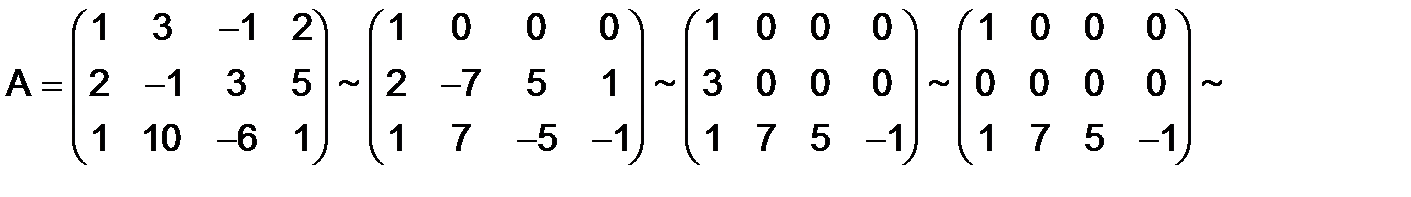
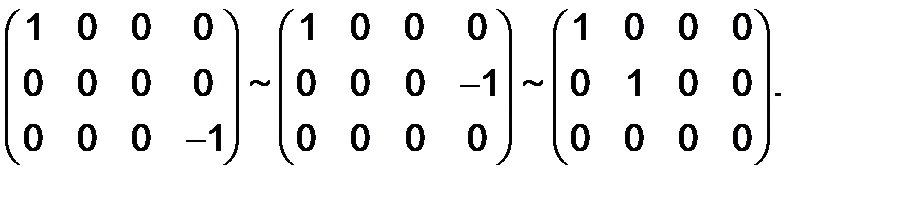
Следовательно, ранг этой матрицы равен двум.
316.Найти ранги следующих матриц:
а) 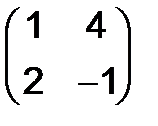 , б)
, б) 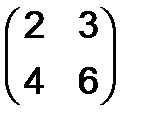 , в)
, в) 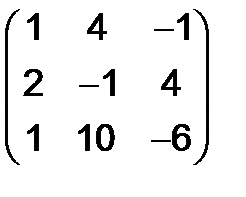 , г)
, г) 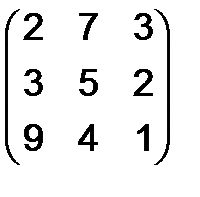 , д)
, д) 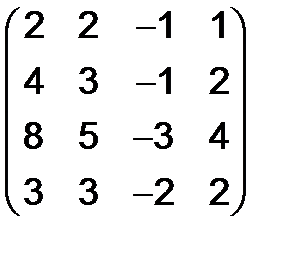 .
.
Системы линейных уравнений.
1.Формулы крамера.Пусть дана система линейных уравнений
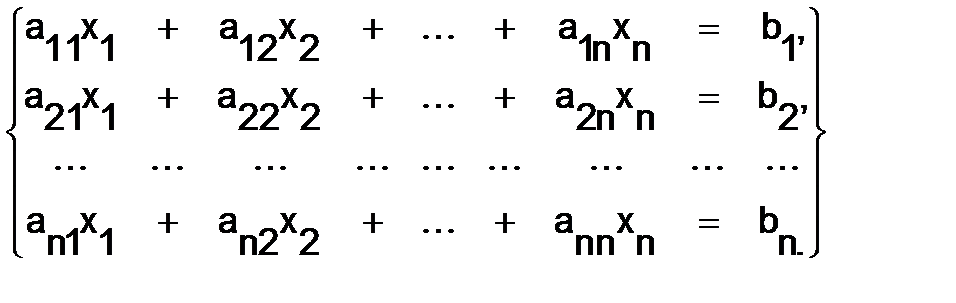 (1)
(1)
Определитель n-го порядка 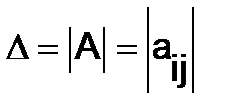 , составленный из коэффициентов при неизвестных, называется определителем системы. В зависимости от определителя системы различают следующие случаи:
, составленный из коэффициентов при неизвестных, называется определителем системы. В зависимости от определителя системы различают следующие случаи:
а)Если определитель  системы (1) отличен от нуля, то система имеет, и притом единственное, решение, которое может быть определено по формулам Крамера:
системы (1) отличен от нуля, то система имеет, и притом единственное, решение, которое может быть определено по формулам Крамера:
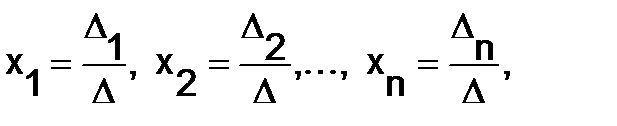 (2)
(2)
Где определитель n-го порядка 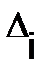 (i=1, 2,…, n) получается из
(i=1, 2,…, n) получается из  путём замены i-го столбца свободными членами
путём замены i-го столбца свободными членами 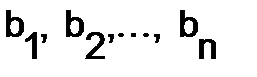 ;
;
б)Если 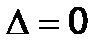 , но хотя бы один из
, но хотя бы один из 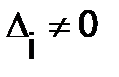 (i=1, 2,…, n), то система (1) совместна;
(i=1, 2,…, n), то система (1) совместна;
в)Если 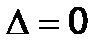 и
и 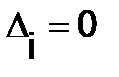 (i=1, 2,…, n), то система (1) либо несовместна, либо имеет бесчисленное множество решений [в последнем случае хотя бы одно уравнение системы (1) – следствие других ].
(i=1, 2,…, n), то система (1) либо несовместна, либо имеет бесчисленное множество решений [в последнем случае хотя бы одно уравнение системы (1) – следствие других ].
317.Решить систему
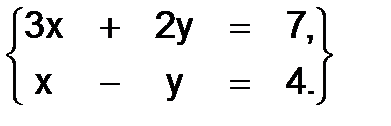
Решение. Определитель системы
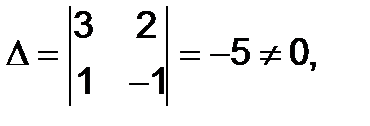
Поэтому решение её определяется по формулам Крамера:
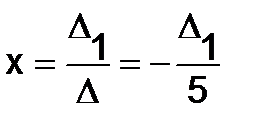 и
и 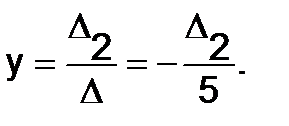
Но
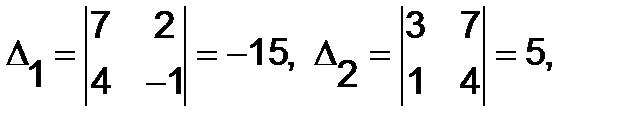
тогда
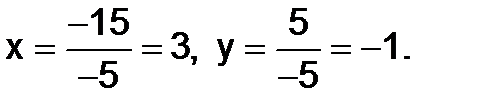
Геометрически каждое из уравнений 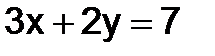 и
и 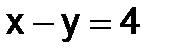 определяет прямую на плоскости x0y, и поэтому решение
определяет прямую на плоскости x0y, и поэтому решение 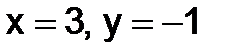 определяет точку пересечения этих прямых.
определяет точку пересечения этих прямых.
318.Исследовать систему
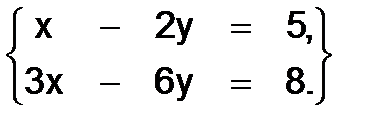
Решение. Определитель данной системы 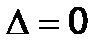 , но определить
, но определить 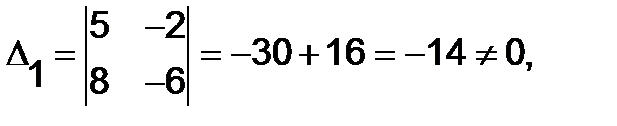 что показывает несовместность системы.
что показывает несовместность системы.
Геометрически это означает , что данные прямые не пересекаются, т.е. параллельны.
319. Решить систему
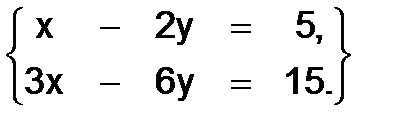 .
.
Решение. Определители 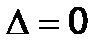
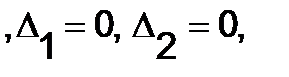 так как у них строки пропорциональны. Здесь оба уравнения системы определяют одну и ту же прямую и решением системы являются координаты любой точки этой прямой. Отсюда следует, что система имеет бесчисленное множество решений.
так как у них строки пропорциональны. Здесь оба уравнения системы определяют одну и ту же прямую и решением системы являются координаты любой точки этой прямой. Отсюда следует, что система имеет бесчисленное множество решений.
Найти все решения следующих систем:
320. 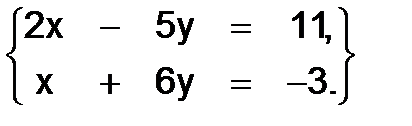 322.
322. 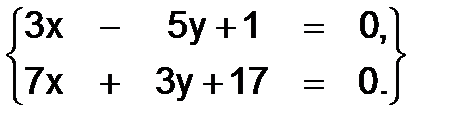
321. 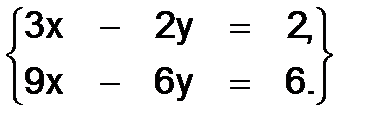 323.
323.  .
.
324.Решить систему 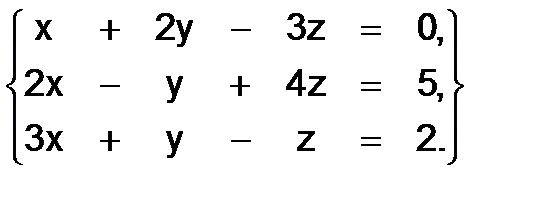
Решение. Вычисляем определители:
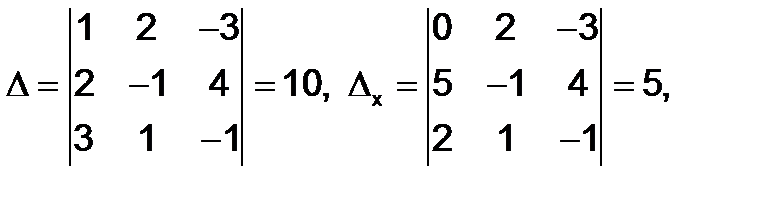
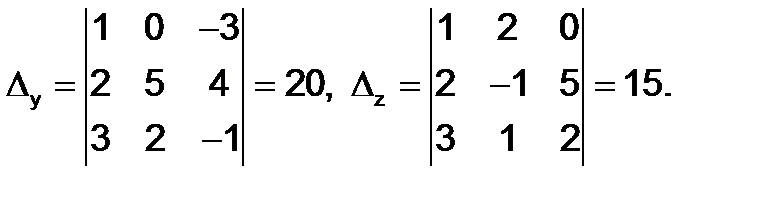
Так как 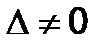 , то данная система имеет только одно решение . Находим его по формулам Крамера:
, то данная система имеет только одно решение . Находим его по формулам Крамера:
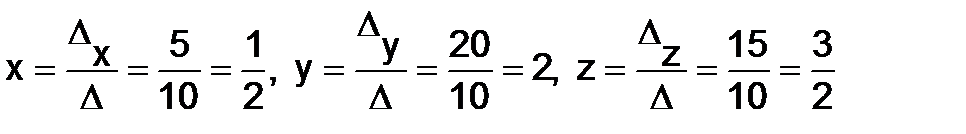
Решить следующие системы:
325. 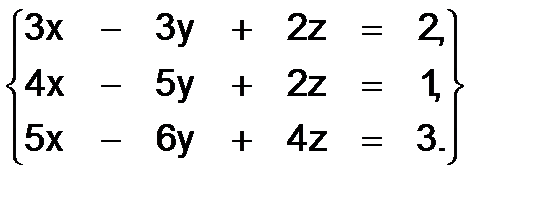 326.
326. 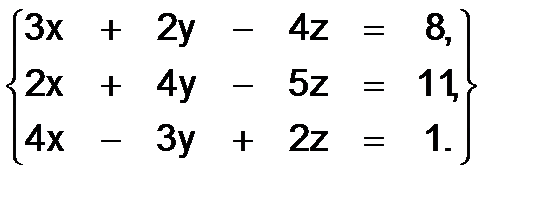
327. 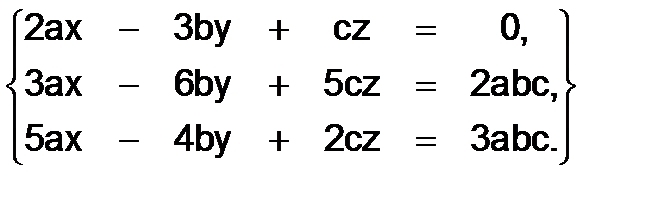
328. 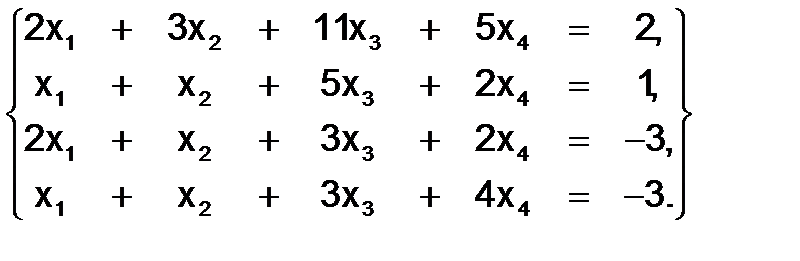
2.Решение системы с помощью обратно матрицы. Пусть дана система (1).
Её можно записать в матричной форме
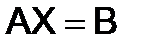 , (3)
, (3)
Где 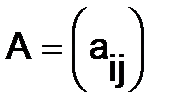 - матрица из коэффициентов при неизвестных, а
- матрица из коэффициентов при неизвестных, а 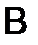 и
и  - столбцы, составленные соответственно из свободных членов и из неизвестных. Если матрица
- столбцы, составленные соответственно из свободных членов и из неизвестных. Если матрица  - невырожденная, т.е. определитель системы
- невырожденная, т.е. определитель системы 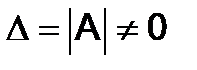 , то, умножая обе части уравнения (3) на матрицу
, то, умножая обе части уравнения (3) на матрицу 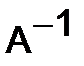 слева, получаем решение системы в матричной форме:
слева, получаем решение системы в матричной форме:
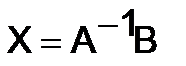
Найти решение следующих систем с помощью обратной матрицы:
329. 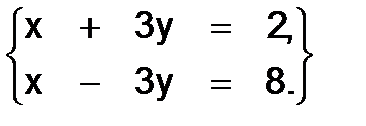
Решение. Здесь 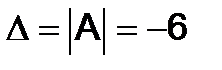 , значит матрица - невырожденная и искомое решение имеет вид (4):
, значит матрица - невырожденная и искомое решение имеет вид (4):
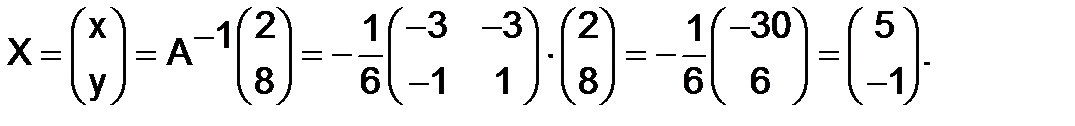
Отсюда

330. 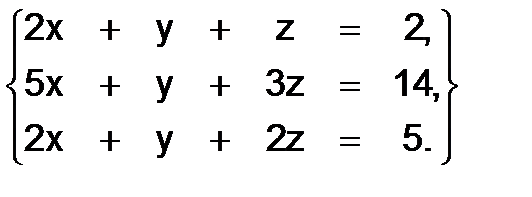
Решение. Определитель системы 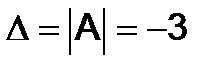 , и тогда
, и тогда
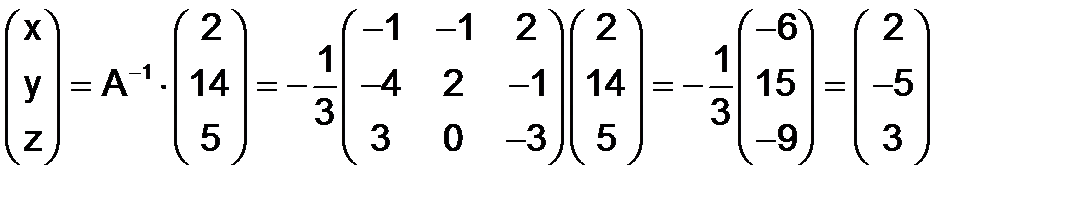
откуда и следует, что
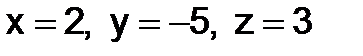
331. 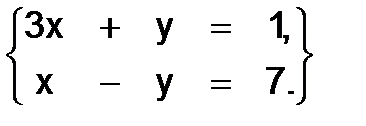
332. 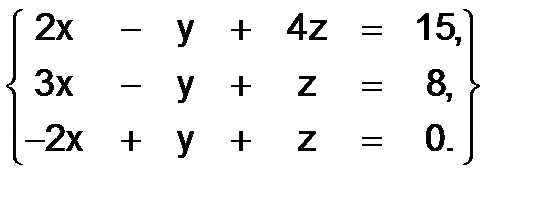
333. 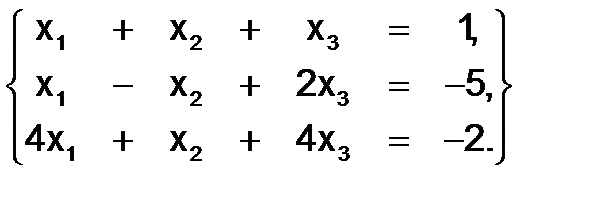
334. 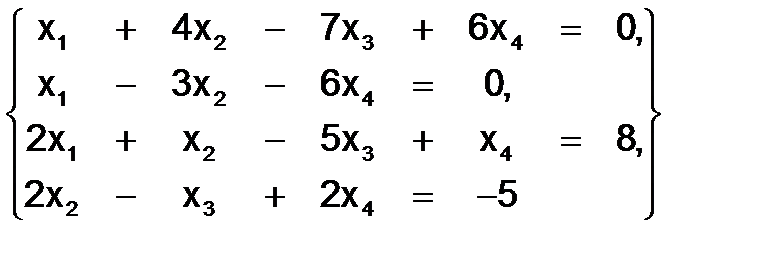
335. 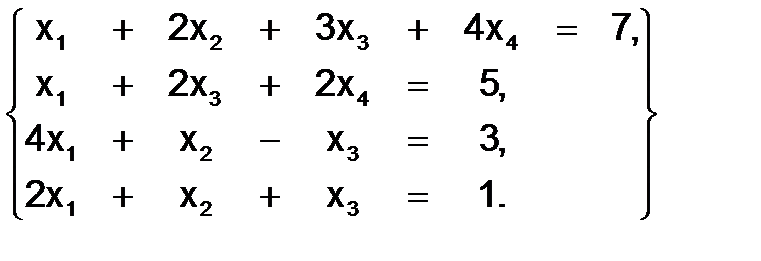
3.Однородная система линейных уравнений.Система (1) называется однородной, если все свободные члены 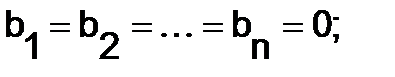 в матричной форме однородная система имеет вид
в матричной форме однородная система имеет вид
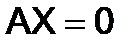 , (5)
, (5)
где 0 – нулевой столбец.
Однородная система всегда обладает тривиальным – нулевым решением:
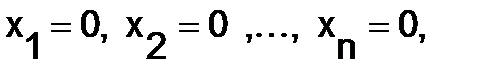
т.е всегда совместна.
Если определитель системы 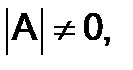 то нулевое решение будет её единственным решением. Для того, чтобы система (5) имела ненулевое решение, необходимо и достаточно, чтобы её определитель был равен нулю. Заметим, что система (5), имеющая одно ненулевое решение, имеет бесчисленное множество решений; если
то нулевое решение будет её единственным решением. Для того, чтобы система (5) имела ненулевое решение, необходимо и достаточно, чтобы её определитель был равен нулю. Заметим, что система (5), имеющая одно ненулевое решение, имеет бесчисленное множество решений; если 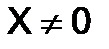 и
и 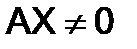 , то
, то 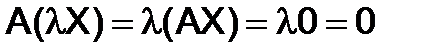 при любом
при любом 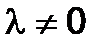 .
.
Пусть дана однородная система, например, трёх уравнений с тремя неизвестными
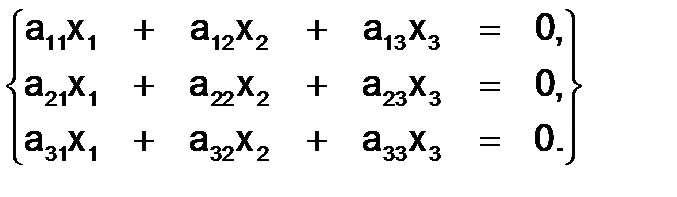 (5`)
(5`)
Здесь могут быть следующие случаи:
а) Если 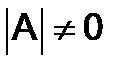 , то ненулевое решение
, то ненулевое решение 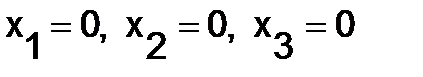 - единственное;
- единственное;
б) Если 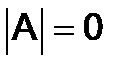 , но один из миноров второго порядка определителя отличен от нуля, тогда одно из уравнений системы является следствием двух других уравнений и данная система уравнений сводится к системе двух уравнений с тремя неизвестными, имеющей бесчисленное множество ненулевых решений ;
, но один из миноров второго порядка определителя отличен от нуля, тогда одно из уравнений системы является следствием двух других уравнений и данная система уравнений сводится к системе двух уравнений с тремя неизвестными, имеющей бесчисленное множество ненулевых решений ;
в) Если 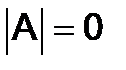 и все миноры второго порядка определителя равны нулю, то система сводится к одному уравнению с тремя неизвестными , следовательно, данная система также имеет бесчисленное множество ненулевых решений.
и все миноры второго порядка определителя равны нулю, то система сводится к одному уравнению с тремя неизвестными , следовательно, данная система также имеет бесчисленное множество ненулевых решений.
Найти все решения следующих однородных систем:
336. 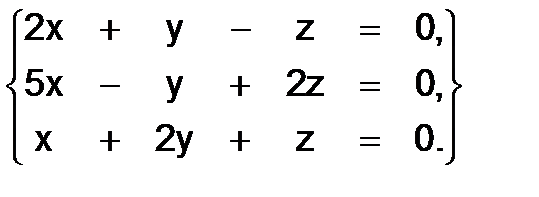
Решение. Вычислим определитель системы:
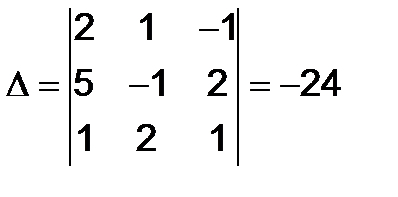 .
.
Поскольку 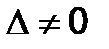 , то данная система имеет только одно ненулевое решение:
, то данная система имеет только одно ненулевое решение:
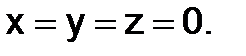
337. 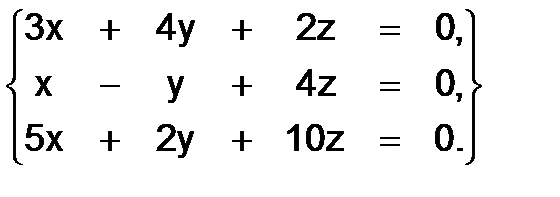
Решение. Определитель данной системы
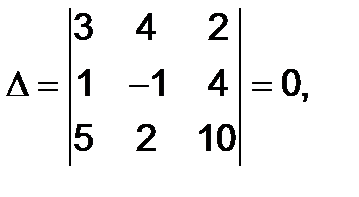
Поэтому система имеет ненулевые решения. Замечаем, что миноры, содержащиеся в первых двух строчках, отличны от нуля, например,
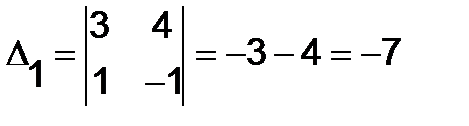
Здесь для получения третьего уравнения надо прибавить к первому удвоенное второе (проверить!), т.е. третье уравнение- следствие первых двух, и система сводится к двум уравнениям:
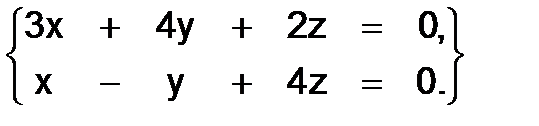
Задавая произвольно одно из них, например Z, из этих двух уравнений найдём значения X и Y. Полагая в данном случае Z=h, получим
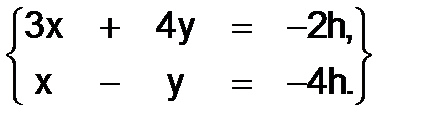 ,
,
откуда
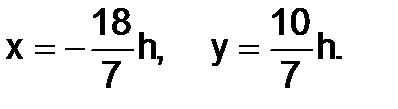
Следовательно, решение системы можно записать в виде:
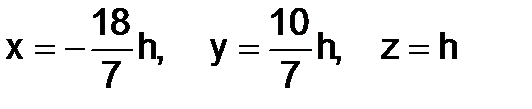 ,
,
где h – произвольно число.
338. 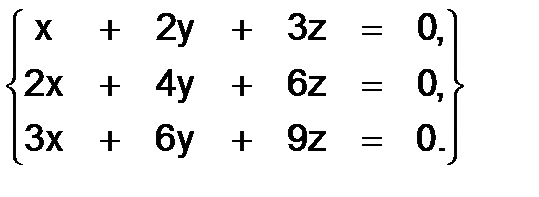
Решение. Нетрудно подсчитать, что здесь сам определить и все его миноры равны нулю. Это значит, что в данной системе только одно независимое уравнение, а остальные два ему пропорциональны. Находя, например, из первого уравнения 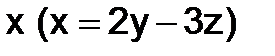 при произвольных
при произвольных 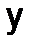 и
и 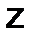 , получим решение данной системы. Общий вид решения можно записать так:
, получим решение данной системы. Общий вид решения можно записать так:
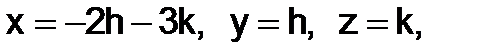
где h и k – произвольные числа.
