Механизма поперечно-строгального станка

Выполнил студент группы 23202

Фатхуллин И.И.

Проверил преподаватель

Гавариев Р.В.

Набережные Челны

2016 г.

THE MINISTRY OF EDUCATION AND SCIENCE OF

THE RUSSIAN FEDERATION STATE EDUCATIONAL

INSTITUTION OF HIGHER

EDUCATION

Naberezhnye Chelny branch of Kazan national research

Technical University named after A.N. Tupolev

The Department "Design and technology of machine-building production"

Course project in the discipline

"Theory of mechanisms and machines"

Version 3.2

Completed student group 23202

Fatkhullin I.I.

Checked teacher

Gavariev R.W.

Naberezhnye Chelny

2016 г.

Рычажный механизм

Кинематический анализ и силовой расчёт:

механизма поперечно-строгального станка

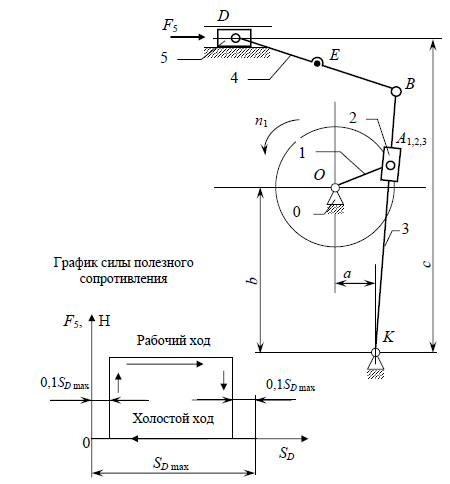
Исходные данные:

Параметры	Значения
a, мм
b, мм
c, мм
lOA, мм
lKB, мм
lBD, мм
lBE, мм
n1, об/мин
F1, H

· звено0 - стойка;

· звено 1 - кривошип;

· звено 2 - камень кулисы;

· звено 3 -кулиса;

· звено 4 -шатун;

· звено 5 - ползун;

1) Механизм образован:

к ведущему звену OA и стойке - точка K присоединена группа Ассура второго класса третьего вида, состоящая из звеньев 2 и 3, а к этой группе и стойке присоединена группа второго класса второго вида, состоящая из звеньев 4 и 5, следовательно, заданный механизм следует отнести ко второму классу.

Начальных механизмов – 1.

Структурных групп (групп Ассура) – 3, соединение групп – последовательное.

Механизм второго класса.

Формула построения в развернутом виде:

-В_0,1-[П_2,3-В_3,0­-В_3,0]-[В_3,4-В_4,5-П_5,0]

Степень подвижности:

ω=3n-2p₅-p₄=3*5-2*7-0=1,

Это означает, что для придания определенности движения звеньям механизма достаточно задать движение одному звену.

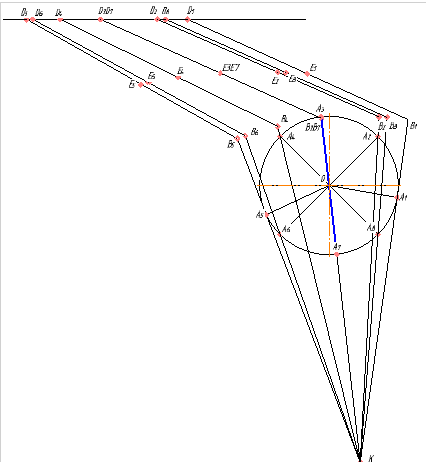
Рис. 1 Траектория движения всех характерных точек

2) Строим план положения механизма:

Длину отрезка OA выбираем равной 50 мм, поэтому масштаб схемы будет

μ_l=l_OA/OA=0,002 мм/м,

Длины остальных отрезков на чертеже:

KB=l_KB/ μ_l =250 мм.

BD=l_BD/ μ_l =175 мм.

BE=l_BE/ μ_l=80 мм.

3) Строим план скоростей механизма:

1. Определяем скорость ведущей точки механизма, т.е. точки звена, закон движения которого задан. В нашем случае это точка Aзвена 1,

V_A=ω₁*L_OA,

где

ω₁=(π*n)/30=(3,14*190)/30=19,89 1/c

V­_A­=19,89 *0,05=0,99м/с,

Примем масштаб построения плана скоростей μ_ν=ω_1*μ_l=19,89 1/c *0,002 мм/м=0.0397 ,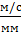

вектор скорости точки A:

V=V_A/μ_ν=0,99/0,01988=50 мм.

Начинаем построение плана скоростей механизма с группы, состоящей из звеньев 2 и 3, так как она непосредственно присоединена к ведущему звену и стойке. Построение ведем по следующим уравнениям:

V_A3=V_A+V_A3A,

V_A3=V_K+V_A3K,

где V_A3 – скорость точки A₃звена, которая лежит под точкой A;V_A – скорость точки A, по модулю равна V_A=0,99 м/с и направленная перпендикулярно OAв соответствии с направлением угловой скорости ω₁; V_A3A– скорость точки A₃относительное A, направленная параллельно линии AK; V_K – скорость точки K, равна нулю; V_A3K – скорость точки A во вращении звена 3 относительно точки K, по модулю равна V_A3K=V_A=ω₃*L_A3Kи направленная перпендикулярно AK.

Строим решение первого векторного уравнения, указанного выше. От полюса p плана откладываем отрезок pb, изображающий скорость V_A точки A.

Длину этого отрезка принимаем равной pb=OA=50 мм., т.е. план строим в масштабе кривошипа. Через точку aпроводим направление скорости V_A3A – линию параллельную KA₃. Переходим к построению решения второго векторного уравнения, указанного выше. Надо отложить вектор скорости токи K, но так как модуль его равен нулю, то конец его с помещаем в полюс плана pи из точки pпроводим направление скорости V_KA3 – линию, перпендикулярную KB. Пересечение ее с ранее проведенной линией, параллельной KB, дает конец вектора скорости V_A3 – точку a₃.Тогда b – конец вектора скорости точки B – находим правилу подобия из соотношения:

,

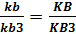kb=kb_­3 ₌

Переходим к построению плана скоростей группы 4 и 5.

Этот план строим по уравнениям:

V_D=V_B+ V_DB,

где V_D – скорость точки D, V_B - скорость точки B;V_BD – скорость точки Dво вращении звена 4 относительно точки B, по модулю равная V_DB=ω_4*l_BDи направленная перпендикулярно линии DB(пока нам не известна).

Построение сводится к проведению через точку bлинии, перпендикулярной BD, т.е. направлению скорости V_DB, и проведению через точку p(согласно второму уравнению) линии, параллельный xx. Точка dпересечения этих линий есть конец вектора скорости V_DточкиD. Помещаем в полюс точки k, oи на этом заканчиваем построение плана скоростей механизма.

Результаты по определению линейных скоростей и угловых скоростей звеньев сводим в Таблицу 1.

4) Строим план ускорений механизма:

a_A3= a_A+ a^k_A3A+ a^r_A3A, a_A3= a_K+ aⁿ_KA3+ a^t_A3A

Строим план ускорений группы 2, 3. Построение ведем по следящим двум векторным уравнениям:

гдеa_A3- ускорение точки A₃, которая принадлежит звену 3 и совместилась с точкой A звена 1; a_A - нормальное (оно же полное) ускорение точи __, по модулю равноеa_A = ω²₁*l_AB и направлено параллельноAOот точки A к точке O; a^k_A3A - ускорение Кориолиса в движении точки A₃ относительно звена 2, по модулю равное:

a^k_A3A= 2ω₂*V_A3A =2(V_A3K* V_A3A)/ l_AK

(так как ω₂ = ω₃иω₂ = V_A3K/ l_AK)и имеющие направлении вектора относительной скорости V_A3A,повернутого на 90⁰ в направлении угловой скорости ω₂ переносного движения (движения звена 2); a^r_A3A–относительное (релятивное) ускорение точки A₃относительно точки A, направленное параллельно линии KA; a_K –ускорение точки K(оно равно нулю);aⁿ_KA3 - нормальное ускорение точи __ во вращении звена 3 относительно точки K, по модулю равное:

aⁿ_KA3 = V²_A3K/ l_A3A

и направленное параллельно линии KA₃ от точки A₃ к точке K; a^t_A3A - касательное ускорение точки A₃ в том же движении звена 3, по модулю равное a^t_A3A = ε₃*l_A3K (нам пока не известно) и направленное перпендикулярно KA₃.

Строим решение первого векторного уравнения, указанного выше. Задаемся отрезком(πb) = (OA) = 50 мм., который изображает в плане ускорение a_A, (так как (πb) = (OA), то план строится в масштабе кривошипа).

Масштаб плана ускорений равен:

µ_a = a_A/(πa) = (ω²₁*(AB)* µ_l)/ (πa) = ω²₁* µ_l

Масштаб плана аналогов ускорений равен:

µ_φa = µ_a/ω²₁= µ_l

Выбранный отрезок (πa) откладываем от полюса плана (π), далее к нему прибавляем отрезок (ak) - вектор кориолисова ускорения – его длину находим по формуле:

(ak) = a^k_A3A/ µ_a = (2V_A3K* V_A3A) / (l_A3K* µ_a) = (2(a₃k)*(aa₃)* µ²_v )/ ((A₃K)*µ_l* µ_a))

отрезки (a₃k)и(aa₃)взяты из плана скоростей, а отрезок (A₃K) - из плана положений).

Через точку k проводим, направление ускорения a^r_A3A - линию, параллельную KA.

Переходим к построению второго векторного уравнения. Точку k совмещаем с точкой π, так как a_K, от точки π откладываем отрезок(πn_A3K), изображающий нормальное ускорениеaⁿ_A3K, его длина равна:

(πn_A3K) = V²_A3K/ l_A3K µ_a=((pa₃)² µ²_v)/((A₃K) µ_l µ_a)

далее через точкуn_A3K проводим направление ускорения a^t_A3A - линию, перпендикулярную KA, до пересечения с ранее проведенной через точку k линией, параллельной KA.

Точка пересечения a₃ представляет собой конец вектора ускорения a_A3. Конец вектора ускорения центра B (точку b) найдем по правилу подобия из соотношения:

(πd) = ((πa₃)*KB)/A₃K

Переходим к построению плана ускорений группы 4, 5 по уравнению:

a_D= a_B+aⁿ_DB+ a^t_DB

где a_D - ускорение точки D; a_B - ускорение точки B (оно определяется по ранее построенному отрезку (πd):

aⁿ_DB= V²_DB/l_DB- нормальное ускорение точки D во вращении звена 4 относительно точки B(оно направлено параллельно линии DB от точки D к точке B);

a^t_DB = ε₄*l_DB- касательное ускорение той же точки в том же движении звена 4 (оно направлено перпендикулярно линии DB);

В соответствии с первым векторным уравнением от точки bоткладываем отрезок (bn_DB), изображающий нормальное ускорение a^t_DB. Его длина равна:

bn_DB=V²_DB/l_DBμ_a

Далее через точку n_DB проводим направление ускорения a^t_DB (линию, перпендикулярную DB) и переходим построениям, соответствующим второму векторному уравнению, указанному выше.

Подставляя, полученные из кинематического исследования, значения в вышеуказанные формулы находим: линейные скорости и ускорение точек, а также угловые скорости и ускорения звеньев (Таблица 1):

Таблицы 1/2/3

Положение механизма	Отрезки на плане скоростей (мм.)	Линейные скорости точек (м/с)	Угловые скорости звеньев (1/с)
pva	pva3	pva2/a3	pvb	pvbd	pvbe	pvd	VA	VA3	VKA3	VB	VBD	VBE	VD	ω1	ω2	ω3	ω4	ω5
		1.782	33.39	2.28	0.35	0.16	2.40	1.99	0.07	1.33	0.09	0.01	0.01	0.10	19.89	1.4175	0.3627	0.0786	0.5457
		37.23	49.968	43.00	2.56	1.17	43.96	1.99	1.48	1.99	1.71	0.10	0.05	1.75	19.89	29.6152	6.8407	0.5816	9.9920
		42.773	25.893	55.35	14.72	6.73	47.25	1.99	1.70	1.03	2.20	0.59	0.27	1.88	19.89	34.0245	8.8058	3.3464	10.7393
		3.693	49.863	4.78	1.95	0.89	3.51	1.99	0.15	1.98	0.19	0.08	0.04	0.14	19.89	2.9377	0.7605	0.4425	0.7975
		45.076	21.634	64.71	69.63	31.83	54.93	1.99	1.79	0.86	2.57	2.77	1.27	2.18	19.89	35.8565	10.2949	15.8241	12.4838
			32.495	49.18	53.61	24.51	17.85	1.99	1.51	1.29	1.96	2.13	0.97	0.71	19.89	30.2277	7.8242	12.1838	4.0562

Примечание: под №1 –положение механизма при рабочем ходе; под №5 – положение механизма – одно из крайних (мёртвых).

Положение механизма	Отрезки на плане ускорений (мм.)	Линейные ускорения точек (м/с2)
pva	pa a3	pa b	pa bd	pa be	pa d	Va	Va3	Vb	Vbd	Vbe	Vd
		50.584	65.466	9.950	4.549	68.944	39.55	40.01	51.8	7.9	3.6	54.5
		18.546	19.671	6.230	2.848	22.384	39.55	14.67	15.6	4.9	2.3	17.7
		35.836	36.965	18.689	8.544	23.890	39.55	28.34	29.2	14.8	6.8	18.9
		46.101	60.249	24.414	11.161	44.392	39.55	36.46	47.7	19.3	8.8	35.1
		30.428	43.590	90.375	41.314	133.868	39.55	24.07	34.5	71.5	32.7	105.9
		53.671	81.249	22.151	10.126	59.920	39.55	42.45	64.3	17.5	8.0	47.4

Положение механизма	arA3K, м/с2	arDB, м/с2	arA, м/с2	Ɛ3,1/с2	Ɛ4, 1/с2	Ɛ1, 1/с2
	40.01	7.87	1.41	207.1	45.0	28.2
	13.91	2.68	24.79	59.0	15.3	495.8
	27.71	14.74	39.80	114.3	84.2	796.0
	37.92	19.31	2.97	198.2	110.3	59.5
	22.23	68.04	24.12	127.4	388.8	482.3
	41.88	11.76	32.62	253.6	67.2	652.4

5) Силовой расчет механизма:

Определим силы, действующие на звенья механизма. При определении сил, кроме заданных сил (моментов) производственных сопротивлений, учтём силы тяжести, силы и моменты инерции звеньев.

Силами трения в кинематических парах можно пренебречь.

Исходные данные

Ускорения центра тяжести звеньев

а_S1=19.77

а_S3=29.24

а_S4=23.94

а_S5=1.88

Массы и моменты инерции звеньев не заданы, определим на основании эмпирических зависимостей:

m­_i= k*l_i ,

гдеk – масса одного погонного метра звена:

l_i– длина звеньев i,м

k = 8 … 12 кг/м – для кривошипа;

k = 10 … 20 кг/м – для кулисы;

k = 20 … 30 кг/м – для шатунов;

Масса (звено 1) кривошипа–m₁=10 кг.

Масса (звено 3) кулиса–m₃=15 кг.;

Масса (звено 4) шатун – m₄=25 кг.;

Рабочим звеном механизма является звено 5, к которому приложено полезное (производственное) сопротивление М₅, определяющееся из графика для данного положения механизма. Помимо заданного момента полезного сопротивления (или заданных сил), учтем силы тяжести, силы и моменты инерции звеньев.

Примем масштабный

μ_F=0,10 H/мм

Найдем значения:

сил тяжести каждого из звеньев:

F_G1=g*m₁=9,8*10=98

F_G3=g*m₃=9,8*15=147

F_G4=g*m₄=9,8*25=245

F_G5=g*m₅=9,8*5.22=245

главных векторов сил инерции:

F_i1=m₁*a_S1=10*19,77 м/с²=98

F_i3=m₃*a_S3=20*29,74 м/с²=196

F_i4=m₄*a_S4=25* 23,94 м/с²=245

F_i5=m₅*a_S5=5.22* 23,94 м/с²=245, при m=(30…60)S, где S – ход резца от мертвого до мертвого значения.

моментов инерций:

Jsi=mi*l²i/3 – для кривошипа;

Jsi=mi*l²i/13 – для всех остальных звеньев рычажного типа;

li – длина звена;

Ji1=0,08 кг/м²

Ji3=0,078 кг/м²

Ji4=0,025 кг/м²

главных моментов сил инерции:

M_i= Ji* Ɛ1

где:

Ɛ1=796 1/с²

Ɛ3=114 1/с²

Ɛ4=84 1/с²

M_i1=63,8

M_i3=8,9

M_i4=2,1

Силовой расчёт группы 4-5

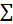M_D=F^r_R43*l_BD+F_G4*h_G4+F_i4*h_i4-M_i4=0

где плечи сил (определяются по чертежу с учётом масштаба μl)

h_G4=85,249=0.17

h_i4=94,79=0.19

Из уравнения равновесия находим неизвестную реакцию:

F^r_R43= (F_G4*h_G4+F_i4*h_i4-M_i4)/ l_BD=398H

Fⁿ_R43+F^r_R43+F_G4+F_i4+ F_G5+ F_i4+ F_5c+F₅₀=968 H

Силовой расчёт группы 2-3

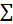M_K=F^r_R32*l_AK+F_G3*h_G3+F_i4*h_i3-M_i3=0

где плечи сил (определяются по чертежу с учётом масштаба μl=0,002 м/мм)

h_G4=29,84*0,002=0,059

h_i4=122,2*0,002=0,24

Из уравнения равновесия находим неизвестную реакцию:

F^r_R32= (F_G3*h_G3+F_i3*h_i3-M_i3)/ l_BD=442H

F_R43+F_R32+F_G3+F_i3+ F₃₀=869 H

Силовой расчёт начального

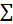M_O=-F_ур.*l_AO+ F_G1*h_G1+F₂₁*h_F21,

где плечи сил (определяются по чертежу с учётом масштаба μl)

h_G4=17,68*0,002=0,085

h_F21=42,76*0,002=0,35

F_ур.=(F_G1*h_G1+F₂₁*h_F21)/l_AO=198,8