Лементы специальной теории относительности

Длина l тела, движущегося со скоростью υ относительно некоторой системы отсчета, связана с длиной l₀ тела, неподвижного в этой системе, соотношением

,

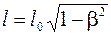где β=υ/с, с – скорость распространения света.

Промежуток времени Δτ в системе, движущейся со скоростью υ по отношению к наблюдателю, связан с промежутком времени Δτ₀ в неподвижной для наблюдателя системе соотношением

.

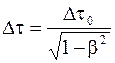Зависимость массы m тела от скорости υ его движения дается уравнением

,

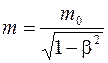где m₀ – масса покоя этого тела.

Зависимость кинетической энергии тела от скорости υ его движения дается уравнением

.

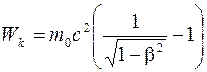Изменение массы системы на Δm соответствует изменению энергии системы на

ΔW=c² Δm.

Релятивистский закон сложения скоростей для тела, движущегося вдоль оси OX, имеет вид

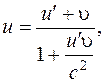
где υ – скорость движущейся системы отсчета K′, u′ – скорость относительно системы K′, u – скорость относительно неподвижной.

4. 1. Две нестабильные частицы движутся в системе отсчета К в одном направлении вдоль одной прямой с одинаковой скоростью υ = 0,6 с. Расстояние между частицами в системе К равно 64 м. Обе частицы распались одновременно в системе К', которая связана с ними. Определить промежуток времени между распадом частиц в системе К.

4. 2. Определить, во сколько раз увеличивается время жизни нестабильной частицы (по часам неподвижного наблюдателя), если она начинает двигаться со скоростью, равной 0,9 с.

4. 3. Собственное время жизни частицы отличается на 1 % от времени жизни по неподвижным часам. Определить β = υ/c.

4. 4. Космический корабль движется со скоростью υ = 0,8 с по направлению к Земле. Определить расстояние, пройденное им в системе отсчета, связанной с Землей (системе К), за t_o = 0,5 с, отсчитанное по часам в космическом корабле (системе К').

4. 5. Мюоны, рождаясь в верхних слоях атмосферы, при скорости υ = 0,995 с пролетают до распада l = 6 км. Определить: 1) собственную длину пути, пройденную ими до распада; 2) время жизни мюона для наблюдателя на Земле; 3) собственное время жизни мюона.

4. 6. Определить относительную скорость движения, при которой релятивистское сокращение линейных размеров тела составляет 10%.

4. 7. В системе К' покоится стержень (собственная длина l₀ = 1,5 м), ориентированный под углом θ' = 30° к оси Ох'. Система К' движется относительно системы К со скоростью υ = 0,6 с. Определить в системе К: 1) длину стержня 1; 2) соответствующий угол .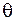

4. 8. Определить собственную длину стержня, если в лабораторной системе его скорость υ = 0,6 с, длина l = 1,5 м и угол между ним и направлением движения 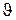=30°.

4. 9. Ионизованный атом, вылетев из ускорителя со скоростью 0,8 с, испустил фотон в направлении своего движения. Определить скорость фотона относительно ускорителя.

4. 10. Две ракеты движутся навстречу друг другу относительно неподвижного наблюдателя с одинаковой скоростью, равной 0,5 с. Определить скорость сближения ракет, исходя из закона сложения скоростей: 1) в классической механике; 2) в специальной теории относительности.

4. 11. Частица движется со скоростью υ = 0,8 с. Определить отношение массы релятивистской частицы к ее массе покоя.

4. 12. Определить на сколько процентов масса релятивистской элементарной частицы, вылетающей из ускорителя со скоростью υ = 0,75 с, больше ее массы покоя.

4. 13. Определить скорость движения релятивистской частицы, если ее масса в два раза больше массы покоя.

4. 14. Определить релятивистский импульс протона, если скорость его движения υ = 0,8с.

4. 15. Определить скорость, при которой релятивистский импульс частицы превышает ее ньютоновский импульс в n = 3 раза.

4. 16. Полная энергия релятивистской частицы в 8 раз превышает ее энергию покоя. Определить скорость этой частицы.

4. 17. Кинетическая энергия частицы оказалась равной ее t энергии покоя. Определить скорость частицы.

4. 18. Определить релятивистский импульс p и кинетическую энергию Т протона, движущегося со скоростью υ = 0,75 с.

4. 19. Определить кинетическую энергию электрона, если масса движущегося электрона втрое больше его массы покоя. Ответ выразить в электронвольтах.

4. 20. Определить работу, которую необходимо совершить, чтобы увеличить скорость частицы с массой покоя m_o от 0,5 с до 0,7 с.

4. 21. Определить релятивистский импульс электрона, кинетическая энергия которого Т = 1 ГэВ.