Определения, элементы, способы задания

Глава 3. Графы

Основные понятия

Определения, элементы, способы задания

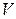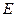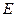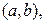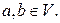Пусть дано конечное множество (его мы будем называть множеством вершин) и множество (множество рёбер), причём элементами множества являются неупорядоченные пары где Пара 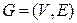называется графом. Графы изображаются следующим образом: вершина 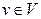– точкой, ребро 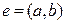– линией, соединяющей точк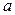и и Часто рёбра изображаются в виде отрезков прямых.

Если 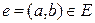– ребро, то вершины 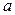и 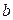называются смежными: говорят, что вершины 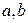инцидентны ребру 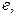а ребро 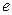инцидентно каждой из вершин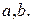

Введём в рассмотрение некоторые часто встречающиеся (стандартные) графы (см. рис. 3.1).

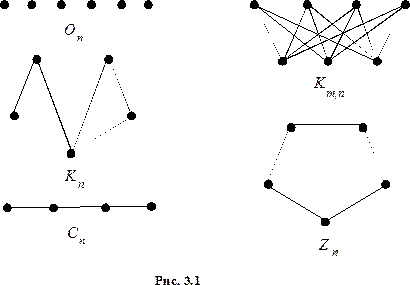
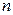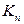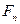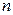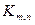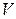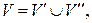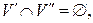
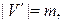
– граф с вершинами, у которого нет ни одного ребра. (или ) – полный граф, т.е. граф с вершинами, у которого любые две вершины соединены ребром. – полный двудольный граф: его множество вершин представимо в виде где 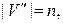а множество рёбер совпадает с множеством пар 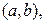где 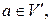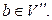Далее, 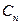– цепь, 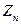–цикл с 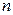вершинами. На рисунке 1 изображены графы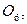

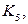
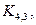
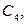
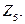
Замечание. Классическое (приведённое выше) определение графа предполагает, что графы конечные, неориентированные, без кратных рёбер и петель. Однако, в ряде случаев от этих требований можно отказаться и рассматривать более широкие классы объектов, к числу которых относятся:

1) графы с кратными рёбрами (см. рис. 3.2а);

2) графы с петлями (см. рис. 3.2б):

3) бесконечные графы.

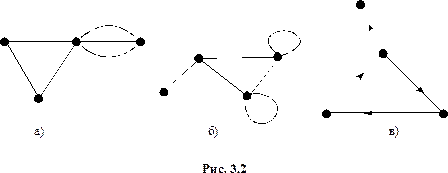
Кроме того, важное место в теории графов занимают ориентированные графы, т.е. графы, рёбра которых являются упорядоченными парами вершин (см. рис. 3.2в).

Обозначим через 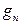количество графов с заданным множеством 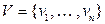вершин. Каждое ребро – это пара вершин. Всего 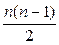пар вершин. Каждая пара вершин может либо соединяться ребром, либо не соединяться – имеется 2 возможности. Значит, 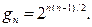Это число растёт очень быстро с ростом числа 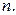Например,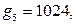

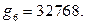
Упражнение 3.1. Изобразить графы

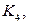
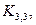
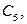
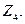
Решение этой задачи представлено на рисунке 3.3.

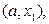
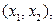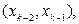
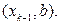Путь в графе – это множество рёбер …, Простой путь – путь, в котором все вершины 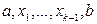различны. Замкнутый путь (или цикл) – путь, в котором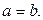

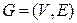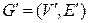Два графа и называются изоморфными (обозначается: 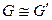), если существует взаимно однозначное отображение 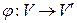такое, что

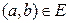
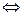
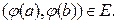(1)

Отображение 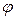называется изоморфизмом.

Например, имеют место изоморфизмы: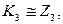

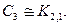
Изоморфные графы с точки зрения теории графов являются одинаковыми, у них одни и те же свойства, выражаемые в терминах теории графов – например, одинаковое количество вершин, рёбер, простых циклов, вершин, из которых исходит ровно 2 ребра и т.д. Конечно, те свойства, которые не выражаются в теоретико-графовых терминах, у них могут быть разные (образно говоря, у одного из изоморфных графов вершины могут быть красными, а у другого зелёными).

Возникает естественный вопрос: как установить, изоморфны два данных графа или нет. Ответить на этот вопрос не всегда просто. Для доказательства изоморфности графов и обычно указывают отображение 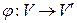(каким-то образом до него догадавшись), а затем проверяют выполнение условия (1). Для доказательства неизоморфности можно поступить так: найти какое-нибудь свойство, которым обладает один из графов и не обладает другой – но это свойство должно формулироваться в теоретико-графовых терминах без привлечения посторонних понятий. Другой метод установления изоморфности или неизоморфности графов – с помощью матрицы смежности или инцидентности – будет рассмотрен позже.

Упражнение 3.2. Выяснить, какие из графов, изображённых на рисунке 3.4, изоморфны друг другу.

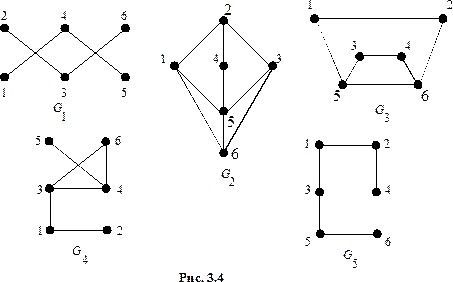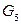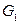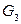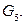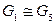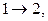
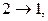
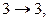
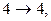
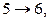
Решение. Графы изоморфны друг другу: действительно, графы и можно “перерисовать” так, что получится граф Можно привести и формальное доказательство: например, изоморфизм определяется отображением 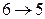(это отображение взаимно однозначно и удовлетворяет условию (1)). Граф 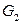не изоморфен ни одному из остальных, так как у него 10 рёбер, а у остальных – по 7. Граф 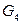также не изоморфен ни одному из остальных, так как у него есть вершина, инцидентная только одному ребру (вершина 5), а другие графы таких вершин не имеют.

Назовём степенью вершины 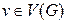(обозначается: 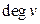) количество рёбер, инцидентных этой вершине. Вершина 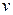называется изолированной, если 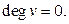Вершина 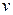называется висячей, если 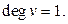Для графа пусть Р – количество его рёбер, В – количество вершин, К – количество компонент связности.

Упражнение 3.3. Найти количество вершин и рёбер графов 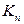и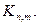

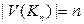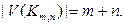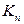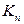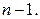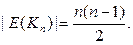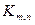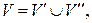
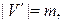
Решение. Очевидно, и Найдём количество рёбер. Так как каждая вершина графа соединена рёбрами со всеми остальными, то степень каждой вершины графа равна Если мы умножить количество вершин на степень одной вершины, то получим удвоенное количество рёбер (действительно, каждое ребро инцидентно ровно двум вершинам, а значит, будет подсчитано дважды). Таким образом, У полного двудольного графа имеем: 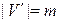и из каждой вершины 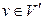исходит ровно 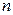рёбер. Это будут все рёбра графа и каждое из рёбер подсчитывается один раз. Следовательно,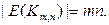

Замечание. Среди всех графов с 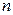вершинами полный граф 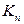имеет наибольшее количество рёбер, поэтому в любом графе с 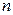вершинами не более 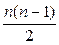рёбер:

(2)

Упражнение 3.4.Определить, сколько всего неизоморфных графов, имеющих 12 вершин и 64 ребра.

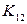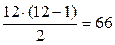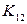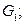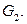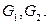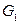Решение. Пусть – граф с 12 вершинами и 64 рёбрами. Полный граф имеет рёбер. Следовательно, граф получается из графа удалением двух рёбер. Если удаляемые рёбра имеют общую вершину, то получится граф, который мы обозначим если рёбра не пересекаются, то их удаление даёт граф, который мы обозначим Так как все рёбра полного графа совершенно равноправны, то граф изоморфен одному из графов Графы и 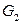не изоморфны друг другу, так как в графе 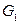есть вершина степени 9, а в графе 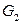таких вершин нет. Таким образом, имеется ровно 2 неизоморфных графа, удовлетворяющих условию задачи.