Нализ комбинационных схем методом p-алгоритма.

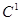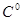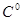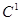При данном методе, как упоминалось выше, ищутся наборы входных переменных, обеспечивающих заданное значение на выходе КС. Наборы, обеспечивающие на выходе КС логическую 1, образуют так называемое единичное покрытие . Аналогично, входные наборы, обеспечивающие на выходе КС логический 0, образуют нулевое покрытие . Рассмотрим покрытия и для простейшего логического элемента 2И, выполняющего функцию Y=X₁X₂. Таблица истинности для этой функции представлена на рис.10.

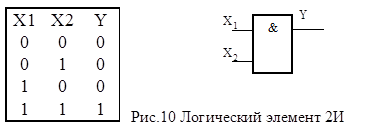Как видно из приведенной таблицы только при единственном наборе X₁=1 и X₂=1 на выходе ЛЭ будет 1, т.е. единичное покрытие включает только один набор 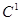={11}. На выходе ЛЭ будет 0 при трех наборах, образующих нулевое покрытие:

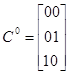
Это покрытие можно упростить, заметив, что первый набор склеивается со вторым и третьим, т.е.

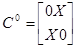
Т.о. для ЛЭ 2И можно сказать, что 1 на его выходе будет только при обеих единицах на входах, а для обеспечения 0 на выходе достаточно подать хотя бы на один вход 0. Рассуждая аналогично, получим таблицу покрытий и для основных ЛЭ, представленных в табл. 3.

Таблица 3

Покрытия С⁰ и С¹ для основных логических элементов

ЛЭ Y Y Y Y Y Y Y

НЕ 2И 2И – НЕ 2ИЛИ 2ИЛИ–НЕ ИСК. ИЛИ 3И – НЕ

X X₁ X₂ X₁ X₂ X₁ X₂ X₁ X₂ X₁ X₂ X₁ X₂ X₃

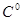1 0 X 1 1 0 0 1 X 0 0 1 1 1

X 0 X 1 1 1

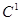0 1 1 0 X 1 X 0 0 0 1 0 X X

X 0 X 1 1 0 X 0 X

X X 0

При анализе схемы методом p - алгоритма, задавшись определенным значением на выходе, заменяют его соответствующим покрытием элемента, формирующего выходной сигнал. В результате этого определяется, какие должны быть сигналы на выходах элементов, подключенных к выходному ЛЭ. В свою очередь, сигналы на выходах этих элементов можно заменить соответствующими покрытиями, т.е. определить значения выходных сигналов для других ЛЭ и т.д. Этот процесс продолжается до тех пор, пока не получатся покрытия, состоящие только из входных переменных, называемых опорными. Совокупность таких покрытий и дает соответствующее покрытие схемы.

Пример анализа КС (рис 9. ) методом p - алгоритма представлен в табл. 4. В последней колонке этой таблицы приведен оператор подстановки, в результате работы которого сигнал на выходе ЛЭ заменяется соответствующим покрытием. Необходимо обратить внимание, что все значения переменных, записанные в одной строке, должны одновременно быть в наличии для обеспечения заданного значения выходного сигнала. Поэтому, при замене одного из значений в строке соответствующим покрытием, все остальные значения для других переменных в этой строке должны присутствовать совместно с этим покрытием.

На основании полученного единичного покрытия можно записать БФ, реализуемую схемой: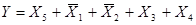

Таблица 4

Анализ схемы методом p – алгоритма.

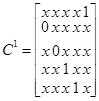
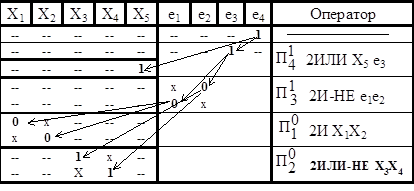
а) Получение единичного покрытия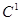

б) Получение нулевого покрытия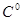

В дальнейшем можно сравнить полученную БФ с той, по которой строилась схема и проверить правильность ее построения. При анализе схемы может оказаться, что некоторая переменная, получившая на одном из предыдущих шагов некоторые значения на данном шаге должна принять противоположное значение. Возникшее противоречие говорит о том, что данный путь является тупиковым и его необходимо исключить из дальнейшего рассмотрения. Если ни при одной комбинации входных переменных не обеспечивается значение 1(0) на выходе, то это означает, что схема реализует константу 0(1) соответственно.