Пределы иррациональных выражений
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ ЗАДАНИЙ
Введение
Вычисление пределов функций начинают с непосредственной подстановки предельного значения основной переменной в выражении для функции, используя правила предельного перехода под знаком непрерывной функции, теоремы о пределах. Если получают неопределенности:
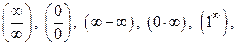
используют различные приемы их «раскрытия».
Ниже приведенное правило дет некоторые свойства бесконечно малых и бесконечно больших функций, связь между ними.
Правило 1.
Если
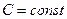 - (постоянная величина),
- (постоянная величина),
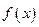 - ограниченная функция,
- ограниченная функция,
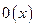 - бесконечно малая функция (или короче “0”),
- бесконечно малая функция (или короче “0”),
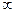 - бесконечно большая функция, то
- бесконечно большая функция, то
1) 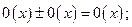 2)
2) 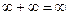 (
( 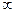 - одного знака);
- одного знака);
3) 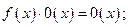 4)
4) 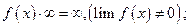
5) 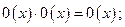 6)
6) 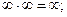
7) 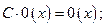 8)
8) 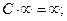
9) 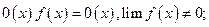 10)
10) 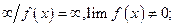
11) 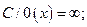 12)
12) 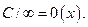
Таблица эквивалентных бесконечно малых функций при 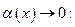
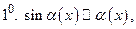
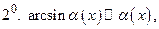
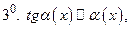
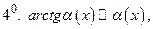
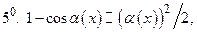
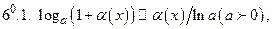
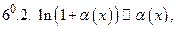
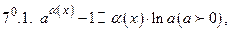
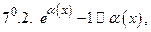
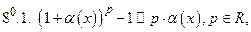
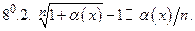
Примечание. Приближенными равенствами 6 и 8 пользуется в другой форме при 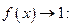
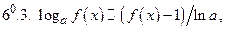
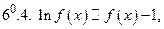
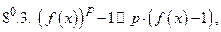
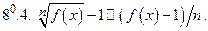
Правило 1.
При нахождении предела отношения бесконечно малых при бесконечно больших функций каждую из них (или одну) можно заменить другой функцией, ей эквивалентной. То есть:
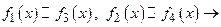
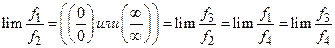 (1.1)
(1.1)
Правило 2.
Алгебраическая сумма бесконечно малых функций разных порядков эквивалентна слагаемому низшего порядка.
Правило 3.
Алгебраическая сумма бесконечно больших функций разных поряд-ков эквивалентна слагаемому высшего порядка.
Правило 4.
При вычислении предела показательно-степенной функции 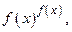 где
где 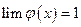 и
и 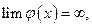
пользуются равенством:
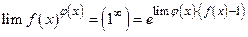 (1.2)
(1.2)
Правило 5.
Неопределенности вида 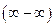 или
или 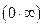 приводят к виду дроби, которая может дать новые – типа
приводят к виду дроби, которая может дать новые – типа 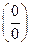 или
или 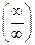 .
.
Часто используются при вычислении пределов следующие свойства показательной и степенной функции:
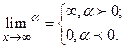 (1.3)
(1.3)
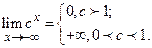 (1.4)
(1.4)
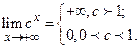 (1.5)
(1.5)
Пределы рациональных функций
Пример 1. 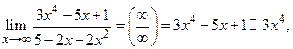
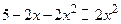 (Пр.4); Пр.2
(Пр.4); Пр.2 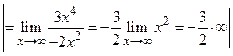 Пр. 1.8
Пр. 1.8 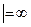
Пример 2. 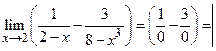 Пр. 1.11
Пр. 1.11 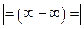 Пр. 6
Пр. 6 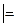
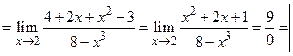 Пр. 1.11
Пр. 1.11 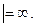
Пример 3. 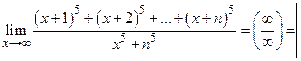 Пр. 4, Пр.2
Пр. 4, Пр.2 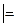
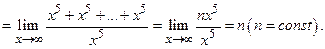
Пример4. 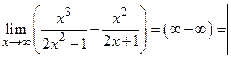 Пр.6
Пр.6 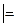
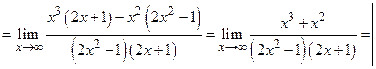 Пр.4,Пр.2
Пр.4,Пр.2 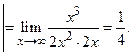
Примечание. Если бы мы воспользовались вначале последовательно правилами 4 и 2, то получили бы:
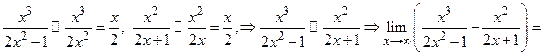
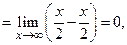
что неверно, так как разность эквивалентных бесконечно больших функций есть функция более низкого порядка, чем каждая из них (бесконечно большая, постоянная) как в рассмотренном примере, или, в крайнем случае, предел их разности может быть бесконечно малой функцией (см. пример 2 пункта. 2.4.2).
Пример 5. 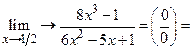 /разложим многочлены на множители/=
/разложим многочлены на множители/= 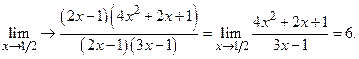
Пределы иррациональных выражений
Пример 1. 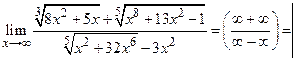 Пр. 4, Пр. 2
Пр. 4, Пр. 2 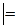
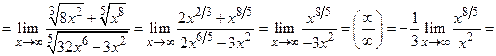
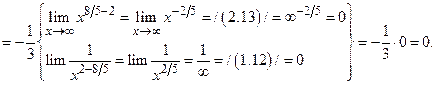
Примечание. При вычислении пределов иррациональных выражений, дающих неопределенности типа 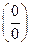 или
или 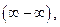 используют введение новой переменной, освобождающей от иррациональности, или преобразование выражения с помощью сопряженного ему. Например, парами взаимно сопряженных выражений будут:
используют введение новой переменной, освобождающей от иррациональности, или преобразование выражения с помощью сопряженного ему. Например, парами взаимно сопряженных выражений будут:
1) 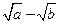 и
и 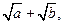
2) 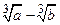 и
и 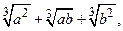
3) 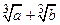 и
и 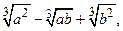 которые при вычислении пределов используются в формах:
которые при вычислении пределов используются в формах:
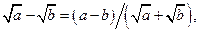 (1.6)
(1.6)
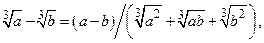 (1.7)
(1.7)
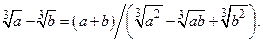 (1.8)
(1.8)
Пример 2. 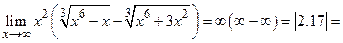
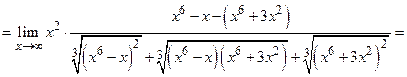
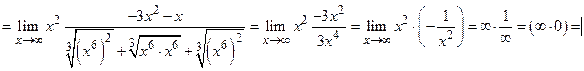 Пр.6
Пр.6 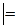
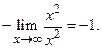
Пример 3. 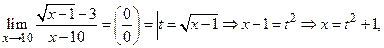
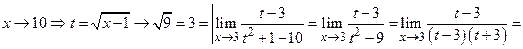
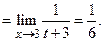
Пример 4. 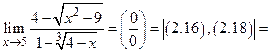
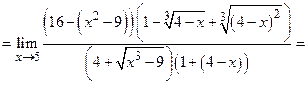
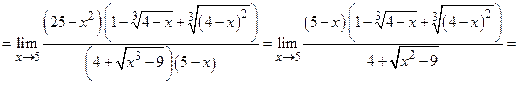
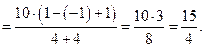
Примечание. Обратите внимание на то, что при вычислении предела 5 из пункта 2.4.I и 3,4 настоящего пункта, при раскрытии неопределенности 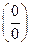 и
и 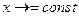 стараются так преобразовать выражение, чтобы дробь можно было сократить на множители
стараются так преобразовать выражение, чтобы дробь можно было сократить на множители 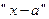 стремящийся к нулю.
стремящийся к нулю.
