Решение некоторых задач методом характеристик

Решим три задачи методом характеристик.

Задача 1 (Задача Коши)

Исходные данные: в физической плоскости XY на некоторой кривой АВ, которая не является характеристикой, задана скорость потока.

Требуется определить: скорости потока в области, ограниченной этой кривой и двумя характеристиками АС и ВС разных семейств (рис. 5.5), проведенных из точек А и В (эти характеристики строятся при решении задачи).

Решение: рассмотрим на кривой АВ ряд точек и проведем из каждой точки характеристики (линии возмущения) обоих семейств до их пересечения. – точки пересечения характеристик разных семейств (узловые точки). Ввиду малости участков разбиения характеристики можно считать прямолинейными. Уравнение отрезков этих прямых можно записать как уравнения прямых, проходящих через две точки:

и (5.20)

Координаты точек определим из выражений (5.20). Так, точка есть точка пересечения характеристики первого семейства, проведенной из точки , и характеристики второго семейства, проведенной из точки :

и . (5.21)

Скорость потока в узловых точках определим из уравнений соответствующих характеристик в плоскости годографа скорости, записанных через конечные разности. Так для точки они имеют вид

и . (5.22)

Система уравнений (5.21) позволяет определить координаты точ-ки . Решая систему уравнений (5.22). находим 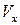и 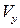в точке , а по ним и остальные параметры течения. Точно таким же образом определяются координаты всех других точек пересечения характеристик и находятся параметры течения в этих точках и т. д., пока не будут описаны подобным образом все точки рассматриваемой области течения. Крайние характеристики АС и ВС строятся в процессе решения задачи. Точность расчета зависит от количества выбранных точек на исходной кривой АВ (чем больше точек, тем выше точность).

Задача 2 (Задача Гурса)

Исходные данные: заданы скорости на двух характеристиках АВ и АС разных семейств, выходящих из точки А.

Требуется определить: поле скоростей в криволинейном четырехугольнике (рис. 5.6), ограниченном данными характеристиками и характеристиками ВD и СD, исходящими из точек В и С (определенных в процессе решения задачи).

Решение: Возьмем на АВ и АС ряд точек и . Тогда угловую точку найдем как точку пересечения линий возмущения разного семейства, проведенных из точек (второго семейства) и (первого семейства):

, .

Составляющие скорости в этой точке определим по уравнениям

и .

Затем определим координаты и составляющие скорости для точки и т. д. для всей четырехугольной области АВСD. Определив величины составляющих скорости, рассчитаем обычным порядком остальные параметры течения.

Задача 3

Исходные данные: заданы гидродинамические параметры на характеристике одного из семейств АВ и дана твердая стенка АС.

Требуется: определить параметры в треугольной области АВС (рис. 5.7), ограниченной твердой стенкой, заданной характеристикой АВ и характеристикой ВС,построенной в результате решения задачи.

Решение: возьмем на характеристике АВ ряд точек . Из точки проведем линию возмущения второго семейства до пересечения ее с твердой стенкой в точке . Координаты этой точки определим из совместного решения уравнений линии возмущения и заданной поверхности стенки y = y (x).

В точке направление скорости известно исходя из следующих соображений. При безотрывном обтекании стенки вектор скорости направлен вдоль касательной к стенке в точке (условие непротекания). То есть , и для нахождения составляющих скорости используем уравнения

и .

Затем, зная 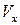и 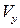в точке и , находим координату точки и составляющие скорости в ней, решая задачу Гурса. Координаты точки и значение скорости для нее определяем так же, как и для точки , и далее определяем параметры течения во всей искомой области АВС.

Обтекание сверхзвуковым потоком выпуклого угла

(течение Прандтля–Майера)

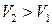Рассмотрим равномерный сверхзвуковой поток газа, движущийся со скоростью вдоль прямолинейной стенки АО. В точке О стенка отклоняется на угол от первоначального направления (рис. 5.8). В результате поворота сверхзвукового потока на угол скорость увеличивается ( ). Проведем из угловой точки О линию возмущения ОВ, угол наклона которой определится через известное соотношение (рис. 5.8, а).

а б

Рис. 5.8. Обтекание выпуклого угла сверхзвуковым потоком:

а – параметры течения в области I, II; б – параметры течения в области III

Линия ОВ – граница области возмущенного (III) и невозмущенного (I) движений. Так как в области I = const, то линия ОВ совпадает с характеристикой, и на основании задачи Гурса все характеристики этого семейства, исходящие из точки О, – прямые линии. Вдоль каждой такой прямой скорость постоянна по величине и направлению. Для потока, движущегося после поворота вдоль стенки ОС со скоростью , проведем линию возмущения (характеристику ОD) под углом к ОС, где . Линия ОD является нижней границей области возмущений III (ВОD), где происходит непрерывное изменение величины и направления вектора скорости от 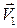до .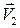

Найдем параметры течения в области возмущенного движения III (рис. 5.8, б).

Введем полярные координаты r и . За положительное направление отсчета угла будем считать направление по часовой стрелке. Разложим вектор скорости 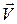на направления: r – вдоль радиуса (составляющая скорости ) и s – перпендикулярно радиусу (составляющая ). Вдоль характеристики, т. е. в направлении радиуса-вектора r, параметры течения газа неизменны, поэтому составляющие скорости и зависят только от угла .

Считая движение газа потенциальным, введем потенциал скорости и запишем выражения для составляющих скорости:

(5.23)

В качестве исходного уравнения для решения поставленной задачи запишем уравнение энергии (уравнение Бернулли) в виде

(5.24)

Как известно, составляющая вектора скорости в направлении, перпендикулярном к линии возмущения, всегда равна скорости звука , т. е. .

Рассмотрим производную , которая с учетом выражений (5.23) запишется в виде . Так как и не зависят от радиуса (равномерное поле скоростей), то . Следовательно, и .

Поэтому уравнение энергии (5.24) перепишется следующим образом:

или после преобразований: . Находя корни этого квадратного уравнения, будем иметь в виду, что в направлении течения скорость движения газа возрастает, т. е. . Поэтому получаем, что и после разделения переменных и интегрирования имеем следующее:

. (5.25)

Так как , то

. (5.26)

Для определения поля скоростей в области III (см. рис. 5.8) необходимо найти значение постоянной С. Воспользуемся граничным условием на линии возмущения ОВ.

При , . Поэтому и .

Отношение скоростей с привлечением уравнений (5.25) и (5.26) сводится к выражению

. (5.27)

Так как то и после преобразований выражения (5.27) получим выражение для определения произвольной постоянной:

. (5.28)

Значение произвольной постоянной С зависит от числа Маха набегающего потока . При постоянная принимает значение С = 0, в этом случае

и .

Установим зависимость между углом поворота потока и числом М. По аналогии с выражением (5.27) найдем отношение скоростей для промежуточной характеристики ОЕ:

.

Отсюда . Для характеристики ОЕ , и учитывая, что , получим .

Тогда зависимость угла поворота потока от числа Маха примет следующий вид:

. (5.29)

Сравнение формул для и С указывает на их абсолютную идентичность, поэтому С можно трактовать как угол поворота звукового потока до получения заданного числа . Поскольку этот поворот произошел вне рамок данной задачи, то его принято называть фиктивным углом поворота потока и обозначать через (рис. 5.9).

Тогда уравнение (5.29) примет вид

. (5.30)

Это уравнение совпадает с уравнением эпициклоиды (5.19) (характеристики в плоскости годографа скорости). Следовательно, при обтекании угла, большего по известной величине можно найти скорость течения, пользуясь сеткой эпициклоид.

Для проведения инженерных расчетов составлены таблицы изоэнтропических течений, идущих с непрерывным увеличением скорости. В основу положена зависимость угла поворота потока (5.30) от числа Маха после окончания разворота ( ). Поскольку каждому значению числа Маха в начале разворота потока соответствует свое значение фиктивного угла , то при определении угла поворота потока или для каждого значения пришлось бы иметь свои таблицы. Так как расчетные формулы для угла поворота потока и абсолютно идентичны, то при составлении таблиц учли это обстоятельство. В таблицах приведены значения параметров потока при повороте звукового ( = 1) потока на угол . Тогда при > 1 сначала определяют (из этих же таблиц) как угол поворота, при котором происходит разгон потока от М = 1 до М = . Затем по суммарному углу находят и по соотношениям для изоэнтропических течений рассчитывают другие параметры: .

Максимальный угол поворота представляет собой угол поворота звукового потока ( = 1, C = 0) до получения им скорости (при расширении до абсолютного вакуума, p = 0 ). Из уравне-ния (5.30) при указанных условиях . Для воздуха (k = 1,4) .

Предельный угол поворота – это угол, на который может повернуть сверхзвуковой поток ( > 1) при его истечении в вакуум. В соответствии с формулой (5.30) . Для набегающего потока, число Маха которого равно = 1, , а для = , .

Таким образом, рассмотренные сверхзвуковые течения с непрерывным увеличением скорости происходят плавно, без каких-либо особенностей. В то же время уменьшение скорости сверхзвукового потока и переход через скорость звука происходит скачкообразно.

Контрольные вопросы и задания

1. Что означает потенциальность потока (течения) газа? Что является критерием потенциальности плоского изоэнтропического потока газа?

2. Что, по сути, представляет собой основное дифференциальное уравнение газовой динамики для плоского потенциального установившегося газового потока?

3. Какие методы применяются для решения дифференциального уравнения газовой динамики для плоского потенциального установившегося газового потока? Для какого диапазона скоростей используются данные методы? В чем сущность линеаризации уравнения с помощью метода малых возмущений?

4. Что представляют собой характеристики в физической плоскости, в плоскости годографа скорости? Сколько характеристик можно провести через каждую точку пространства в сверхзвуковом потоке, в дозвуковом?

5. Как располагаются относительно друг друга характеристики в плоскости потока и в плоскости годографа скорости?

6. Опишите порядок решения некоторых краевых задач для сверхзвуковых потенциальных течений газа: задачи Коши, задачи Гурса, задачи сверхзвукового обтекания тела при известных параметрах на характеристике одного из семейств.

7. Дайте определение фиктивного, предельного и максимального углов поворота потока. Как влияют физические свойства газа на их величины? Почему сверхзвуковой поток можно повернуть на угол меньший, чем звуковой поток?

8. Сверхзвуковой поток обтекает выпуклый плоский угол (угол больший 180^о). Как при этом изменяются скорость течения и параметры газа ?

9. Чему равна составляющая вектора скорости в направлении, перпендикулярном к линии возмущения?

10. Сверхзвуковой воздушный поток, обтекая выпуклый угол АОС (см. рис. 5.8), ускоряется. При числе Маха набегающего потока М₁ = 1,5 число Маха уходящего потока равно М₂ = 3. На какой угол повернул поток?