Упражнения для самостоятельного решения
1. Сколько всего: а) связных графов на множестве из 3 вершин; б) неизоморфных графов на множестве из 4 вершин? Ответ: а) 2; б) 11.
2. Сколько всего неизоморфных деревьев с 6 вершинами? Ответ: 6.
3. Сколько всего неизоморфных графов, имеющих 10 вершин, а количество рёбер равно: а) 45; б) 44; в) 43? Ответ: а) 1; б) 2; в) 2.
4. Сколько компонент связности может иметь граф, у которого 12 вершин и 40 рёбер? Ответ: 1,2,3.
5. Построить матрицу смежности и матрицу инцидентности графов, изображённых на рисунке.
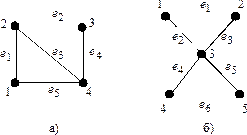
Ответ: а) 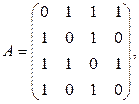
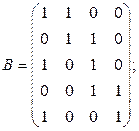
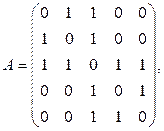
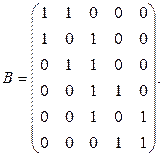
6. Изобразить граф, имеющий следующую матрицу смежности: а) 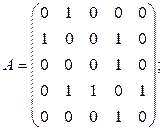 б)
б) 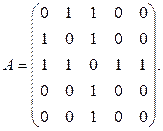
Ответ:
7. Изобразить граф, имеющий следующую матрицу инцидентности: а) 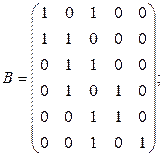 б)
б) 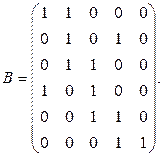
Ответ:
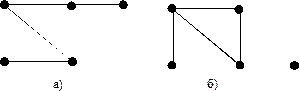
8. Является ли связным граф со следующей матрицей смежности: 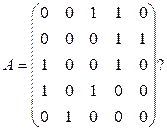 Ответ: нет.
Ответ: нет.
9. Существует ли граф со следующим набором степеней вершин: а) 1,1,1,2,2,3,3; б) 1,1,2,2,2,3,3,4? Ответ: а) нет; б) да.
10. Пусть  – граф. Противоположным графом назовём граф
– граф. Противоположным графом назовём граф 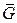 с тем же множеством вершин, что и у
с тем же множеством вершин, что и у  причём
причём 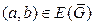
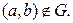 Доказать, что если граф
Доказать, что если граф  несвязный, то граф
несвязный, то граф 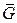 связный.
связный.
11. Доказать, что граф с 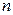 вершинами, имеющий более
вершинами, имеющий более 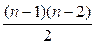 рёбер, является связным.
рёбер, является связным.
12. Построить двоичный код дерева (начало обхода помечено крестиком и стрелкой):
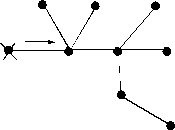
Ответ: (0010100101001111).
13. Построить код Прюфера дерева
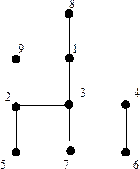
Ответ: [2343311].
14. Построить дерево по его двоичному коду: (0010010010111011).
Ответ:
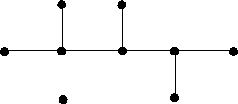
15. Построить дерево по его коду Прюфера: [2442778].
Ответ:
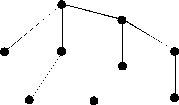
16. Построить базис пространства циклов графа, изображённого на рисунке.
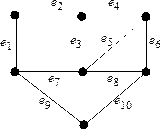
Ответ: 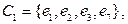
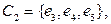
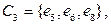
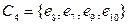 (ответ неоднозначен).
(ответ неоднозначен).
17.  В графе
В графе 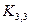 рассмотрим цикл
рассмотрим цикл 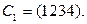 Дополнить его до базиса пространства циклов. Ответ: например, так:
Дополнить его до базиса пространства циклов. Ответ: например, так: 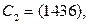
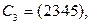
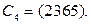
18. Чему равна размерность пространства циклов графа 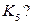 Сколько в
Сколько в 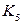 всего обобщённых циклов? Ответ: 6; 64.
всего обобщённых циклов? Ответ: 6; 64.
19. Сколько компонент связности имеет лес, у которого 25 вершин и 11 рёбер? Ответ: 14.
20. Сколько граней имеет планарный граф, у которого 12 вершин и 30 рёбер? Ответ: 20.
21. Являются ли планарными графы: а) 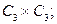 б)
б) 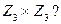 Ответ: а) да; б) нет.
Ответ: а) да; б) нет.
22. Граф представляет собой трёхмерный куб, в котором проведена диагональ. Планарен ли этот граф? Ответ: нет.
23. Сколько рёбер следует удалить из графа 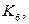 чтобы получилось дерево? Ответ: 25.
чтобы получилось дерево? Ответ: 25.
24. Чему равно наименьшее количество рёбер, удаление которых из графа 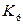 делает граф несвязным? Ответ: 5.
делает граф несвязным? Ответ: 5.
25. Чему равно наименьшее число 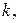 обладающее свойством: удаление из графа
обладающее свойством: удаление из графа 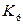 любых
любых 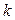 рёбер делает граф несвязным? Ответ: 26.
рёбер делает граф несвязным? Ответ: 26.
26. Связный планарный граф без петель, висячих вершин и кратных рёбер имеет 6 вершин. Сколько рёбер может иметь этот граф? Ответ: 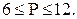
27. Связный планарный граф без петель, висячих вершин и кратных рёбер имеет 5 вершин. Сколько граней может быть в его плоской укладке? Ответ: 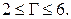
28. Связный планарный граф без петель и висячих вершин имеет 19 рёбер. Сколько граней может быть в его плоской укладке? Ответ: 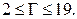
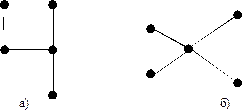
29. Найти хроматическое число графа, изображённого на рисунке
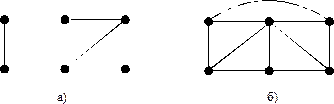
Ответ: а) 3; б) 4.
30. Найти рёберное хроматическое число следующих графов: а) 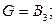 б)
б) 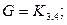 в)
в)  состоит из вершин и рёбер октаэдра. Ответ: а) 3; б) 4; в) 5.
состоит из вершин и рёбер октаэдра. Ответ: а) 3; б) 4; в) 5.
31. Верно ли, что 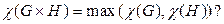 Ответ: да.
Ответ: да.
