Исследование характеристик детализированных структурных схем.
Целью лабораторной работы является освоение методики составления детали-
зированных структурных схем и сравнения временных и частотных характеристик обычных и детализированных структурных схем.
3.1. Краткие теоретические сведения.
Детализированной структурной схемой (ДСС) называется схема, состоящая только из интегрирующих и масштабных звеньев с полностью вскрытыми связями между ними.
Детализированные структурные схемы являются наилучшим исходным материалом для составления векторно-матричного описания АСУ.
Существует три способа составления ДСС.
1. Исходное дифференциальное уравнение звена или участка схемы составляется
в нормализованной форме Коши, от которой очень просто перейти к ДСС.
 Рассмотрим в качестве примера запись уравнения электромагнитной цепи (рис 3.1,а).
Рассмотрим в качестве примера запись уравнения электромагнитной цепи (рис 3.1,а).
Уравнение напряжений в этой цепи: 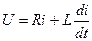 . Перепишем это уравнение в
. Перепишем это уравнение в
нормализованной форме Коши: 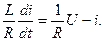 Обозначим:
Обозначим: 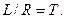 Получим
Получим 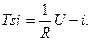 . И, окончательно,
. И, окончательно, 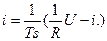 . ДСС, реализующая полученное уравнение, представлена на рис. 3.1,б.
. ДСС, реализующая полученное уравнение, представлена на рис. 3.1,б.
2. ДСС типового динамического звена может быть получена путем преобразования исходной передаточной функции с помощью правил преобразования структурных схем. Например, звено с передаточной функцией 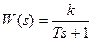 может быть представлено произведением двух передаточных функций:
может быть представлено произведением двух передаточных функций: 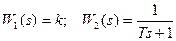 . Вторая передаточная функция может быть записана как
. Вторая передаточная функция может быть записана как 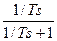 , которая соответствует
, которая соответствует
передаточной функции замкнутой структуры, состоящей из интегратора 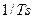 , замкнутого единичной обратной связью. В результате приходим к ДСС (рис. 3.2).
, замкнутого единичной обратной связью. В результате приходим к ДСС (рис. 3.2).
 |
3. ДСС может быть также получена преобразованием операторного уравнения звена относительно выходной величины через операторы интегрирования и масштабного преобразования. Пусть исходная передаточная функция имеет вид:
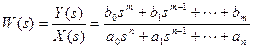 .
.
Преобразование будем вести в следующей последовательности.
3.1. Записываем уравнение, выполняя умножение «крест-накрест»:
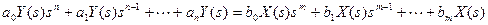 .
.
3.2. Разрешаем уравнение относительно старшей производной выходной величины: 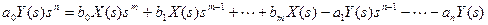 .
.
3.3. Делим обе части уравнения на коэффициент при 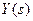 в левой части уравнения:
в левой части уравнения: 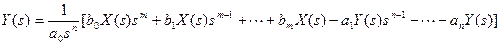
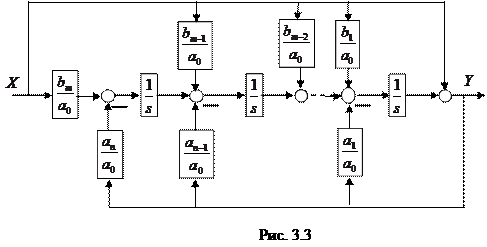
3.4. Строим структурную схему согласно последнего выражения, так как при
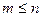 в правой части окажутся только операторы интегрирования и суммирования (рис. 3.3).
в правой части окажутся только операторы интегрирования и суммирования (рис. 3.3).
 |
Рассмотрим применение приведенной последовательности для составления ДСС
корректирующего звена с передаточной функцией 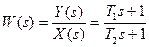 .
.
1) 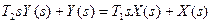 ; 2)
; 2) 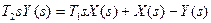 ;
;
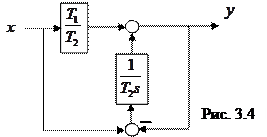 3)
3) 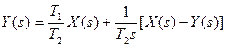 ; 4)
; 4)
Составим ДСС устойчивого колебательного звена 2-го порядка, используя вышеприведенную методику. 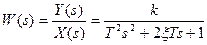 .
.
1) 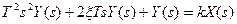 ; 2)
; 2) 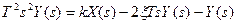
3.2. Программа выполнения работы.
1. Открыть рабочее окно SIMULINK. По параметрам, заданным преподавателем,
(смотри таблицу) создать модель апериодического звена 1-го порядка. Вывести в отчет в одном окне четыре характеристики: ПХ, ИПХ, ЛАФЧХ, АФХ с отмеченными параметрами характе-ристик.
2. Заменить в рабочем окне общую модель детализированной. Выполнить ту же последовательность операций по выводу характеристик в отчет.
3. Проделать операции п.п. 1 и 2 с корректирующим звеном для двух вариантов
параметров: 1) 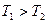 (дифференцирующий характер звена); 2)
(дифференцирующий характер звена); 2) 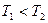 (интегрирующий характер звена). Убедившись в идентичности общей и детализированной схем, вывести
(интегрирующий характер звена). Убедившись в идентичности общей и детализированной схем, вывести
характеристики в отчет.
4. По параметрам, заданным в таблице, реализовать модель звена 2-го порядка, в общем и детализированном виде. В случае совпадения характеристик обоих
моделей вывести схемы и графики в отчет.
4. Провести исследование влияния коэффициента демпфирования на вид характеристик Боде и Найквиста.
Таблица
| Вариант | Апериодическое звено 1-го порядка 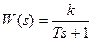 | Корректирующее звено 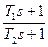 | Колебательное звено 2-го порядка 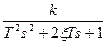 | ||||
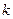 | 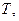 сек сек | 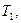 сек сек | 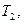 сек сек | 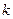 | 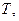 сек сек | 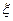 | |
| 0,5 | 0,25 | 0,1 | 0,6 | 0,5 | 0,5 | 0,2 | |
| 1,0 | 0,5 | 0,2 | 0,7 | 0,75 | 0,7 | 0,3 | |
| 1,5 | 0,75 | 0,3 | 0,8 | 1,0 | 0,9 | 0,4 | |
| 2,0 | 1,0 | 0,4 | 0,9 | 1,25 | 1,1 | 0,5 | |
| 2,5 | 1,25 | 0,5 | 1,0 | 1,5 | 1,3 | 0,6 | |
| 3,0 | 1,5 | 0,6 | 0,1 | 1,75 | 1,5 | 0,7 | |
| 3,5 | 1,75 | 0,7 | 0,2 | 2,0 | 1,7 | 0,8 | |
| 4,0 | 2,0 | 0,8 | 0,3 | 2,25 | 1,9 | 0,75 | |
| 4,5 | 2,25 | 0,9 | 0,4 | 2,5 | 2,1 | 0,8 | |
| 5,0 | 2,5 | 1,0 | 0,5 | 3,0 | 2,3 | 0,9 |
2.3. Содержание отчета.
2.3.1 название, цель и содержание работы;
2.3.2. описание операций выполнения программы работы;
2.3.3. копии всех схем и графиков, созданных в ходе выполнения работы, снабженных соответствующими формулами из теоретического раздела;
2.3.4. выводы по работе.
Лабораторная работа №4
Исследование устойчивости линейных АСУ с помощью основных критериев устойчивости.
Целью лабораторной работы является изучение возможностей оценки устойчи-вости линейных АСУ средствами компьютерной системы SIMULINK – MATLAB с помощью известных критериев устойчивости: Гурвица, Михайлова, Найквиста.
4.1. Краткие теоретические сведения.
Как известно, главным условием устойчивости замкнутой системы управления является расположение корней характеристического уравнения замкнутой системы в левой полуплоскости плоскости корней. Положения, позволяющие судить, находятся ли корни характеристического уравнения в левой полуплоскости, называются критериями устойчивости.
Среди разработанных в настоящее время критериев наибольшее применение нашли критерии Гурвица, Михайлова и Найквиста.
Критерий Гурвица базируется на анализе знаков коэффициента 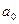 характеристического уравнения замкнутой системы и знаков диагональных миноров матрицы Гурвица, составленной из коэффициентов характеристического уравнения.
характеристического уравнения замкнутой системы и знаков диагональных миноров матрицы Гурвица, составленной из коэффициентов характеристического уравнения.
Критерий гласит: чтобы замкнутая система была устойчивой, необходимо и достаточно, чтобы при 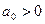 все диагональные миноры матрицы Гурвица были положительными.
все диагональные миноры матрицы Гурвица были положительными.
Критерий Михайлова построен на анализе прохождения годографа характеристического полинома замкнутой системы в комплексной плоскости при изменении частоты в диапазоне 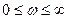 . Согласно критерия Михайлова, замкнутая система будет устойчива, если годограф характеристического уравнения замкнутой системы при изменении частоты в диапазоне
. Согласно критерия Михайлова, замкнутая система будет устойчива, если годограф характеристического уравнения замкнутой системы при изменении частоты в диапазоне 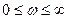 обходит в положительном направлении
обходит в положительном направлении 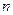 квадрантов комплексной плоскости, не пересекаясь нигде сам с собой и не обращаясь в нуль. Здесь
квадрантов комплексной плоскости, не пересекаясь нигде сам с собой и не обращаясь в нуль. Здесь 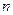 - порядок характеристического уравнения. Если годограф характеристического полинома проходит через начало координат, система управления находится на границе устойчивости.
- порядок характеристического уравнения. Если годограф характеристического полинома проходит через начало координат, система управления находится на границе устойчивости.
Критерии Гурвица и Михайлова используют для своей работы информацию о замкнутой системе управления (годограф характеристического полинома это левая часть характеристического уравнения замкнутой системы, в которой 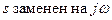 ).
).
Критерий Найквиста использует амплитудно-фазовую частотную характеристику разомкнутой системы, которая может быть получено либо экспериментально, либо аналитически из передаточной функции разомкнутой системы заменой 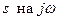 .
.
Формулировка критерия Найквиста весьма проста: если разомкнутая система устойчива, то для устойчивости её в замкнутом состоянии необходимо и достаточно, чтобы амплитудно-фазовая частотная характеристика разомкнутой системы не охватывала критическую точку с координатами 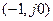 при изменении частоты в диапазоне
при изменении частоты в диапазоне 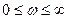 . Прохождение амплитудно-фазовой частотной характеристики через критическую точку
. Прохождение амплитудно-фазовой частотной характеристики через критическую точку 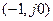 означает, что замкнутая система будет находиться на границе устойчивости. И если амплитудно-фазовая характеристика пересекает отрицательную вещественную ось левее критической точки
означает, что замкнутая система будет находиться на границе устойчивости. И если амплитудно-фазовая характеристика пересекает отрицательную вещественную ось левее критической точки 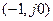 , то замкнутая система будет неустойчивой.
, то замкнутая система будет неустойчивой.
4.2. Программа выполнения работы.
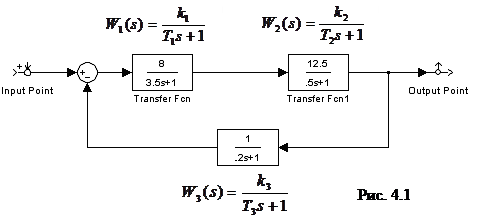
1. Создать в рабочем окне модель автоматической системы управления 4-го порядка по образцу модели, представленной на рис. 4.1. Параметры модели задаются преподавателем согласно таблице.
Таблица
| Вар. | 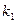 | 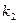 | 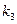 | 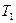 , сек , сек | 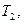 сек сек | 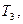 сек сек |
| 0,1 | 0,05 | |||||
| 1,5 | 0,2 | 0,05 | ||||
| 1,2 | 2,5 | 0,5 | 0,05 | |||
| 0,5 | 0,05 | |||||
| 1,5 | 3,5 | 0,25 | 0,05 | |||
| 3,5 | 0,25 | 0,1 | ||||
| 12,5 | 1,5 | 0,4 | 0,1 | |||
| 17,5 | 4,5 | 0,4 | 0,1 | |||
| 22,5 | 4,5 | 0,75 | 0,1 | |||
| 1,5 | 0,75 | 0,1 |
2. Построить переходную характеристику системы управления и убедиться, что система управления является неустойчивой. Построить диаграммы Боде и Найквиста и
показать, что обе они свидетельствуют о неустойчивом состоянии системы.
3. Записать характеристическое уравнение замкнутой системы
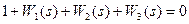
и представить его в форме полинома 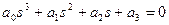 . Для системы 3-го порядка
. Для системы 3-го порядка
матрица Гурвица имеет вид: 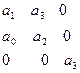 . Кроме положительности всех коэффициентов
. Кроме положительности всех коэффициентов
необходимо выполнить неравенство 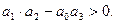 . Приравняв нулю это неравенство,
. Приравняв нулю это неравенство,
находим значение 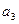 , при котором система будет находиться на границе устойчивости.
, при котором система будет находиться на границе устойчивости.
Коэффициент передачи разомкнутой системы, соответствующий границе устойчивости,
называется критическим коэффициентом усиления системы управления.
4. Вставить найденное значение критического коэффициента в модель и построением переходной характеристики, диаграмм Боде и Найквиста доказать, что система действительно находится на границе устойчивости. Переходную характеристику, диаграммы Боде и Найквиста скопировать в отчет.
5. Подобрать значение общего коэффициента передачи разомкнутой системы,
обеспечивающее переходную характеристику с максимальным перерегулированием не
более 30%. Вывести схему системы с подобранными параметрами, переходную характеристику, диаграммы Боде и Найквиста в отчет.
1.6. Содержание отчета.
Отчет должен содержать:
1.6.1 название, цель и содержание работы;
1.6.2. расчет критического и настроечного коэффициента усиления системы;
1.6.3. копии всех схем и графиков, созданных в ходе выполнения работы;
1.6.4. выводы по работе.
