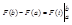Интегрирование по частям и замена переменной в неопределенной интеграле

Замена переменной.

Будем полагать функции f(u) и φ'(x) непрерывными. Замена переменной производится по формуле:

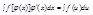
Формула проверяется дифференциалом обеих частей равенства по x (правая часть дифференцируется как сложная функция).

Интегрирование по частям:

Пусть u и v являются функциями x. Умножив обе части равенства (uv)'=u'v+uv' на dx, получим d(uv)=vdu+udv. Интегрируя приходим к формуле интегрирования по частям

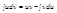
40. Интеграл с переменным верхним пределом. Теорема о его непрерывности.

Теорма: Если функция f(x) интегрируема на отрезке [a,b], то функция

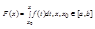
непрерывна на этом отрезке.

Доказательство: Дадим числу х приращение ∆х так, чтобы х+∆хÎ[a,b]. Для наглядности изобразим на числовой оси один из возможных вариантов расположения точек:

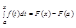a x₀ x х+∆х b

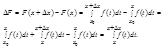
Получим:

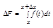По теореме (Если функция y=f(x) интегрируема на отрезке, то интегрируема и абсолютная величина |f(x)|, причем

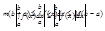…(на этом теорема закончилась, но неравенство относится к ней.) и следствию из теоремы (Если на отрезке [a,b] функция f(x) интегрируема и удовлетворяет неравенству m£f(x)£M. То выполняются неравенства:

(на этом следствие из теоремы закончилось)

получаем:

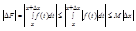Отсюда следует, что при ∆х→0 будет ∆F→0. Это доказывает непрерывность функции F(x). Отметим, что для подынтегральной функции f(x) точка х может быть точкой разрыва.

Теорема о произвольной от интеграла с переменным верхним пределом.

Теорема: Если функция y=f(x) непрерывна на промежутке (a,b), то производная от интеграла

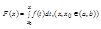
По переменному верхнему пределу x существует и равна подынтегральной функции с заменой переменной интегрирования верхним пределом х, т.е. F'(x)=f(x)

Доказательство: Дадим аргументу х приращение

∆х так, чтобы х+∆хÎ(a,b). Для приращения ∆F функции F(x) воспользуемся формулой

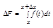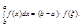и применим теорему о среднем значении ( Если функция y=f(x) непрерывна на отрезке [a,b], то найдется такая точка ξÎ (a,b), что справедливо равенство:

Теорема верна и при b<a.) получим:

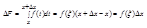
Число x заключено между числами х и х+∆х и при стремлении ∆х к нулю ξ стремится к х.

Перейдем к вычислению производной F'(x).

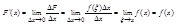
Последнее равенство основано на непрерывности функции f(x) в любой точке х промежутка (a,b).

Следствие: Всякая функция f(x), непрерывная на промежутке (a,b), имеет первообразную на этом промежутке.

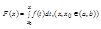Действительно, первообразной для такой функции является функция

Предыдущая теорема устанавливает связь между неопределенным и определенным интегралом. Можно написать:

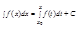
Формула Ньютона-Лейбница.

Пусть F(x) -произвольная первообразная для функции f(x), заданной на промежутке [a,b]. Так как две первообразные одной и той же функции отличаются на постоянное слагаемое, то верно равенство (1):

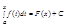
( в качестве числа х₀ взято число а).

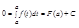В этом тождестве положим х=а и получим ,

Откуда С = -F(a). Формула (1) примет вид:

Заменяя здесь х на b, приходим к формуле Ньютона-Лейбница:

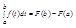
Иногда ее правую часть записывают короче с помощью двойной подстановки: