Измерениях

Наиболее простыми, но распространенными случаями зависимости между аргументами при косвенных измерениях являются случаи линейной зависимости, степенных одночленов и дифференциальной функции.

В случае линейной зависимости

(3.34)

Рисунок 3.7. Алгоритм обработки результатов косвенных измерений.

не требуется проведения линеаризации выражения для погрешности, которое, очевидно будет иметь вид

.

То есть, вместо коэффициентов влияния можно использовать коэффициенты из выражения (3.34).

Дальнейшее определение погрешности измерения будет производиться аналогично косвенным измерениям с линеаризацией.

В случае зависимости в виде степенных одночленов уравнение измерения будет иметь вид

. (3.35)

Рисунок 3.7 - Алгоритм обработки результатов косвенных измерений

Из этого выражения можно определить коэффициенты влияния

. (3.36)

Подставляя (3.36) в (3.35) и деля обе части на 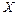, получаем искомую относительную погрешность

, (3.37)

где - относительные погрешности измерения аргументов.

Таким образом, в случае уравнения измерения в виде степенных одночленов и представлении погрешностей в относительной форме, в качестве коэффициентов влияния берутся степени соответствующих одночленов.

Практический прием нахождения коэффициентов влияния при выражении погрешностей в форме относительных погрешностей состоит в том, что уравнение измерения сначала логарифмируют, а потом дифференцируют. В рассматриваемом случае

;

.

То есть полученное выражение аналогично (3.37).

В метрологии часто встречается дифференциальная функция вида

Дисперсия результата измерения в этом случае будет равна

.

Малое значение дисперсии может быть только в случае, когда в этом случае а при

Во всех остальных случаях 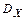отлично от нуля. При отсутствии корреляции Максимальное значение дисперсии результата измерения будет в том случае, когда в этом случае Таким образом, при измерении малых разностей дисперсия результата измерения может быть соизмерима с самим результатом измерения.