Одна загальна схема регресійного аналізу. Метод найменших квадратів
ВСТУП
Регресійний аналіз є одним з найголовніших методів сучасної математичної статистики. Ідея регресійного аналізу грунтується на тому положенні, що всі доступні для для дослідника ресурси слід використовувати повністю і ефективно, особливо якщо мова йде про накопичення і переробку інформації.
В сучасній промисловості, зокрема, в легкій промисловості в інформації немає нестачі. Показники приборів говорять нам про такі речі, як початкова температура, концентрація реагента, процент каталізатора, температура пари, швидкість витрачання речовини, степінь накопичення пошкодження, тиск і т.п., в залежності від характеристик процеса в даному дослідженні.
В першому наближенні можна вважати, що сучасний регресійний аналіз становить собою сукупність алгебраїчних процедур мінімізації квадратичної форми, що є, по суті методом найменших квадратів і систему статистичних постулатів, що задає математичну модель. Відповідні обчислення, особливо у випадку багатьох факторів (багатовимірна модель) потребують застосування або спеціальної розробки належних комп’ютерних програм. Це стосується як питань оцінювання параметрів моделі досліджуваного явища або процесу, так і перевірки статистичних гіпотез, що пов’язані із з’ясуванням питання про якість створеної моделі. Цей аспект знайшов відображення у даній методичній розробці завдяки розміщенні у ній опису кількох лабораторних робіт з застосуванням спеціалізованого програмного забезпечення. Нарешті, зауважимо, що дана частина розробки присвячена, в основному, “одновимірному” регресійному аналізу, який є досить важливим як з точки зору застосувань, так і завдяки можливості висвітлити основні ідеї регресійного аналізу, не затемнюючи їх технікою, що вживається при застосуванні багатофакторних моделей і яка, як свідчить досвід викладання, сама по собі може складати певні труднощі для студентів нематематичних спеціальностей.
ТЕОРЕТИЧНІ ПОЛОЖЕННЯ
РОЗДІЛ 1. ПРО ПОСТАНОВКУ ЗАДАЧ РЕГРЕСІЙНОГО АНАЛІЗУ
Попередні відомості
В багатьох експериментальних дослідженнях ми хочемо дізнатися, як зміни однієї величини впливають на іншу величину. Інколи дві змінні пов’язані точним функціональним співвідношенням. Наприклад, якщо опір R простого електричного ланцюга підтримується сталим, то струм I змінюється лінійно при лінійній зміні напруги V у відповідності із законом Ома I = V/R. Якби ми не знали закону Ома, то могли б знайти залежність емпірично, змінюючи V і вимірюючи R. Тоді ми побачили б, що графік залежності I від V наближено задається прямою лінією, що проходить через початок координат. Зазначена наближеність має місце з тієї причини, що наші виміри можуть містити певні похибки, і тому точки на графіку, скоріш за все, не розмістяться точно на одній прямій, хоча залежність фактично є точною. Іноді функціональна залежність принципово не є точною, навіть якщо не враховувати помилки. Наприклад, нехай розглядається зріст і вага дорослих чоловіків, обраних випадковим чином у деякій місцевості. Якщо ми нанесемо на графік пари чисел (Y1,Y2) = (зріст, вага), то результат у якісному відношенні буде відповідати наведеному нижче рис. 1.1. Відзначимо, що тут немає ніякого сенсу займатися підбором точної функціональної залежності між Y1 та Y2 (так щоб відповідний графік пройшов через всі експериментальні точки). І справа навіть не в тому, що така залежність була б надто складною. Більш істотне значення має та обставина, що при повторенні експерименту заново отримані експериментальні значення напевне не розташуються в точності на зазначеному графіку. Тож у даній ситуації слід підбирати математичну модель зв’язку між змінними не в формі точної залежності, а в формі залежності наближеної, яка, не маючи надто складного вигляду, належним чином відтворила би найбільш суттєві тенденції зв’язку між досліджуваними змінними. Крім того, бажано було б одержати ще ймовірнісну оцінку похибки підібраної залежності. Математичні моделі зв’язків між змінними зазначеного типу часто називають регресійними моделями або моделями регресії (нижче будуть наведені уточнення поняття регресійної моделі, а також роз’яснення терміну “регресія” у даному контексті). Зауважимо, що у даному разі в якості такої моделі доцільно обрати залежність першого порядку (пряма лінія на рис. 1.1).
               Вага (Y2) | |
| Зріст (Y1) | |
Рис. 1.1. Зріст та вага 17 дорослих чоловіків (скомпільоване з монографії [])
Одна загальна схема регресійного аналізу. Метод найменших квадратів
Нехай досліджується зв’язок між групою змінних x1,…xp та змінною y. При цьому вважається, що змінним x1,…xp можна надавати довільних значень (принаймні в певному діапазоні), а значення змінної y залежать від значень x1,…xp і одержуються експериментальним шляхом. Одна з найбільш загальних і важливих задач математичної статистики полягає у створенні математичної моделі, що описує (пояснює) вищезазначений зв’язок. Самі математичні моделі можуть бути різними. Наприклад, це можуть бути явні залежності, диференційні або інтегральні рівняння тощо. В регресійному аналізі застосовуються так звані регресійні моделі (моделі регресії). Однією з найпоширеніших регресійних моделей є модель у вигляді залежності
y = g(x1,…xp; b1,…,bm) + e , (1.1)
в якій g – деяка функція, b1,…,bm – параметри залежності, e – випадкова величина з нульовим математичним сподіванням. У відповідності із поширеною термінологією змінні x1,…xp звуться незалежними змінними або регресорами, змінна y – залежною змінною або предиктором, функція g – функцією регресії.
Основні задачі, що виникають при підборі (підгонці) регресійної залежності до експериментальних даних за допомогою моделі (1.1), формулюються наступним чином.
1. Обрати конкретну функцію g.
2. Оцінити (наближено визначити) параметри b1,…,bm.
3. Перевірити адекватність (більш широко – можливість або доцільність застосування) обраної (побудованої) моделі.
4. Визначити ймовірнісні властивості випадкової складової e, зокрема, оцінити її дисперсію (останнє – з метою визначення можливих відхилень залежної змінної y = y(x1,…xp) від значень функції регресії g(x1,…xp; b1,…,bm)).
5. Застосувати обрану модель для конкретних розрахунків і оцінити можливі похибки, що можуть виникнути при цьому.
Перейдемо до обговорення можливостей розв’язку сформульованих задач.
1. Суто математичні методи відіграють лише допоміжну (хоча і важливу) роль в задачі вибору фунції g. З повною надійністю такий вибір може бути зроблено лише за допомогою змістовних міркувань, що спираються на суть розглянуваного явища, його фізичний зміст. На жаль, досить часто зазначені міркування буває дуже важко навести, і тоді у першому наближенні задовольняються таким вибором функції g, який підказано графічним зображенням даних або діапазоном зміни незалежних змінних тощо. Якщо припустити, що вибір фунції g вже виконано, то можна перейти до другої з вищесформульованих задач.
2. Найчастіше оцінка невідомих параметрів у регресійному аналізі виконується за методом найменших квадратів (скорочено: МНК). Суть методу полягає в наступному. Нехай виконується n експериментів, в кожному з яких вектору незалежних змінних x = (x1,…xp) надається певних значень, і при цьому одержуються деякі значення залежної змінної y. Позначимо xi = (xi1,…, xip) набір значень назалежних змінних, що було надано їм в i-му експерименті, yi – відповідні значення залежної змінної (i = 1,2,…, n). Згідно з МНК в якості оцінки вектора параметрів b = (b1,…,bm) береться такий вектор b = (b1,…, bm) (інше позначення –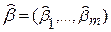 
) при якому сума
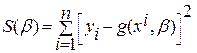(1.2)
приймає мінімальне значення по b ÎRm, де Rm – m-вимірний евклідів простір.
Зауважимо, що сам принцип найменших квадратів в явному вигляді був сформульований ще у 18-му сторіччі видатними математиками Гауссом та Лежандром. Термін “регресійний аналіз” з’явився значно пізніше, вже у другій половині XIX сторіччя. Його пов’язують з роботами видатного англійського вченого Ф.Гальтона, який, зокрема, застосовував МНК в своїх антропологічних дослідженнях. При цьому Ф.Гальтон спостерігав деякі ознаки виродження, тобто регресу, певних розмірних людських ознак, так що в даних дослідженнях термін “регресія” був цілком виправданим. Роботи, про які йде мова, стали відомими, методика роботи автора з експериментальними даними була використана іншими дослідниками, і при цьому термін “регресія” автоматично зберігся і став вживатися без будь-яких обмежень на область досліджень та на характер закономірностей, що в цих дослідженнях виявляються.
На даний час розроблено багато ефективних обчислювальних алгоритмів для знаходження розв’язку задачі мінімізації виразу (1.2). На основі таких алгоритмів працюють відповідні комп’ютерні програми сучасного математичного забезпечення. Зауважимо, що у багатьох важливих випадках розв’язок зазначеної задачі можна одержати у явному вигляді.
3. – 5. Розв’язок цих задач одержується на основі припущень щодо ймовірнісної поведінки величини e – випадкової складової регресійної моделі. Найбільш фундаментальні результати у цьому напрямку на даний час одержано для випадку, коли зазначена випадкова складова має нормальний розподіл ймовірностей. Деякі з цих результатів будуть наведені в подальшому.
РОЗДІЛ 2
ПРОСТА ЛІНІЙНА РЕГРЕСІЯ