Найти методом точного поиска хроматическое число графа

Решение:

Перейдём от орграфа к неографу и построим для его матрицу смежности R:

R=

Так как матрица симметрична относительно главной диагонали, то выражение для определения всех внутренне устойчивых множеств можно находить для половины матрицы. Найдем по методу Магу все F_i , которые содержат вершины, не принадлежащие максимальным внутренне устойчивым множествам S_i. Запишем:

(1Ú2467)(2Ú3456)(3Ú456)(4Ú56)(5Ú678)(6Ú7)=(12Ú13456Ú2467Ú234567)(34Ú

Ú356Ú456Ú456)(56Ú57Ú678Ú678)=(1234Ú12356Ú12456Ú13456Ú13456Ú

Ú13456Ú23467Ú234567Ú24567)(56Ú57Ú678)=123456Ú123457Ú1234678Ú

Ú12356Ú123567Ú1235678Ú12456Ú124567Ú1245678Ú13456Ú134567Ú

Ú1345678Ú234567Ú234567Ú234678Ú24567Ú24567Ú245678=123457Ú

Ú12356Ú12456Ú13456Ú234678Ú24567

F₁={x₁,x₂,x₃,x₄,x₅,x₇}, F₂={x₁,x₂,x₃,x₅,x₆}, F₃={x₁,x₂,x₄,x₅,x₆}, F₄={x₁,x₃,x₄,x₅,x₆}, F₅={x₂,x₃,x₄,x₆,x₇,x₈}, F₆={x₂,x₄,x₅,x₆,x₇}.

			F5, F6
	F4
	F3, F6
Вершины xi		Ï	F2
	F5
			F1
	F2,Ф3,Ф4
	F1, F2, Ф3, Ф4, Ф6

Для "вершины запишем выражение y_jÚy_kÚ…y_n=1 и найдем конъюнкцию этих всех выражений: (цифра это y_i)

1245(5Ú6)(3Ú6)(2Ú3Ú4)(1Ú2Ú3Ú4Ú6)=1245(53Ú6)(2Ú3Ú4)=1245(532Ú53Ú345Ú

Ú62Ú63Ú46)=12345Ú12456Ú123456Ú12456=12345Ú12456

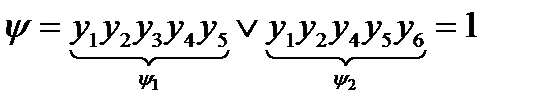
Выбираем любое Y_i , которое содержит минимальное число букв:

Y₁={ y₁y₂y₃y₄y₅ } содержит 5 букв Þ хроматическое число g(G)=5.

Далее запишем для раскраски графа следующее:

y₁ ® F₁={x₁, x₂,x₃,x₄,x₅,x₇}ÞS₁={x₆, x₈} —

эти вершины окрашиваем в цвет “1”

y₂ ® F₂={x₁,x₂,x₃,x₅,x₆}ÞS₂={x₄, x_7, x₈} Þ{x₄,x₇} —

эту вершину окрашиваем в цвет “2”

y₃ ® F₃={x₁,x₂,x₄,x₅,x₆}ÞS₃={x₃, x_7, x₈} Þ{x₃} —

эти вершины окрашиваем в цвет “3”

y₄ ® F₄={x₁,x₃,x₄,x₅,x₆}ÞS₄={x₂, x₇, x₈} Þ{x₂} —

эту вершину окрашиваем в цвет “4”

y₅ ® F₅={x₂,x₃,x₄,x₆,x₇,x₈}ÞS₅={x₁, x₅} —

эти вершины окрашиваем в цвет “5”

X3

X1

X2

X5

X6

X7

X8

u RYEmNRjjgN1ISQo7yTr814wDldB6N9w9TEIp0+GAKzVExzQOHQyJfWfx+o/N3E3s42MqSwf+N8lD RqpsdBiSldDGdbzcrX6kgnfxBwa6uSMFV6bapWUnauBSE3P9r4pf4bae0o9/f/EbAAD//wMAUEsD BBQABgAIAAAAIQDvUdyx3wAAAAoBAAAPAAAAZHJzL2Rvd25yZXYueG1sTI/RToNAEEXfTfyHzZj4 0tiFNqAgS2NM/QCLmvg2sCuQsrOE3VLq1zs+6eNkTu49t9gtdhCzmXzvSEG8jkAYapzuqVXwVr3c PYDwAUnj4MgouBgPu/L6qsBcuzO9mvkQWsEh5HNU0IUw5lL6pjMW/dqNhvj35SaLgc+plXrCM4fb QW6iKJUWe+KGDkfz3JnmeDhZBR/vWfUtB6xXfv/ZptVqf5mzo1K3N8vTI4hglvAHw68+q0PJTrU7 kfZiUJDGmy2jCpKEJzBwv41jEDWTSRaBLAv5f0L5AwAA//8DAFBLAQItABQABgAIAAAAIQC2gziS /gAAAOEBAAATAAAAAAAAAAAAAAAAAAAAAABbQ29udGVudF9UeXBlc10ueG1sUEsBAi0AFAAGAAgA AAAhADj9If/WAAAAlAEAAAsAAAAAAAAAAAAAAAAALwEAAF9yZWxzLy5yZWxzUEsBAi0AFAAGAAgA AAAhAAemgIcXAgAAQwQAAA4AAAAAAAAAAAAAAAAALgIAAGRycy9lMm9Eb2MueG1sUEsBAi0AFAAG AAgAAAAhAO9R3LHfAAAACgEAAA8AAAAAAAAAAAAAAAAAcQQAAGRycy9kb3ducmV2LnhtbFBLBQYA AAAABAAEAPMAAAB9BQAAAAA= " strokecolor="black [3213]" strokeweight="1.5pt"/> E W1GgSQ3GOGI/VJLCVrIe/y3jQCY03493D5NQynTY40oN0TGNQwdj4tBZvP9DM3cTh/iYytKJ/03y mJEqGx3GZCW0cT0vd6sfqOB9/J6Bfu5IwaWpt2ndiRq41cTc8K/iZ7itp/TD75//BgAA//8DAFBL AwQUAAYACAAAACEApE8uxuEAAAAKAQAADwAAAGRycy9kb3ducmV2LnhtbEyPy07DMBBF90j8gzVI bCpqh5S2CXEqhMoH0AASu0lskqh+RLGbpnw9wwqWM3N059xiN1vDJj2G3jsJyVIA067xqnethLfq 5W4LLER0Co13WsJFB9iV11cF5sqf3aueDrFlFOJCjhK6GIec89B02mJY+kE7un350WKkcWy5GvFM 4dbweyHW3GLv6EOHg37udHM8nKyEj/es+uYG60XYf7brarG/TNlRytub+ekRWNRz/IPhV5/UoSSn 2p+cCsxISEWaESph9bACRsAmTRJgNS3EZgu8LPj/CuUPAAAA//8DAFBLAQItABQABgAIAAAAIQC2 gziS/gAAAOEBAAATAAAAAAAAAAAAAAAAAAAAAABbQ29udGVudF9UeXBlc10ueG1sUEsBAi0AFAAG AAgAAAAhADj9If/WAAAAlAEAAAsAAAAAAAAAAAAAAAAALwEAAF9yZWxzLy5yZWxzUEsBAi0AFAAG AAgAAAAhAA7VW4IYAgAARQQAAA4AAAAAAAAAAAAAAAAALgIAAGRycy9lMm9Eb2MueG1sUEsBAi0A FAAGAAgAAAAhAKRPLsbhAAAACgEAAA8AAAAAAAAAAAAAAAAAcgQAAGRycy9kb3ducmV2LnhtbFBL BQYAAAAABAAEAPMAAACABQAAAAA= " strokecolor="black [3213]" strokeweight="1.5pt"/> 3 okATCoxhwmGmKPmdoAP+a8qAS+h9mO4BJiaEKn/AFQqiQxqDDqbEsbNw/sdm7ieO8SGVxgv/m+Qp I1bWyk/JkittB17uVz9SwYb4AwPD3IGCa13v4rYjNXCqkbnxW4W/cFeP6cfPv/wNAAD//wMAUEsD BBQABgAIAAAAIQB9KwRv3wAAAAoBAAAPAAAAZHJzL2Rvd25yZXYueG1sTI/RToNAEEXfTfyHzZj4 0tgFSbEgS2NM/QCLmvg2sCuQsrOE3VLq1zs+6eNkTu49t9gtdhCzmXzvSEG8jkAYapzuqVXwVr3c bUH4gKRxcGQUXIyHXXl9VWCu3ZlezXwIreAQ8jkq6EIYcyl90xmLfu1GQ/z7cpPFwOfUSj3hmcPt IO+jKJUWe+KGDkfz3JnmeDhZBR/vWfUtB6xXfv/ZptVqf5mzo1K3N8vTI4hglvAHw68+q0PJTrU7 kfZiUJBEScaogs2GJzDwkMQxiJrJdJuCLAv5f0L5AwAA//8DAFBLAQItABQABgAIAAAAIQC2gziS /gAAAOEBAAATAAAAAAAAAAAAAAAAAAAAAABbQ29udGVudF9UeXBlc10ueG1sUEsBAi0AFAAGAAgA AAAhADj9If/WAAAAlAEAAAsAAAAAAAAAAAAAAAAALwEAAF9yZWxzLy5yZWxzUEsBAi0AFAAGAAgA AAAhAHobQ+kXAgAARAQAAA4AAAAAAAAAAAAAAAAALgIAAGRycy9lMm9Eb2MueG1sUEsBAi0AFAAG AAgAAAAhAH0rBG/fAAAACgEAAA8AAAAAAAAAAAAAAAAAcQQAAGRycy9kb3ducmV2LnhtbFBLBQYA AAAABAAEAPMAAAB9BQAAAAA= " strokecolor="black [3213]" strokeweight="1.5pt"/>

X4

Задание №3

Решить задачу коммивояжера для данной матрицы расстояний.

(Задача коммивояжера:

Коммивояжер должен выехать из заданного города, объехать все остальные города и вернуться назад по кратчайшему маршруту.)

	*
		*
			*
				*
					*
						*
							*
								*

Решение:

В клетку с индексом ii ставим символ *.Затем с помощью процедуры редукции сначала производим приведение матрицы по строкам, а потом — по столбцам.

*

*

*

*

*

*

*

*

å=97

*

*

*

*

*

*

Все маршруты, найденные в ходе решения, больше либо равны 111

*

*

å=111

Нулевая клетка	Число вычитаемое из	å
строки	столбца
(1,6)
(1,8)
(2,7)
(3,2)
(4,1)				Þ4®1
(5,2)				Из города 4 едет в 1
(6,2)
(7,4)
(7,5)
(7,8)
(8,3)

Вычеркиваем строку 4 и столбец 1, а в клетку (1,4) ставим символ *.

			*
	*
		*
				*
					*
						*
							*

å=111

Так как данную матрицу привести невозможно, строим таблицу нулевых клеток.

Нулевая клетка	Число вычитаемое из	å
строки	столбца
(1,6)
(1,8)
(2,7)
(3,2)				Из города 2 едет в 7
(5,2)				Þ2®7 , 4®1
(6,2)
(7,4)
(7,5)
(7,8)
(8,3)

Вычеркиваем строку 2 и столбец 7, а в клетку (7,2) ставим символ *.

			*
		*
				*
					*
	*
						*

å=111

Так как данную матрицу привести невозможно, строим таблицу нулевых клеток.

Нулевая клетка	Число вычитаемое из	å
строки	столбца
(1,6)
(1,8)
(3,2)				Из города 6 едет в 2
(5,2)				Þ6®2®7 , 4®1
(6,2)
(7,4)
(7,5)
(7,8)
(8,3)

Вычеркиваем строку 6 и столбец 2, а в клетку (7,6) ставим символ *(избегаем зацикливания 6®2®7).

		*
	*
			*
				*
					*

Производим приведение матрицы по строкам.

		*
	*
			*
				*
					*
							å=119

Так как данную матрицу привести по столбцам невозможно, строим таблицу нулевых клеток.

Нулевая клетка	Число вычитаемое из	å
строки	столбца
(1,6)
(1,8)
(3,4)				Из города 5 едет в 3
(5,3)				Þ6®2®7 , 4®1,
(7,4)				5®3
(7,5)
(7,8)
(8,3)

Вычеркиваем строку 5 и столбец 3, а в клетку (3,5) ставим символ *.

	*
		*
			*
				*

Производим приведение матрицы по строкам.

	*
		*
			*
				*
						å=121

Так как данную матрицу привести по столбцам невозможно, строим таблицу нулевых клеток.

Нулевая клетка	Число вычитаемое из	å
строки	столбца
(1,6)
(1,8)
(3,4)				Из города 7 едет в 5
(7,4)				Þ6®2®7®5®3 , 4®1,
(7,5)
(7,8)
(8,6)

Вычеркиваем строку 7 и столбец 5, а в клетку (3,6) ставим символ *(избегаем зацикливания 6®2®7®5®3).

	*
		*
			*

å=121

Так как данную матрицу привести невозможно, строим таблицу нулевых клеток.

Нулевая клетка	Число вычитаемое из	å
строки	столбца
(1,6)
(1,8)				Из города 7 едет в 5
(3,4)				Þ6®2®7®5®3®
(8,6)				®4®1,

Вычеркиваем строку 3 и столбец 4, а в клетку (1,6) ставим символ *(избегаем зацикливания 6®2®7®5®3®4®1).

	*
		*

Кратчайший маршрут коммивояжера (121):

Путь: 10+8+18+18+15+16+9+27=121