Каноническое уравнение эллипса
УСЛОВИЕ ПЕРЕСЕЧЕНИЯ ДВУХ ПРЯМЫХ
Непараллельные прямые 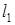 и
и 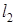 пересекаются тогда и только тогда, когда расстояние
пересекаются тогда и только тогда, когда расстояние 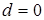 , что равносильно равенству
, что равносильно равенству 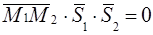 или
или
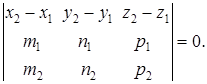
Замечание. Это же условие имеет место, если прямые параллельны, так как из 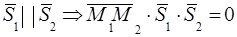 .
.
ПРЯМАЯ И ПЛОСКОСТЬ В ПРОСТРАНСТВЕ
ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ
Пусть заданы прямая линия 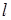 и плоскость
и плоскость 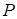 :
:
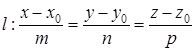 ;
;
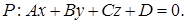
УГОЛ МЕЖДУ ПРЯМОЙ И ПЛОСКОСТЬЮ
Углом 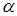 между прямой
между прямой 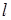 и плоскостью
и плоскостью 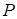 называется угол между прямой и проекцией этой прямой на плоскость (рис. 42).
называется угол между прямой и проекцией этой прямой на плоскость (рис. 42).
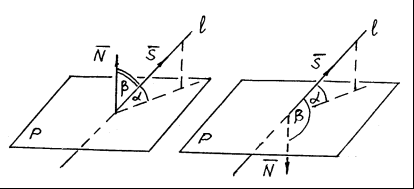 Рис. 42 Рис. 42 |
Этот угол и угол 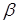 между нормальным вектором
между нормальным вектором 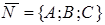 плоскости
плоскости 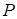 и направляющим вектором
и направляющим вектором 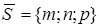 прямой
прямой 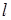 связаны соотношением
связаны соотношением 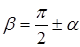 (рис. 42)
(рис. 42)
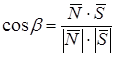 ’
’
но 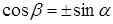 , откуда
, откуда
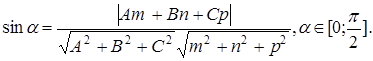
УСЛОВИЕ ПЕРПЕНДИКУЛЯРНОСТИ ПРЯМОЙ И ПЛОСКОСТИ
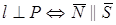 или
или 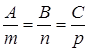 .
.
УСЛОВИЕ ПАРАЛЛЕЛЬНОСТИ ПРЯМОЙ И ПЛОСКОСТИ
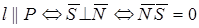 или
или 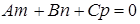 .
.
ПЕРЕСЕЧЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ
Пусть даны прямая 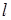 и плоскость
и плоскость 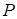 :
:
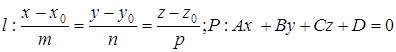 ,
,
причем 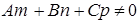 , т.е.
, т.е. 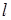 не параллельна
не параллельна 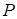 .
.
Для определения координат точки пересечения прямой и плоскости следует решить систему уравнений, определяющих прямую 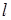 и плоскость
и плоскость 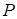 . Решение этой системы упрощается, если уравнения прямой представить в параметрической форме:
. Решение этой системы упрощается, если уравнения прямой представить в параметрической форме:
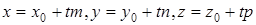 .
.
Параметр 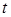 подбираем так, чтобы координаты точки, принадлежащей прямой, удовлетворяли уравнению плоскости:
подбираем так, чтобы координаты точки, принадлежащей прямой, удовлетворяли уравнению плоскости:
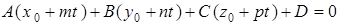 ,
,
откуда
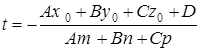 .
.
Найденное значение 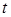 подставляем в параметрические уравнения прямой и получим координаты точки, одновременно принадлежащей прямой и плоскости.
подставляем в параметрические уравнения прямой и получим координаты точки, одновременно принадлежащей прямой и плоскости.
Замечание. При формальном решении данной задачи значение параметра 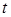 из формулы не определяется при
из формулы не определяется при 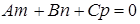 т.е. когда прямая и плоскость параллельны. Если дополнительно к этому условию имеет место равенство
т.е. когда прямая и плоскость параллельны. Если дополнительно к этому условию имеет место равенство 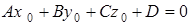 , то эти два условия означают, что
, то эти два условия означают, что 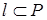 .
.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Выведите формулу для вычисления угла между прямой и плоскостью.
2. Запишите условие ортогональности прямой и плоскости.
3. При выполнении каких условий прямая принадлежит плоскости?
ПУЧОК ПЛОСКОСТЕЙ
Пучком плоскостей называется совокупность всех плоскостей, проходящих через одну и ту же прямую. Эта прямая называется осью пучка.
Уравнением пучка называется уравнение, из которого можно получить уравнение любой плоскости, принадлежащей этому пучку.
Если 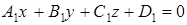 и
и 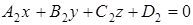 – две различные плоскости пучка, то уравнение
– две различные плоскости пучка, то уравнение 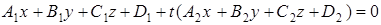 , где
, где 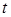 - параметр, будет уравнением пучка. Осью пучка будет прямая
- параметр, будет уравнением пучка. Осью пучка будет прямая
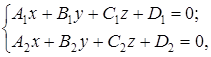
параметр 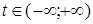 . Это утверждение доказывается так же, как для уравнения пучка прямых на плоскости.
. Это утверждение доказывается так же, как для уравнения пучка прямых на плоскости.
§17. ЛИНИИ ВТОРОГО ПОРЯДКА НА ПЛОСКОСТИ
Алгебраическое уравнение второго порядка имеет вид
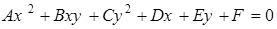 ,
,
где коэффициенты 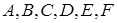 - какие угодно постоянные с одним ограничением:
- какие угодно постоянные с одним ограничением: 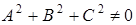 .
.
ОКРУЖНОСТЬ
Определение. Окружностью называется геометрическое место точек плоскости, равноудаленных от данной точки 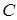 этой плоскости.
этой плоскости.
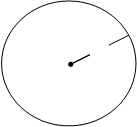 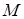 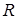 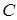 Рис. 43 Рис. 43 |
Точка 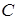 называется центром окружности, расстояние от центра до любой точки окружности называется ее радиусом.
называется центром окружности, расстояние от центра до любой точки окружности называется ее радиусом.
Пусть на плоскости, где задана декартова прямоугольная система координат, точка 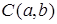 - центр окружности, постоянная
- центр окружности, постоянная 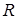 - ее радиус. Если
- ее радиус. Если 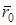 - радиус-вектор точки
- радиус-вектор точки 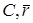 - радиус-вектор точки
- радиус-вектор точки 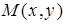 , то точка
, то точка 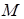 принадлежит окружности тогда и только тогда, когда (рис. 43)
принадлежит окружности тогда и только тогда, когда (рис. 43) 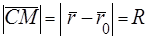 . Полученное равенство есть векторное уравнение окружности радиуса
. Полученное равенство есть векторное уравнение окружности радиуса 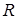 и с центром в точке
и с центром в точке 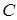 . В координатной форме это уравнение имеет вид
. В координатной форме это уравнение имеет вид 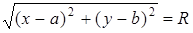 или
или 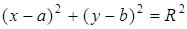 . Последнее уравнение называется нормальным уравнением окружности с центром в точке
. Последнее уравнение называется нормальным уравнением окружности с центром в точке 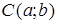 и радиусом
и радиусом 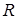 .
.
Замечания. 1. Если 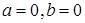 , то получим уравнение окружности с центром в начале координат:
, то получим уравнение окружности с центром в начале координат: 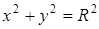 ;
;
2. Окружность - линия второго порядка: из 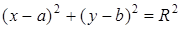 имеем
имеем 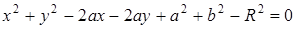 .
.
3. Если в уравнении второго порядка коэффициенты при 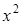 и
и 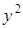 равны, а произведение
равны, а произведение 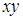 отсутствует, то такое уравнение определяет либо окружность, либо точку, либо ничего:
отсутствует, то такое уравнение определяет либо окружность, либо точку, либо ничего: 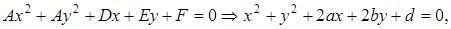 где
где 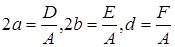 .
.
Выделяя полные квадраты, уравнение преобразуем к виду 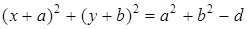 .
.
Если 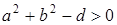 , то это - уравнение окружности с центром в точке
, то это - уравнение окружности с центром в точке 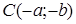 радиуса
радиуса 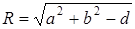 , если
, если 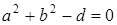 , то это - уравнение точки
, то это - уравнение точки 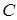 , если
, если 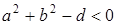 , то нет такой точки, координаты которой удовлетворяли бы этому уравнению.
, то нет такой точки, координаты которой удовлетворяли бы этому уравнению.
К линиям второго порядка относятся эллипс, гипербола, парабола, которые представляют собой линии пересечения кругового конуса плоскостями, не проходящими через его вершину.
Рассмотрим вывод канонических уравнений этих кривых, основанный на их фокальных свойствах.
КАНОНИЧЕСКОЕ УРАВНЕНИЕ ЭЛЛИПСА
Определение. Эллипсом называется геометрическое место точек плоскости, для которых сумма расстояний до двух данных точек 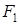 и
и 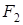 этой плоскости есть величина постоянная.
этой плоскости есть величина постоянная.
Точки 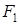 и
и 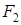 называются фокусами эллипса.
называются фокусами эллипса.
Пусть на плоскости заданы точки 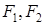 , расстояние между которыми равно
, расстояние между которыми равно 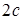 , и постоянная
, и постоянная 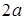 . Если обозначить расстояние от точки
. Если обозначить расстояние от точки 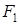 до точки
до точки 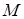 через
через 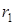 , а от точки
, а от точки 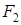 до точки
до точки 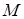 через
через 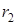 , то точка
, то точка 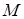 по определению принадлежит эллипсу тогда и только тогда, когда
по определению принадлежит эллипсу тогда и только тогда, когда 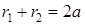 .
.
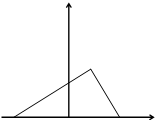 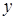 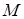 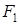 0 0 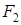  Рис. 44 Рис. 44 |
Для вывода канонического уравнения эллипса начало 0 декартовой прямоугольной системы координат выберем в середине отрезка 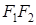 , а оси Ox и Oy направим так, как на рис. 44. В этом случае имеем
, а оси Ox и Oy направим так, как на рис. 44. В этом случае имеем 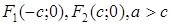 (из
(из 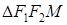 следует
следует 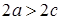 ) и
) и
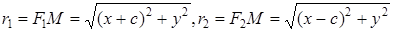 , где
, где 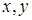 - координаты точки
- координаты точки 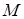 . Уравнение, которому удовлетворяют координаты точки, принадлежащей эллипсу, будет иметь вид
. Уравнение, которому удовлетворяют координаты точки, принадлежащей эллипсу, будет иметь вид 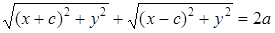 .
.
Полученное уравнение эллипса можно упростить, дважды возведя обе части уравнения в квадрат: 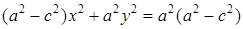 или
или 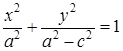 .
.
Последнее уравнение является не только следствием уравнения эллипса, но и эквивалентно ему. Действительно, если координаты точки 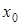 ,
, 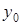 удовлетворяют последнему уравнению, то
удовлетворяют последнему уравнению, то 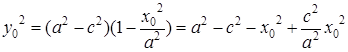 .
.
Подставим это значение 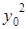 и
и 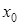 в выражения для
в выражения для 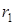 и
и 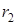 :
:
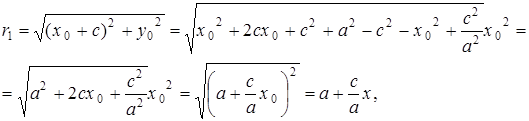
так как 
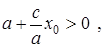 (
( 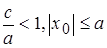 из последнего уравнения). Аналогично получаем, что
из последнего уравнения). Аналогично получаем, что 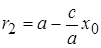 , и окончательно имеем
, и окончательно имеем 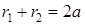 .
.
Таким образом, точка, координаты которой удовлетворяют уравнению 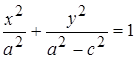 , принадлежат эллипсу.
, принадлежат эллипсу.
Если ввести обозначение 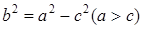 , то окончательно получим каноническое уравнение эллипса:
, то окончательно получим каноническое уравнение эллипса:
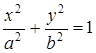 .
.
