Теорема. Дисперсия равна среднему квадратов значений признака минус квадрат общей средней

Несмещенной оценкой генеральной дисперсии служит исправленная выборочная дисперсия:

.

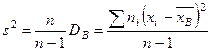Кроме дисперсии, для характеристики рассеяния значений признака генеральной совокупности вокруг своего среднего значения пользуются сводной характеристикой – средним квадратическим отклонением.

Выборочным средним квадратическим отклонением (стандартом)называют квадратный корень из выброчной дисперсии:

.

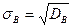Генеральным средним квадратическим отклонением (стандартом)называют квадратный корень из генеральной дисперсии:

.

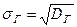Оценка характеристик положения

Наиболее распространенными опенками характеристик положения являются среднее арифметическое выборки (выборочное среднее), выборочная медиана и выборочная мода. В дальнейшем будем, опускать термин «выборочная», имея, однако, в виду, что любая оценка, начисляемая по выборке, является всего лишь приближенным значением соответствующей характеристики генеральной совокупности

В качестве меры относительного разброса данных используют коэффициент вариации

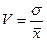или

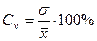
Величину отклонения выборочного показателя (статистики) от его генерального пара­метра называют статистической ошибкой. Для измерения этой ошибки некоторой статистики квадратичная (стандартная) ошибка статистики (нельзя путать со средним квадратичным от­клонением изучаемой случайной переменной). Так, стандартная ошибка среднего арифметиче­ского может быть найдена по формуле:

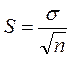
Доверительный интервал

По известным точечным выборочным характеристикам можно построить интервальную оценку или доверительный интервал, в котором с той или иной вероятностью находится генеральный параметр. Вероятности, признанные достаточными для уверенного суждения о гене­ральных параметрах на основании известных выборочных показателей, называют доверитель­ными. Обычно в медико-биологических исследованиях приемлемым является значение довери­тельной вероятности Р=0,05 (95%). При этом вероятность выхода истинного значения парамет­ра за пределы этих границ не превышает 1-0,95=0,05 (5%). Величину, дополняющую довери­тельную вероятность да единицы, обычно обозначают α.

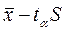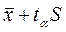Как известно из центральной предельной теоремы, независимо от распределения исход­ной совокупности, из которой извлечены выборки, выборочные средние имеют приближенно нормальное распределение. Таким образом, доверительный интервал для выборочного среднего значения находится между границами и , где 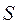- стандартная ошибка среднего, 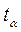- коэффициент Стьюдента, величина, зависящая от объема выборки 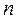(или соответствующего числа степеней свободы 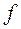) и выбранного уровня доверительной вероятности, определяется по таблицам распределений Стьюдента. Величина коэффициента 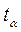, определяется по таблице на уровне α, дополняющем доверительную вероятность до 1,т.е. в случае 95% доверительного ин­тервала на уровне (1 -0,95) = 0,05 с учетом симметрии интервала.

Вариационный ряд — числовые значения признака, представленные в ранговом порядке с соответствующими этим значениям частотами.

Основные обозначения вариационного ряда:

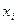- варианта, отдельное числовое выражение изучаемого признака;

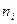- частота (“вес”) варианты, число ее повторений в вариационном ряду;

n — общее число наблюдений (т.е. сумма всех частот, n=Σ );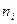

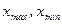- крайние варианты, ограничивающие вариационный ряд (лимиты ряда);

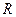- амплитуда ряда (т.е. разность между максимальной и минимальной вариантами, ).

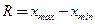Виды вариационных рядов:

а) простой — ряд, в котором каждая варианта встречается по одному разу (р=1);

б)взвешенный — ряд, в котором отдельные варианты встречаются неоднократно и с разной частотой.

Назначение вариационного ряда

Вариационный ряд используется для определения средней величины ( 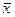) и критериев разнообразия признака, подлежащего изучению ( ).

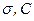Средняя величина - обобщающая характеристика размера изучаемого признака. Она позволяет одним числом количественно охарактеризовать качественно однородную совокупность.

Применение средних величин:

а) для оценки состояния здоровья - например, параметров физического развития (средний рост, средний вес, средний объем жизненной емкости легких и др.), соматических показателей (средний уровень сахара в крови, средний пульс, средняя СОЭ и др.);

б) для оценки организации работы лечебно-профилактических и санитарно-противоэпидемических учреждений, а также деятельности отдельных врачей и других медицинских работников (средняя длительность пребывания больного на койке, среднее число посещений на 1 ч приема в поликлинике и др.);

в) для оценки состояния окружающей среды.

Среднеквадратическое отклонение - мера колеблемости (вариабельности) вариационного ряда. Сигма - величина именованная, т.е. выражается в тех же единицах, что и варианты ряда.

Применение среднеквадратического отклонения:

а) для суждения о колеблемости вариационных рядов и сравнительной оценки типичности (представительности) средних арифметических величин. Это необходимо в дифференциальной диагностике при определении устойчивости признаков;

б) для реконструкции вариационного ряда, т.е. восстановления его частотной характеристики на основе правила «трех сигм». В интервале М±3σ находится 99,7% всех вариант ряда, в интервале М±2σ— 95,5% и в интервале М±1σ— 68,3% вариант ряда;

в) для выявления «выскакивающих» вариант (при сопоставлении реального и реконструированного вариационных рядов);

г) для определения параметров нормы и патологии с помощью сигмальных оценок;

д) для расчета коэффициента вариации;

е) для расчета средней ошибки средней арифметической величины.

Коэффициент вариации (C) - процентное отношение среднеквадратического отклонения к среднеарифметической величине:

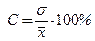
Коэффициент вариации - это относительная мера колеблемости вариационного ряда.

Применение коэффициента вариации

а) для оценки разнообразия каждого конкретного вариационного ряда и, соответственно, суждения о типичности отдельной средней (т.е. ее способности быть полноценной обобщающей характеристикой данного ряда). При С<10% разнообразие ряда считается слабым, при С от 10% до 20% - средним, а при С>20% - сильным. Сильное разнообразие ряда свидетельствует о малой представительности (типичности) соответствующей средней величины и, следовательно, о нецелесообразности ее использования в практических целях.

б) для сравнительной оценки разнообразия (колеблемости) разноименных вариационных рядов и выявления более-менее стабильных признаков, что имеет значение в дифференциальной диагностике.

ЗАДАЧА-ЭТАЛОН

Условие задачи. В городе N в 2000 г. проведено измерение массы тела 7-летних мальчиков. По данным аналогичного исследования, выполненного в городе N в 1990 г., средняя масса тела 7-летних мальчиков составила 23,8 кг, σ± 3,6 кг.

Задание.1. Вычислить среднюю арифметическую величину ( 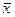) и критерии разнообразия вариационного ряда (σ, С).

2. Оценить полученные результаты, сравнить их с данными предыдущего исследования, сделать соответствующие выводы.

РЕШЕНИЕ ЗАДАЧИ