Измерительная установка и методика измерений

Установка № 1

Приборы и оборудование: лабораторная установка, в которую вмонтированы миллиамперметр, милливольтметр, трансформатор, диодный мостик, потенциометры, переключатель, электромагнит, контакты и полупроводниковый образец.

Сущность метода измерения холловской разности потенциалов заключается в следующем. Напряжение от сети через понижающий трансформатор Т1 подается на диодный мостик YD1. Выпрямленное напряжение с помощью потенциометра R1 через переключатель SA2 подается на электромагнит ЭМ. Направление магнитного поля в образце О изменяется переключателем SA2, а ток через магнит измеряется миллиамперметром РА1. Ток через образец О регулируется потенциометром R2 и измеряется миллиамперметром РА2. Холловская разность потенциалов измеряется милливольтметром PV1 (см. рис.15.2).

Порядок выполнения работы

1. Изучите краткую теорию и принцип действия установки и определите цену деления используемых приборов.

2. Включите установку в сеть. Установите переключатель SA1 в верхнее положение и потенциометром R2 установите через образец ток 0.1 mA. Для этого тока потенциометром R1 установите три значения тока через электромагнит в пределах от 130 до 160 mA. Для каждого значения тока через электромагнит измерьте холловскую разность потенциалов U^– и U⁺, изменяя направление тока через электромагнит переключателем SA2. Проделайте такие же измерения для токов через образец 0.2 mA и 0.3 mA. Результаты измерений занесите в таблицу 15.1.

Рис.15.2. Электрическая схема установки

Замечание:Контакты А и С (рис.15.1) подключения милливольтметра, как правило, находятся несимметрично (не находятся на эквипотенциальной поверхности в отсутствие магнитного поля). Поэтому измеряемая разность потенциалов U на самом деле является суммой Холловской разности потенциалов U_х и разности потенциалов Dj, возникшей вследствие несимметричности контактов: U⁺=U_х+Dj. При изменении направления магнитного поля на противоположное изменится на противоположное и направление силы Лоренца, а значит, изменится знак Холловской разности потенциалов, но знак Dj останется без изменения. Полная разность потенциалов будет: U^–=–U_х+Dj. Окончательно получим формулу для Холловской разности потенциалов, исключающей влияние несимметричности контактов А и С:

U_х=(U⁺ – U^–)/2. (15.9)

3. По формуле (15.9) вычислите Холловскую разность потенциалов для каждого измерения. Результаты занесите в таблицу 15.1.

4. По графику (рис.15.3) зависимости В от I_эм определите В и занесите в таблицу 15.1.

5. По формуле (15.6) рассчитайте R_Х для каждого значения В, определяемого по току через электромагнит. Вычислите среднее значение R_Х, по которому определите концентрацию носителей заряда n, используя формулу (15.5).

6. Зная R и g, по формуле (15.8) вычислите подвижность носителей заряда u.

7. Вычислите погрешность R_Х .

8. Все полученные результаты запишите в таблицу 15.1.

4.00   3.00   2.00   1.00

Таблица 15.1

Ток через образец I, мA	Ток через электро- магнит Iэм., мA	U+, мB	U–, мB	Uх, мB	B, Тл	RХ, м3/Кл	RХ ср, м3/Кл	ΔRХ	u, м2/(В.с)	n, м-3
0.1
0.2
0.3

Установка № 2

Приборы и оборудование: измерительный блок и объект исследования.

Рис.15.4. Внешний вид установки.

Измерительный блок формирует и регулирует силу тока электромагнита I_эм и преобразователя (ток через образец) I, изменяет полярность тока. Ток преобразователя и электромагнита изменяются в пределах соответственно 0÷5 мА и 0÷10 мА. Объект исследования состоит из полупроводникового преобразователя Холла и электромагнита.

Порядок выполнения работы

1. Включить установку (переключатель «сеть» находится на задней панели измерительного блока).

2. Переключателем измерителя переключить миллиамперметр в режим измерения тока через датчик Холла (при этом должен загореться соответствующий светодиод).

3. Установить полярность «+» переключателем «направление тока» (в индикации миллиамперметра отсутствует знак «–»).

4. Кнопками регулировки силы тока «+» и «–» установить силу тока через датчик Холла I=3 мА.

5. Переключателем измерителя переключить миллиамперметр в режим измерения тока электромагнита (при этом должен загореться соответствующий светодиод).

6. Установить полярность «+» переключателем «направление тока» (в индикации миллиамперметра отсутствует знак «–»).

7. Кнопками регулировки силы тока «+» и «–» установить силу тока электромагнита I_эм=3 мА.

8. Измерить ЭДС Холла U⁺, записать все величины в таблицу 15.2.

9. Кнопками регулировки силы тока «+» и «–» устанавливать силу тока электромагнита I_эм=4 мА; 5 мА; … 10 мА, каждый раз измеряяи записывая величину U⁺.

10. Установить полярность «–» переключателем «направление тока» (в индикации миллиамперметра присутствует знак «–»).

11. Повторить пункты 7-9, записывая в таблицу ЭДС Холла U^– при другом направлении магнитного поля.

12. Повторить измерения ЭДС Холла для тока через датчик I=4 мА (пункты 2-11), а затем для I=5 мА.

13. По формуле (15.9) вычислите Холловскую разность потенциалов для каждого измерения. Результаты занесите в таблицу 15.2.

U_х=(U⁺ – U^–)/2. (15.9)

14. По графику (рис.15.5) зависимости В от I_эм определите В и занесите в таблицу 15.2.

15. По формуле (15.6) рассчитайте R_Х для каждого значения В, определяемого по току через электромагнит.

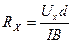, (15.6)

где I – ток через образец, d=3^.10^-4м – толщина пластинки.

16. Вычислите среднее значение R_Х, по которому определите концентрацию носителей заряда n, используя формулу (15.5):

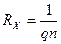. (15.5)

17. Зная R и g, по формуле (15.8) вычислите подвижность носителей заряда u:

u=g/(en)=gR_Х. (15.8)

18. Вычислите погрешности R_Х и u.

Таблица 15.2

Ток через образец I, мA	Ток через электро- магнит Iэм., мA	U+, мB	U–, мB	Uх, мB	B, Тл	RХ, м3/Кл	RХ ср, м3/Кл	ΔRХ	u, м2/(В.с)	Δ u

Контрольные вопросы

1. В чем заключается эффект Холла?

2. Чем объясняется эффект Холла?

3. Чему равна и как направлена сила Лоренца?

4. Для каких целей практически используется эффект Холла?

5. Выведите формулу для Холловской разности потенциалов.

6. Как расположены эквипотенциальные поверхности при прохождении постоянного тока через образец: а) в отсутствие магнитного поля; в) при включенном магнитном поле?

7. Как исключается погрешность, связанная с несимметричностью контактов подключения миллиамперметра к образцу?

8. Каков знак носителей тока в изучаемом образце?

Используемая литература

[1] §§ 21.2, 23.2;

[2] §§ 14.2, 14.5;

[4] т.2, §§ 79;

[5] §§ 114, 117.

Лабораторная работа 2-16

Изучение гистерезиса ферромагнитных материалов (ФПЭ-07)

Цель работы – изучение гистерезиса ферромагнитных материалов, расчет и графическое построение основной кривой намагничивания, расчет работы перемагничивания и коэрцитивной силы.

Теоретическое введение

Все вещества обладают магнитными свойствами, т.е. являются магнетиками. По своим магнитным свойствам магнетики делятся на три основные группы: диамагнетики, парамагнетики и ферромагнетики. Всякая среда при внесении её в иагнитное поле намагничивается в той или иной степени, то есть создаёт своё собственное магнитное поле, накладывающееся на внешнее поле.

Количественной характеристикой намагниченного состояния вещества служит векторная величина – намагниченность , равная магнитному моменту единицы объема магнетика:

, (16.1)

где ∆V – малый объем магнетика; – сумма магнитных моментов всех атомов в объеме ∆V. Намагниченность связана с напряженностью магнитного поля:

, (16.2)

где χ – коэффициент пропорциональности, называемый магнитной восприимчивостью вещества. Магнитные свойства вещества характеризуются также магнитной проницаемостью μ, показывающей, во сколько раз индукция магнитного поля в веществе (В) больше, чем в вакууме (В₀):

. (16.3)

Найдем связь между χ и μ.

В отсутствие магнетика магнитное поле создается только макротоками (токами проводимости); по определению (16.3) μ=1. Индукция магнитного поля в вакууме связана с напряженностью формулой:

. (16.4)

Напряженность магнитного поля – характеристика магнитного поля, описывающая только поле макротоков.

В магнетике, кроме поля макротоков, появляется еще индукция поля, созданного самим намагниченным веществом – микротоками (по Амперу, молекулярными токами) , пропорциональная вектору намагниченности:

. (16.5)

Полная индукция по принципу суперпозиции , а с учетом (16.2), (16.4) и (16.5):

. (16.6)

По определению (16.3) , то есть , и, сравнивая это выражение с (16.6), получим:

. (16.7)

В зависимости от знака и величины магнитной восприимчивости все вещества делятся на три группы:

1. Диамагнетиками являются вещества, которые намагничиваются во внешнем магнитном поле в направлении, противоположном направлению вектора магнитной индукции намагничивающего поля (J<0, χ<0, |χ|≈10^-6÷10^-8).

К диамагнетикам относятся вещества, магнитные моменты атомов, молекул или ионов которых в отсутствие внешнего магнитного поля равны нулю. Диамагнетиками являются инертные газы, молекулярные водород и азот, висмут, цинк, медь, золото,…

Диамагнетизм объясняется либо откликом на внешнее магнитное поле электронных оболочек атомов, либо откликом обобществлённых электронов проводимости (металлы). Эффект диамагнетизма есть не что иное, как электромагнитная индукция на уровне электронных (по Амперу, молекулярных) токов, присущих всем веществам.

2. Парамагнетики – вещества, у которых при отсутствии внешнего поля магнитные моменты атомов или молекул отличны от нуля: . Однако вследствие хаотической ориентации магнитных моментов атомов или молекул намагниченность отсутствует: . Во внешнем магнитном поле магнитные моменты вещества стремятся сориентироваться в направлении поля, в результате чего J>0 и χ>0 (χ≈10^-4÷10^-6). У парамагнетиков ориентация магнитных диполей происходит только за счёт внешнего поля на фоне теплового движения, и степень её обычно невелика.

Поскольку магнитная восприимчивость диа- и парамагнетиков очень мала, эти вещества относятся к слабомагнитным. Для них .

3. Ферромагнетики – твёрдые вещества, обладающие при не слишком высоких температурах самопроизвольной (спонтанной) намагниченностью, которая сильно изменяется под влиянием внешних воздействий – магнитного поля, деформации, изменения температуры.

Ферромагнетики, в отличие от слабомагнитных диа- и парамагнетиков, являются сильно магнитными средами: внутреннее магнитное поле в них может в сотни и тысячи раз превосходить внешнее поле. Такими свойствами обладают кристаллы переходных металлов (железо, кобальт, никель), некоторые редкоземельные элементы, ряд сплавов, а также некоторые металлические стёкла.

Ферромагнетики характеризуются следующими свойствами:

а) Если у пара- и диамагнетиков |μ–1|<<1, то у ферромагнетиков значение магнитной проницаемости достигает величин порядка μ≈10⁴ и более.

б) Если у диа- и парамагнетиков зависимость линейна и однозначна, то у ферромагнитных материалов она не только нелинейна, но зависит от предыстории образца. В частности, ферромагнетики могут существовать в виде постоянных магнитов.

в) В отличие от диа- и парамагнетизма, явление ферромагнетизма не может быть смоделировано в рамках классической физики; природа его – исключительно квантовая.

Ферромагнетизм обусловлен упорядоченной ориентацией спиновых магнитных моментов. Часть ферромагнетика, в которой все магнитные моменты при отсутствии внешнего поля устанавливаются в одном направлении, называется доменом (рис. 16.3,а). Домен обладает магнитным моментом . Размеры доменов составляют l=10^-8÷10^{-6 м. При отсутствии внешнего магнитного поля магнитный момент ферромагнетика вследствие хаотической ориентации намагниченности различных доменов.}

Между доменами А и В имеются переходные слои С (рис. 16.3, б) шириной l_перех.=10^-9…10^{-8 м. Внутри переходного слоя магнитные спиновые моменты ионов поворачиваются до тех пор, пока не примут нужного направления. Во внешнем магнитном поле переходные слои разрушаются. Магнитные моменты отдельных доменов поворачиваются в направлении магнитного поля (рис. 16.3, в).}

Зависимость намагниченности J магнетиков от напряженности Н внешнего магнитного поля изображена на рис. 16.4. Нелинейная область I отражает процесс ориентации доменов в ферромагнетиках в направлении внешнего поля при возрастании напряженности Н. В сильных полях (область II) наступает магнитное насыщение, и намагниченность практически не зависит от напряженности поля Н. Кривая зависимости намагниченности от напряженности магнитного поля носит название основной кривой намагничивания. Для пара- и диамагнетиков зависимость линейная.

Рис.16.4 Рис.16.5

Главная характеристика любого ферромагнетика – кривая гистерезиса, в котором проявляется зависимость намагниченности от предшествующего состояния. При циклических изменениях величины и направления напряженности внешнего поля Н эта зависимость характеризуется кривой, называемой петлей гистерезиса (рис. 16.5, кривые 1, 2, 3). Если ферромагнетик был первоначально размагничен (В=0, Н=0), то его намагничивание происходит по основной кривой намагничивания ОА. В точке А напряженность Н_Н и индукция В_Н соответствует состоянию магнитного насыщения. Размагничивание ферромагнетика происходит по кривой 1 (A-B_r-H_C-A¢). При Н=0 намагниченность ферромагнетика не исчезает: В= B_r.

Это состояние называется остаточным магнетизмом. Напряженность (–Н_С), при которой исчезает остаточная намагниченность (В=0, Н=–Н_С), принято называть коэрцитивной силой. Если при циклическом намагничивании H_max≥H_c, то мы получаем максимальную петлю гистерезиса 1. Кривые 2 и 3 – это частные циклы, когда H_max<H_c. Максимумы В и Н частных циклов лежат на основной кривой намагничивания ОА. Условно принято считать ферромагнетики магнитожесткими, если А/м. Если А/м, ферромагнетики считаются магнитомягкими. Магнитная проницаемость μ ферромагнетика зависит от напряженности магнитного поля Н (рис. 16.6). Магнитная проницаемость достигает максимума, когда напряженность Н внешнего поля становится равной напряженности Н_н, при которой домены максимально ориентируются по направлению поля (рис. 16.3, в) и при этом достигается магнитное насыщение образца. В табл. 16.1 приведены характеристики некоторых ферромагнетиков и ферритов.

Таблица 16.1

Вещество	mmax	Hс, А/м	Br, Тл
Железо техническое Супермаллой Сталь кобальтовая Феррит никель-цинковый	-	0.16	0.06 - 0.9 -

Нагревание ферромагнетика может привести к разрушению доменной структуры вследствие теплового движения атомов, тогда ферромагнетик теряет ферромагнитные свойства и превращается в парамагнетик. Температура, соответствующая такому переходу, называется точкой Кюри: Т_с.

Экспериментальная часть

Приборы и оборудование: звуковой генератор ГС-118 (PQ, рис.16.7 и 16.8), электронный осциллограф С1-150 (РО), модуль “явление гистерезиса” ФПЭ–07.