Приток к скважинам кольцевой батареи

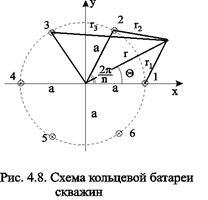
Пусть центры скважин располагаются в вершинах правильного n-угольника так, что скважины образуют кольцевую батарею радиуса а(рис. 4.8). Контур питания удалён от скважин на расстояние, значительно превышающее радиус батареи и тогда можно считать, что все скважины равноудалены от контура питания на расстояние r_к. Будем считать, что на контуре питания поддерживается постоянное значение потенциала j_к и на контуре скважин потенциал постоянен и равен j_с.В данной постановке, следовательно, надо решить задачу о плоском течении к nточечным стокам, размещённым равномерно на окружности радиуса а. Для получения формулы дебита скважин воспользуемся формулой 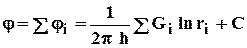(4.2) и получим:

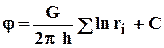, (4.20)

где G - массовый дебит любой скважины батареи, r_j- расстояния от некоторой точки пласта до всех nскважин; h - толщина пласта.

Граничные условия:

на контуре питания j=j_к=constпри r_j=r_к;

на контуре скважины j=j_с=constпри r₁=r_с;

r_j(j¹1)=2a sin[(n-1)p/n].

Используя данные граничные условия, преобразуем формулу (4.20)

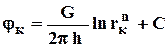, (4.21)

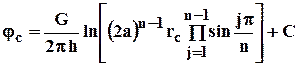. (4.22)

В последнем выражении

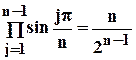. (4.23)

Тогда (4.22) перепишется в виде

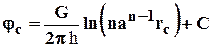(4.24)

И из (4.21), (4.24) получим выражение для определения дебита скважины

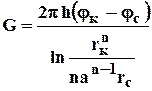(4.25)

Формула (4.25) справедлива при любом целом n. В частности, при n=1 имеем выражение типа формулы Дюпюи для определения дебита при плоскорадиальном потоке:

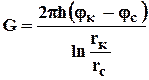. (4.26)

Формула (4.25) - приближенная. Её можно применять в случае, если размеры пласта во много раз больше площади внутри окружности батареи скважин, например, при водонапорном режиме, когда жидкость можно считать несжимаемой. Если же в пласте установился режим растворенного газа, то трудно ожидать, что площадь, занятая газированной жидкостью, простирается до границ пласта. Если расстояние до контура незначительно превышает радиус батареи, то, строго говоря, следует воспользоваться более точной формулой

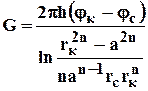(4.27)

Эта формула при n=1 переходит в формулу определения дебита эксцентрично заложенной одиночной скважины (а- эксцентриситет скважины). В большинстве практических случаев можно пользоваться формулой (4.25), т.к. уже при r_к=10а, дебиты подсчитанные по формулам (4.24) и (4.27), различаются не более чем на одну тысячную процента.

Определим дебит батареи, умножив формулу (4.25) на число скважин в батареи n

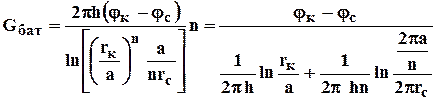. (4.28)

Рассмотрим поле течения в области действия круговой батареи, т.е. построим семейства линий тока и изобар. Уравнение изобар получаем из (4.3) 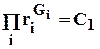путём представления радиусов r_j в полярной системе координат (рис.4.8).

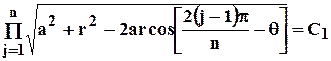. (4.29)

Данное уравнение позволяет построить поле изобар, а линии тока пересекают изобары под прямым углом.

Плоскость течения (рис. 4.9) кольцевой батареи с nравнодебитными скважинами, размещенными в вершинах правильного многоугольника, делится на nравных частей (секторов) прямыми линиями тока Н, сходящимися в центре батареи и делящими расстояние между двумя соседними скважинами пополам. Эти линии тока называются нейтральными. Другое семейство прямых линий тока Гпроходит через центры скважин и делит сектор, ограниченный двумя нейтральными линиями, пополам. Это - главные линии.

Семейство изобар подразделяется на два подсемейства, которые разграничиваются изобарой пересекающей себя в центре батареи столько раз, сколько скважин составляет данную батарею. Первое подсемейство изобар определяет приток к отдельным скважинам и представляет собой замкнутые, каплеобразные кривые, описанные вокруг каждой скважины. Второе семейство - определяет приток к батареи в целом и представляет собой замкнутые кривые, описанные вокруг батареи.

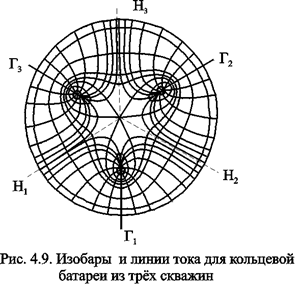
Скорость фильтрации по главным линиям максимальна, а по нейтральным линиям - минимальна. В центре кольцевой батареи скорость фильтрации равна нулю, т.е. частица жидкости, находящаяся в точке, в которой изобара пересекает сама себя, неподвижна. Такие точки фильтрационного поля называются точками равновесия и при разработке в окрестностях таких точек образуются “застойные области”. В условиях водонапорного режима в этих областях могут возникать “целики нефти”. Зная положения точек равновесия в пласте, можно находить рациональные приёмы для своевременной ликвидации целиков нефти. Одним из таких приёмов является изменение режима работы скважин, заставляющее нефть целика прийти в движение в нужном направлении.

Для кольцевой батареи, на основе анализа формул (4.25)-(4.28), можно сделать ряд оценок эффекта взаимодействия:

* дебит изменяется непропорционально числу скважин и радиусу батареи (расстоянию между скважинами);

* с увеличением числа скважин дебит каждой скважины уменьшается при постоянном забойном давлении, т.е. растет эффект взаимодействия;

* взаимодействие скважин может практически не проявляться только при очень больших расстояниях между скважинами (в случае несжимаемой жидкости, строго говоря, влияние скважин распространяется на весь пласт);

* с увеличением числа скважин темп роста суммарного дебита батареи замедляется (рис. 4.1), а именно, сверх определённого предела увеличение числа скважин оказывается неэффективным в виду прекращения прироста дебита.