Замечание о переменной интегрирования в неопределённом и определённом интеграле

Тема. Определённый интеграл.

Занятие 9.

Рассмотрим математический символ

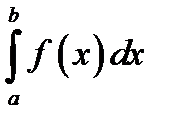, (9.1)

называемый определённым интегралом. Определённый интеграл зависит от чисел 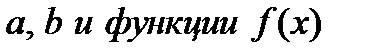,заданной на отрезке 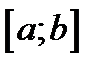, и обозначает некое число.

Сравним два символа: 1) 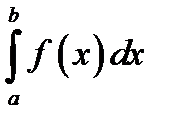и 2)

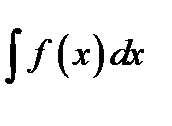
Первый задаёт число, а второй функцию.

Определение определённого интеграла.

Определение 9.1.

1 шаг. Разобьём отрезок 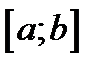наугад точками 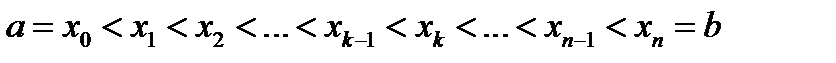на 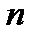малых ячеек 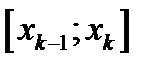. Будем обозначать длину каждой ячейки 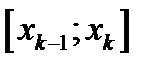так: 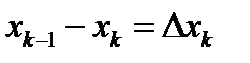Длину наибольшей ячейки обозначим через , .

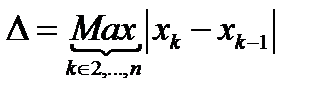2 шаг. На каждой из ячеек 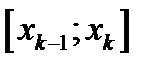наугад выберем точку 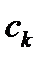, и вычисляем значение функции в выбранной точке 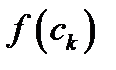. Составляем произведение .

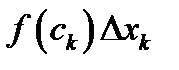3 шаг. Составляем сумму из всех этих произведений 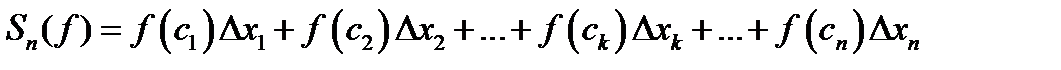(9.2)

Эта сумма называется интегральной суммой. Интегральная сумма зависит: 1) от разбиения на ячейки и 2) выбора точек 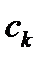в каждой ячейке.

Чтобы получить значение (число) дающее определенный интеграл нужно в интегральной сумме перейти к пределу при .

4 шаг. Если существует предельное значение интегральной суммы , то это предельное значение называется определённым интегралом

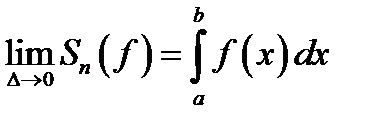(9.3)

Замечание. Предельное значение не должно зависеть

1) От способа разбиения отрезка 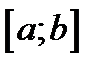на ячейки,

2) и от выбора точек .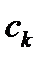

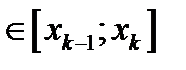Функция , у которой существует предельное значение интегральной суммы (9.3) называется

функцией интегрируемой на отрезке .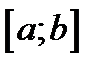

Теорема 9.1. Если функция непрерывна на отрезке 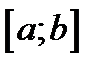, то определённый интеграл от неё существует.

Теорема 9.2. Если функция на отрезке 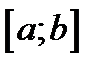имеет конечное число разрывов скачков, то определённый интеграл от неё существует.

Замечание. Четырёхшаговый алгоритм из определения 9.1, который определяет определённый интеграл не годится для его точного вычисления из-за четвёртого шага. Но если известна первообразная функция , то определённый интеграл легко вычисляется.

Основная теорема математического анализа.

Теорема Ньютона –Лейбница.

Теорема 9.2. Пусть на отрезке 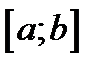задана непрерывнаяфункция 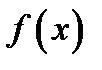. И пусть 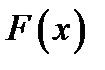любая из первообразных от функции 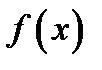. Тогда справедлива знаменитая формула Ньютона – Лейбница

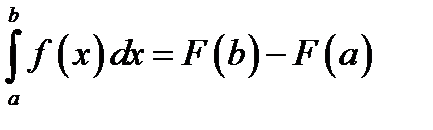(9.4)

Доказательство. Разобьём отрезок 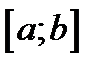точками 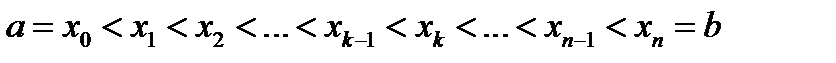на 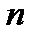малых ячеек 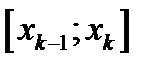и рассмотрим интегральную сумму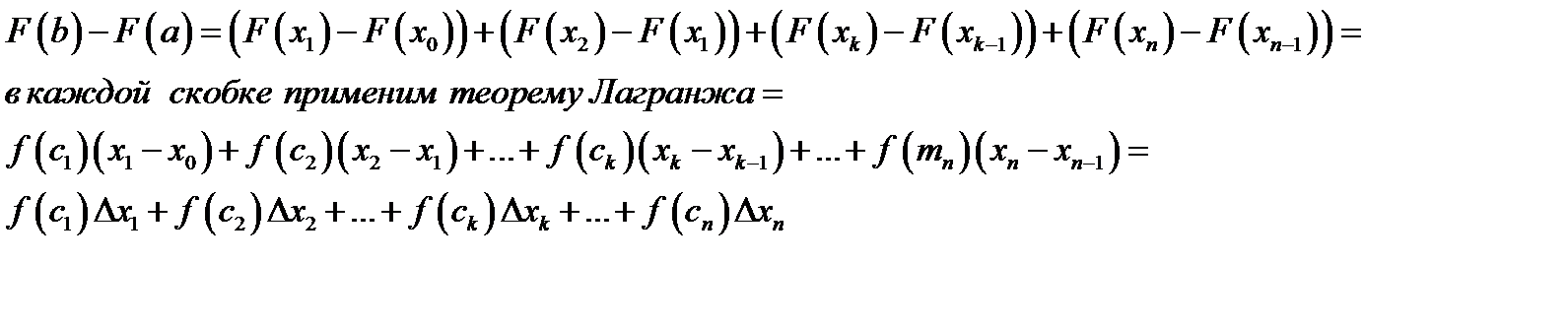

поскольку интегральная сумма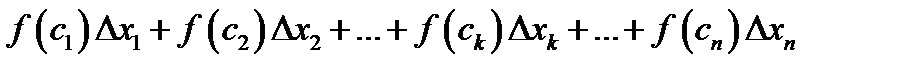

при любом делении на ячейки есть постоянное число 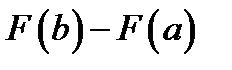, то и предельное значение суммы при 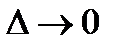не изменится. По условию функция 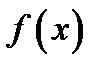непрерывна и поэтому по теореме 9.1 предел рассмотренной интегральной суммы и есть определенный интеграл

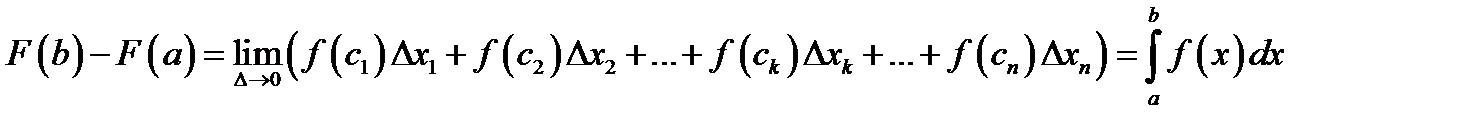(9.5)

Теорема доказана.

Замечание. Формулу Ньютона-Лейбница кратко записывают так

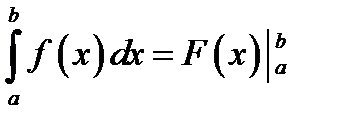
Замечание о переменной интегрирования в неопределённом и определённом интеграле.

Переменная 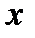, стоящая под знаком интеграла в определённом и неопределённом интегралах: 1) 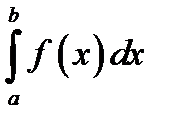и 2) 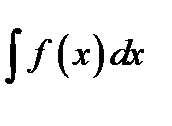называется одинаково- переменная интегрирования.

Однако в определённом интеграле результат интегрирования не зависит от того какой буквой

обозначена переменная: .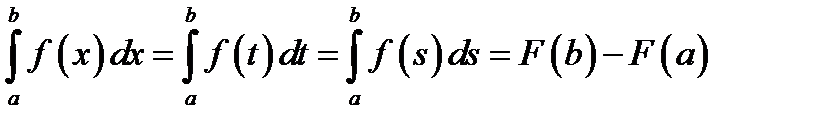

В неопределённом интеграле результат интегрирования зависит от того какой буквой обозначена переменная: 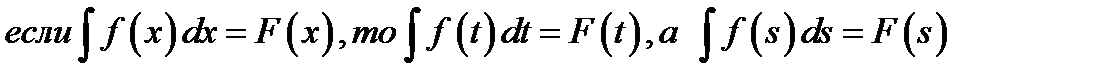. То есть в результате неопределённого интегрирования получаются функции разных аргументов.

Пусть функция 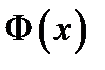есть первообразная от функции 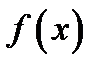. Это значит, что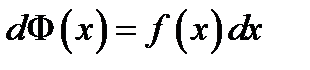

Рассмотрим функцию

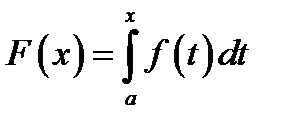(9.6)

Дифференциал этой функции

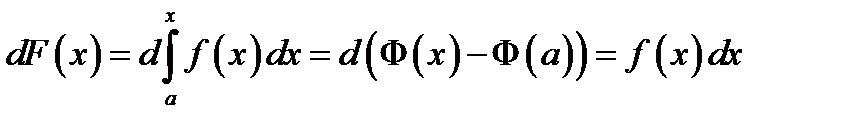
Следовательно, функция 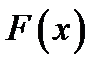= 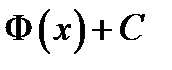является первообразной