Процесс заряда конденсатора

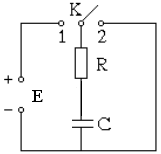Соединим последовательно незаряженный конденсатор С, резистор R и источник ЭДС Е с пренебрежимо малым внутренним сопротивлением (рис.1). Ключ К находится в положение 1. При этом конденсатор начинает заряжаться через сопротивление R.

Рис. 1.

Согласно второму правилу Кирхгофа для этой цепи можно записать:

Е = UС + UR

(1)

Из определения емкости конденсатора

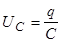(2)

По закону Ома

UR = IR

(3)

Подставляя (2) и (3) в (1), получаем:

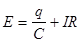(4)

Продифференцируем это выражение по времени:

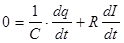(5)

Учитывая, что, по определению, сила тока I есть отношение dq к dt и разделяя переменные, получаем дифференциальное уравнение

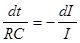(6)

Его решением будет выражение:

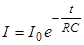(7)

где I₀ – постоянная, определяемая из начальных условий: в начальный момент (t = 0) U_C = 0, поэтому, из (1):

E = I0 R и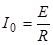

(8)

Найдем вид зависимости U_C от времени. Из (1):

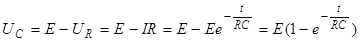(9)

Итак, ток в процессе заряда конденсатора экспоненциально уменьшается, а напряжение на конденсаторе экспоненциально возрастает.