Алгоритм построения фундаментальной системы циклов

1. Построить любое остовное дерево 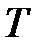исходного графа .

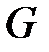2. Добавить к 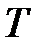некоторое ребро 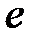, которое является ребром графа, но не принадлежит остову.

3. После такого добавления образуется цикл .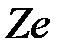

4. Все циклы 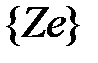(соответствующие всем ребрам, взятым не из остова) образуют фундаментальную систему циклов.

55. Задача комівояжера. Приклади практичних задач, що зводяться до задачі комівояжера.

Задача коммивояжера(Traveling salesman problem)

Коммивояжер должен посетить каждый из n городов по одному разу, выехав из некоторого из этих городов и вернувшись в него же. Требуется найти кратчайший маршрут, зная расстояния между каждой парой городов. Математическая постановка этой задачи состоит в следующем: в полном взвешенном графе требуется найти гамильтонов цикл (или цепь) наименьшего веса (длины).

Данная задача является NP-полной; для ее решения не существует эффективного алгоритма. Важность этой задачи связана с тем, что к ней сводятся многие другие задачи; в связи с чем она играет роль эталонной задачи.

56. Дерева. Визначення дерева, властивості дерев, ліс.

Связный граф, не содержащий циклов, называется деревом.

Несвязный граф, не содержащий циклов, называется лесом.

Свойтва дсеревьев

Теорема 21.1. Всякое дерево содержит 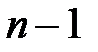ребер, где 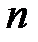– число вершин.

Теорема 21.2. Всякий лес содержит 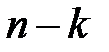ребер, где 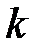– число компонент связности.

Теорема 21.3. Любые две вершины дерева соединены точно одной простой цепью.

Теорема 21.4. Если в дереве любые две вершины соединить ребром, то в графе появится один цикл.

57. Перелічення графів і дерев. Остови графа.

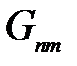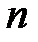Количество (неориентированных) помеченных графов (простых с вершинами и 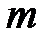ребрами) равно числу сочетаний из множества различных неориентированных пар вершин 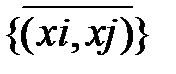по числу ребер .

,

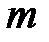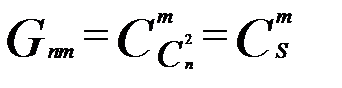Суммируя числа 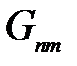по всем возможным количествам ребер 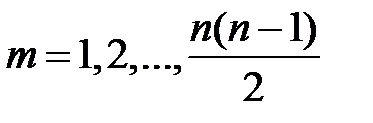от случая безреберного графа до случая полного графа с вершинами, получаем число всех помеченных графов с 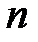вершинами:

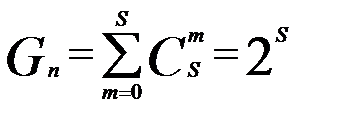
Формула А. Кэли. Число 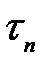помеченных деревьев с 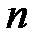вершинами равно 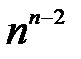, т.е. .

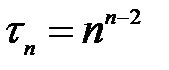Остовом называется связный частичный граф данного связного графа 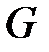, содержащий все вершины графа 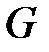, но не содержащий циклов.

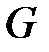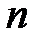Теорема Кирхгофа. Число остовных деревьев в простом связном графе с вершинами равно алгебраическому дополнению любого элемента матрицы Кирхгофа .

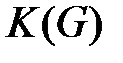58. Орієнтовані і бінарні дерева. Правила обходу бінарних дерев. Еквівалентні бінарні дерева.

Ориентированное дерево (корневое ориентированное дерево) (рис. 21.12) – это ориентированный граф без циклов со свойствами:

1. Существует в точности одна вершина 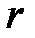, называемая корнем, в которую не заходит ни одна дуга.
2. В каждую вершину, кроме корня, заходит в точности одна дуга.
3. Существует путь из корня в любую другую вершину.

Бинарное (двоичное) дерево 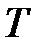– это упорядоченное дерево, из каждой вершины которого может исходить не более двух дуг. Ориентированное дерево называют бинарным, если полустепень исхода любой его вершины не больше 2.

Над бинарным деревом есть операция – его прохождение, т.е. нужно обойти все дерево, отметив каждый узел один раз.

Существует 3 способа обхода бинарного дерева:

1. В прямом порядке.

2. В симметричном порядке.

3. В обратном порядке.

В прямом порядке (обход в прямом порядке, прямой обход, упорядоченный обход, обход сверху, обход в ширину, preorder):

1. Попасть в корень.

2. Пройти в прямом порядке левое поддерево.

3. Пройти в прямом порядке правое поддерево.

В симметричном порядке (обход симметричным способом, симметричный обход, inorder):

1. Пройти в симметричном порядке левое поддерево.

2. Попасть в корень.

3. Пройти в симметричном порядке правое поддерево.

В обратном порядке (обход в обратном порядке, обход в глубину, обратный обход, обход снизу, postorder):

1. Пройти в обратном порядке левое поддерево.

2. Пройти в обратном порядке правое поддерево.

3. Попасть в корень.

59. Розфарбування графів. Фарбування вершин та ребер. Хроматичне число, теорема про біхроматичний граф. Хроматичний клас. Теорема Брукса.

Раскраской вершин графа называется назначение цветов его вершинам. Обычно цвета – это числа 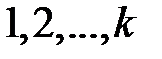. Раскраска называется правильной, если каждый цветной класс является независимым множеством. Иначе говоря, в правильной раскраске любые две смежные вершины должны иметь разные цвета. Задача о раскраске состоит в нахождении правильной раскраски данного графа в наименьшее число цветов. Это число называется хроматическим числом графа и обозначается .

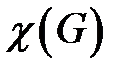Наименьшее число цветов для правильной раскраски называется хроматическим классом 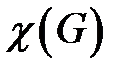графа или индексом.

Если граф имеет хроматическое число 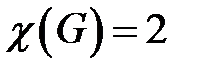, то его называют бихроматическим графом. Любое раскрашивание 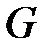2 красками разбивает вершины на 2 множества 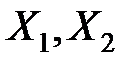, посередине каждого множества вершины попарно несмежные (или независимы).

Теорема (Брукса). Пусть 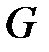– простой связный граф, не являющийся полным; если наибольшая из степеней его вершин равна 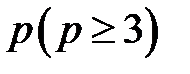, то он 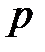-раскрашиваем.

Теорема Кенига.Граф 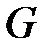называется бихроматическим тогда и только тогда, когда все его циклы имеют четную длину.

60. Гіпотеза чотирьох фарб. Теорема про п'ять фарб. Прикладні задачі, що зв’язані з розфарбуванням графів

Гипотеза четырех красок для карт: всякая карта 4-раскрашиваема.(удалось обосновать с использованием ЭВМ).

Хівуд(1890р) – проблема 4 фарб, довів що достатньо 5.

Задачи: Определение раскрашиваемости карт/графов(k-раскрашиваемый).

61. Двудольні та k-дольні графи.

Неориентированный граф 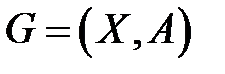называют двудольным, если множество его вершин 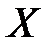может быть разбито на такие два подмножества 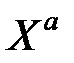и 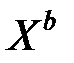, что каждое ребро имеет один конец в 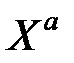, а другой в .

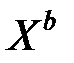Ориентированный граф 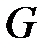называется двудольным, если его неориентированный двойник – двудольный граф.

Теорема о двудольности.Граф 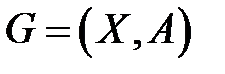является двудольным тогда и только тогда, когда он не содержит циклов нечетной длины.

62. Найкоротші відстані та шляхи у мережах. Алгоритм визначення відстані між вершинами на графі з одиничними довжинами ребер. Алгоритм Дейкстри (Форда) визначення відстані між вершинами на графі з довільними довжинами ребер.

Маршрут, циклический маршрут, цепь, путь(ориентированная цепь).

Алгоритм Дейкстры решает задачу о кратчайших путях из одной вершины для взвешенного ориентированного графа.

Каждой вершине из 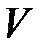сопоставим метку — минимальное известное расстояние от этой вершины до . Алгоритм работает пошагово — на каждом шаге он «посещает» одну вершину и пытается уменьшать метки. Работа алгоритма завершается, когда все вершины посещены.

63. Алгоритми Флойда і Данцига пошуку найкоротших шляхів між всіма парами вершин графа.

Алгоритм Флойда

Формулировка задачи. Дан непустой взвешенный граф с произвольными весами ребер. Требуется найти кратчайшие длины путей между всеми парами вершин графа, если в графе нет циклов отрицательной длины или обнаружить наличие таких циклов.

Алгоритм

Инициализация структур данных.

Строится матрица 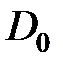размерности 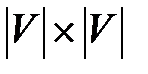, элементы которой определяются по правилу: ;

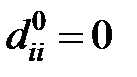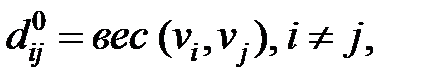если в графе существует ребро (дуга) ;

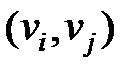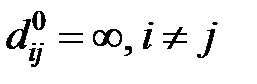, если нет ребра (дуги) .

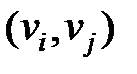Основная часть алгоритма:

Выполнять цикл, завершение которого наступает по выполнению одного из двух условий: либо количество шагов цикла равно 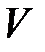, либо был обнаружен цикл отрицательной длины. Шаги цикла нумеруются с нуля. Шаг цикла будем обозначать переменной .

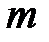Строится матрица с индексом равным номеру шага, обозначим его через 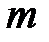, в которой элементы определяются через элементы матрицы предыдущего шага по следующим формулам:

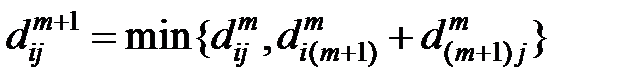, где . (*)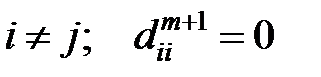

Если 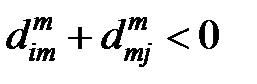для какого-то 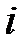, то в графе существует цикл (контур) отрицательной длины, проходящий через вершину .

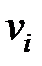По завершению работы данного алгоритма, элементы матрицы равны длинам кратчайших путей между соответствующими вершинами.

Поиск путей

Если требует найти сами пути, то перед началом работы алгоритма построим матрицу P с начальными значениями элементов 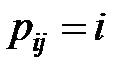. Каждый раз, когда на шаге (1) значение 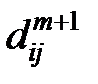будет уменьшаться в соответствии с (*) (т.е. когда 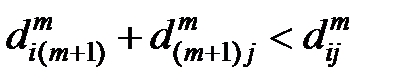), выполним присваивание 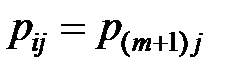. В конце работы алгоритма матрица P будет определять кратчайшие пути между всеми парами вершин: значение p_ij будет равно номеру предпоследней вершины в пути между 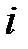и (либо 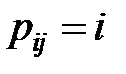, если путь не существует).

Примечаниe: если граф - неориентированный, то все матрицы 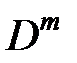являются симметричными, поэтому достаточно вычислять элементы, находящиеся только выше (либо только ниже) главной диагонали.

Алгоритм Данцига

Перенумеровать вершины графа, определить матрицу 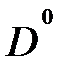размером 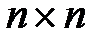где 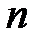число вершин графа. Каждый элемент этой матрицы есть длина кратчайшей дуги от одной вершины до другой.

Для каждого m принимающего значения 1,2,3…N определить матрицу 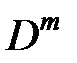по формулам (2) – для строки 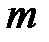, (3) – для столбца 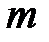, (1) – для всех остальных элементов, кроме диагонального .

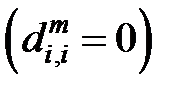64. Течії у мережах. Задача про максимальну течію у мережі. Розріз мережі. Теорема про максимальну течію і мінімальний розріз. Алгоритм Форда-Фалкерсона.

Транспортной сетью называется пара 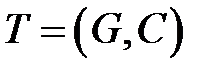, где 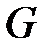– взвешенный орграф, удовлетворяющий следующим условиям:

а) нет петель;

б) существует только одна вершина, не имеющая ни одного прообраза – это исток;

в) существует только одна вершина, не имеющая ни одного образа – это сток;

Потоком в транспортной сети 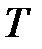называется неотрицательная вещественная функция, определенная на множестве дуг, удовлетворяющая условиям:

– ограниченности: поток по любой дуге сети не превосходит пропускной способности этой дуги;

– сохранения: суммарный поток, заходящий в любую вершину сети (кроме истока и стока) равен суммарному потоку, выходящему из этой вершины.

Величиной потока называется сумма значений этой функции по всем выходным дугам сети (выходные дуги сети – это дуги, инцидентные стоку) .Понятия потока и величины потока в сети часто путают, однако между ними существует различие: поток – это функция, а величина потока – число.

Разрезом сети называется множество, которому принадлежит исток, и не принадлежит сток. Т.е. разрез – это минимальное (в смысле отношения включения) множество дуг, удаление которых “разрывает” все пути, соединяющие исток и сток.

В любой транспортной сети величина любого максимального потока равна пропускной способности любого минимального разреза.

65. Елементи теорії формальних граматик. Задачі формалізації мов та перекладу. Задання мов за допомогою граматик. Типи граматик.

Задача формализации языка и перевода заключается в переводе с алгоритмического языка на машинный с одновременной оптимизацией программы, определение корректности записи, которая переводится.Формальный алфавит– это множество символов. Обозначается большой латинской буквой, символ – маленькой с индексом или без. Строка – это конечная последовательность букв алфавита, это элемент декартова произведения. Язык – это множество строк конечной длинны в заданном конечном алфавите. Грамматика – это система, которая позволяет описать язык. Грамматика, которая распознает – это грамматика, которая может определить является ли данная строка правильной, или нет. Грамматика, которая порождает – может построить правильную строку.

Типы грамматик:

- Общего вида,

- Контекстно-зависимая

- Контекстно-свободная

- Праволинейная

66. Елементи теорії скінчених автоматів. Загальна характеристика автоматів. Розпізнавачі.

Автомат – это схематизированный алгоритм. Состоит из входной ленты (последовательность клеток, в которых хранятся символы алфавита), управляющего устройства (читает содержание клеток) и рабочей памяти (структура, в которой хранятся данные, которые используются при работе).

Распознаватели –это автоматы, которые используются для распознавания языка.

67. Скінченні автомати. Способи задання автоматів. Автомати Мили і Мура. Автомати з магазинною пам’яттю. Машина Тьюринга.

Конечный автомат – это автомат, который состоит из входной ленты и управляющего устройства с конечной памятью. Число его состояний – конечно, а входная головка – односторонняя, смещается только вправо.

Конечный автомат можно задать с помощью:

- таблицы (для каждого состояния и входного символа указывается следующее состояние и выходной символ)

- диаграммы состояний (ориентированный граф) (вершины – состояний, дуги – переход из одного состояния в другой)

Автомат Мили – это конечный автомат, у которого входная информация поставлена в соответствие с переходами.

Автомат Мура – это конечный автомат, у которого выходная информация поставлена в соответствие с состоянием.

Автомат с магазинной памятью – это конечный автомат, который имеет прибор памяти – стек.

Машина Тьюринга – это самый мощный автомат, содержит все элементы конечного автомата, кроме того ее лента имеет бесконечный размер, головка, которая считывает также и печатает, может перемещаться во всех направлениях.