Заряд конденсатора

Переведем ключ К на схеме (рис. 1) из положения 2 в положение 1. В результате начнется заряд конденсатора от батареи, имеющей ЭДС e, через сопротивление R.

Уравнения, описывающие заряд конденсатора, аналогичны выражениям (1)

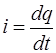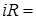, e–U, q=CU. (7)

Предполагаем, что внутреннее сопротивление источника тока пренебрежимо мало по сравнению с величиной R. Теперь ток в цепи считается положительным, когда он течет в направлении положительно заряженной обкладки конденсатора. Исключая в уравнениях (7) силу тока i и напряжение на конденсаторе U, получим уравнение:

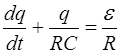. (8)

Запишем уравнение (8) в следующем виде:

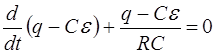. (9)

Решая это уравнение, получим

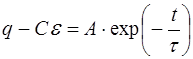. (10)

Коэффициент А най-дем из начальных условий, а именно, q=0 при t=0 :

A=–Ce.

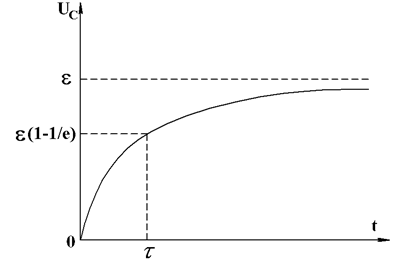
Рис. 3

В результате получаем зависимость q(t):

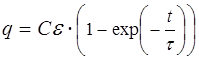. (11)

Поделив обе части уравнения (11) на С, получим зависимость напряжения на конденсаторе U от времени

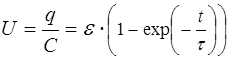. (12)

Зависимость U(t) показана на рис. 3. Подставив в (12) значение напряжения, равного 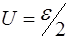, получим

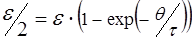, (13)

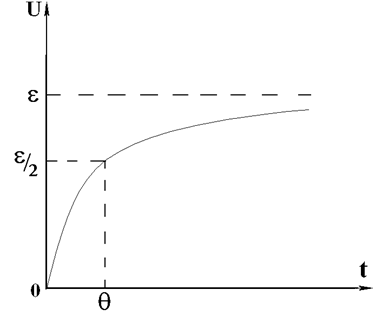где q – время, за которое напряжение на конденсаторе вырастает до половины своего максимального значения ( рис. 4). Отсюда время

q=t×ln2»0,7t.

Следовательно, дли-тельность заряда до по-ловины максимального значения напряжения на конденсаторе будет та-кой же, как и при разряде конденсатора (см. (6)).

Рис. 4