Определение несоответствия периодов кристаллических решеток подложки и пленки в эпитаксиальных структурах. Определение состава пленок из рентгенодифракционных данных

Методические указания по выполнению лабораторной работы по курсу

«Методы исследования и моделирования нанообъектов, приборов и нанотехнологических процессов»

Калуга , 2015 г.

УДК 621

Методические указания издаются в соответствии с учебным планом направления подготовки 28.04.02Наноинженерия.

Методические указания рассмотрены и одобрены:

кафедрой «Материаловедение »(ЭИУ4-КФ)

протокол № 1 от « 30 » августа 2015 г.

Зав. кафедрой ЭИУ4-КФ_______________ д.т.н., профессор Косушкин В.Г.

Авторы: __________ доцент кафедры ЭИУ4-КФ, к.ф.-м.н. Прохоров И.А.

Аннотация

В методических указаниях приведены: цель выполнения лабораторной работы по дисциплине «Методы исследования и моделирования нанообъектов, приборов и нанотехнологических процессов», исходные данные, порядок выполнения и содержание, требования к оформлению, список рекомендуемой литературы.

* Калужский филиал МГТУ им.Н.Э.Баумана 2015 г.

* Прохоров И.А.

Цель работы: изучить теоретические основы определения несоответствия периодов кристаллических решеток подложки и пленки из дифракционных данных, полученных с использованием двух геометрий дифракции, и их использование для определения состава пленок.

Задача работы: определить несоответствие периодов кристаллических решеток подложки и пленки и состава пленок из рентгенодифракционных данных.

Образец ТШ-3.

CVD ¹³C/ HPHT Ib, толщина пленки ~ 2 мкм.

Ориентация подложки (001), максимальная разориентация составляет ~ 2°.

Рис. 1. Фотография образца ТШ-3 со стороны пленки. Ориентация (001), боковые стороны соответствуют направлениям типа <110> (в отличие от образца E6, где было <001>). Темное пятно – метка со стороны подложки. Белым квадратом отмечена область размером ~ 1 × 1 мм², в которой проводились дифрактометрические измерения (остальная часть кристалла была закрыта свинцовой фольгой).

Исследования проведены на двухкристальном рентгеновском дифрактометре в CuK_a1 излучении с использованием германиевого монохроматора: отражение 511, угол Брэгга q ~ 45,07°, фактор асимметрии отражения b ~ 0,01 (расходимость пучка после монохроматора составляет ~ 0,5"). При использовании асимметричного отражения 113 от алмазного образца (угол Брэгга q ~ 45,75°, угол выхода отражающей плоскости к поверхности образца j = 25,24°) это обеспечило, практически бездисперсионную схему дифракции. Полуширина кривой качания асимметричного отражения 113 для подложек из алмаза типа Ib составила 4,9" (оценка для симметричного отражения дает величину w_s = w·√b ~ 3", где b = sin(q – j) / sin(q + j) – фактор асимметрии отражения от образца), пиковый коэффициент отражения R ~ 0,73.

Кривые качания, полученные в отражении 113 (выход отражающих плоскостей к поверхности пленки составляет φ = 25.24°) в топографическом режиме (с полным омыванием образца пучком) уширены и содержат два доминирующих пика, сформированных отражениями от подложки и пленки. Кроме того, выявляются дополнительные пики, связанные, по-видимому, с отражением от различных слегка разориентированных секторов роста.

Ограничение области отражение на образце (белый квадрат на Рис. 1) позволило значительно улучшить параметры кривых качания. Для ω_A геометрии дифракции (Рис. 2 а) полуширины кривых качания для подложки и пленки составили Dω^S_A1/2~2.9" и Dω^L_B1/2~4.0", соответственно (Рис. 3. а). Для ω_B геометрии (Рис. 2 б) полуширины кривых качания для подложки и пленки составили Dω^S_A1/2~5.3" и Dω^L_B1/2~10.6", соответственно (Рис. 3. б). Отражение от пленки расположено со стороны бóльших углов (что соответствует меньшим значениям межплоскостного расстояния) и характеризуется бóльшим значением полуширины кривой качания.

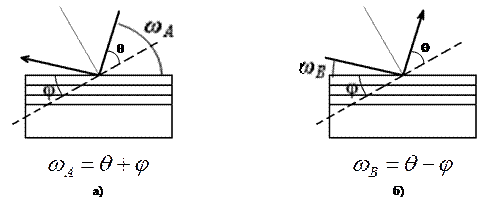Рис. 2. Геометрии дифракции, используемые для определения несоответствия периодов кристаллических решеток подложки и пленки.

а) - ω_A геометрия дифракции с углом падения излучения на образец ω_A=q + φ;

б) - ω_B геометрия с углом падения излучения на образец ω_B = θ – φ,

где θ- угол Брэгга, φ- угол выхода отражающих плоскостей к поверхности образца.

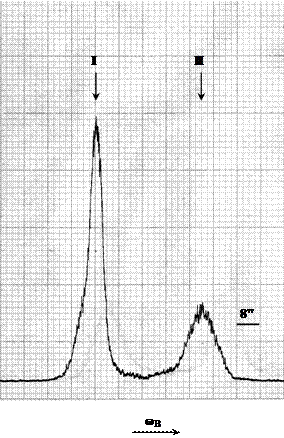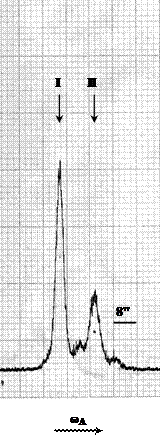
Рис. 3. Кривые качания, полученные в двух геометриях дифракции от области образца, отмеченной белым квадратом на Рис. 1. CuK_a1 излучение, отражение 113, выход отражающих плоскостей к поверхности пленки составляет φ = 25.24°. I– пик отражения от подложки, II – пик отражения от пленки. Угловые расстояния между пиками отражений от подложки и пленки составляют Dω_A = 12.3" и Dω_B = 38.4". Искажение формы кривых качания и появление дополнительных пиков обусловлено, по-видимому, неоднородностью подложки.

Угловые расстояния между пиками отражения от подложки и пленки, полученными в двух геометриях дифракции, составляют Dω_A = 12.3" и Dω_B = 38.4". Известно [1], что полусумма этих расстояний дает изменение брэгговского угла Dθ = (Dω_A + Dω_B)/2 = 25.4", а полуразность равна взаимной разориентации отражающих плоскостей Dφ = (Dω_A – Dω_B)/2= 13.1".

Используя известные соотношения (Ур. 1 и Ур. 2 [1]), где (Dd/d)_^ - изменение межплоскостных расстояний перпендикулярно поверхности пленки:

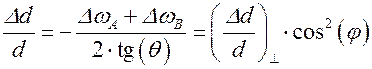1)

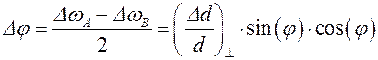2)

находим для относительного изменения межплоскостного расстояния (113) (Dd/d)₁₁₃ ~ 1.19·10^–4. Из уравнения 1 находим, что (Dd/d)_^ ~ 1.45·10^–4. Изменение релаксированного (в свободном, недеформированном состоянии) периода решетки равно (Dа/а)_relax = g· (Dd/d)_^, где g·– корректировочный фактор. Для ориентации подложки (001) g₀₀₁ = С₁₁/(С₁₁+ 2С₁₂), где С₁₁ и С₁₂ упругие постоянные. Для алмаза g₀₀₁ = 0.81.

Таким образом, изменение периода кристаллической решетки алмаза при полном изотопическом замещении составило по результатам проведенных измерений (Dа/а)_relax ~1.2 ·10^–4.

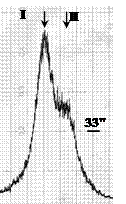
Использование симметричного отражения 004 позволяют непосредственно из одного измерения определить (Dd/d)_^. Однако, из-за дисперсионного уширения кривых качания (угол Брэгга для отражения 004 составляет θ ~ 59.75°, что значительно отличается от брэгговского угла отражения от монохроматора, q ~ 45,07°) пики отражения от подложки и пленки разделяются хуже, чем в отражении 113 (Рис. 4).

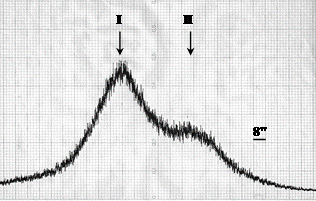Рис. 4. Кривые качания от области образца, отмеченной белым квадратом на Рис. 1., полученные в отражении 004 при различных скоростях вращения образца. I– пик отражения от подложки, II – пик отражения от пленки. Угловое расстояние между пиками составляет Dθ ~ 50".

Для относительного изменения межплоскостных расстояний перпендикулярно поверхности пленки получаем (Dd/d)_^= – ctg θ·Dθ ~ 1.4·10^–4. Изменение релаксированного периода решетки равно (Dа/а)_relax = g· (Dd/d)_^ ~ 1.14·10^–4, что, практически, совпадает с результатами, полученными с использованием асимметричного отражения 113. Учет незначительного изменения упругих постоянных для алмаза ¹³С, практически, не влияет на результаты расчета.

Таким образом, результаты измерений с использованием симметричного и асимметричного отражений дают примерно одинаковое значение для величины несоответствия в периодах кристаллических решеток Ib подложки и ¹³С CVD пленки (Dа/а)_relax ~ (1.1¸1.2)·10^–4.

[1] W.J. Bartels, W. Nijman. J. Cryst. Growth, 44(1978) 518-525.

ПРИЛОЖЕНИЕ