Смешанные стратегии. Решение игр в смешанных стратегиях.

Если 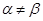, то можно улучшить нашу нижнюю границу путём смешивания чистых стратегий, т. е. изменением стратегии от одной к другой от одного этапа игры к другому. Для каждой конкретной игры можно установить: 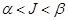. Здесь 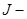цена игры; 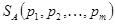, вероятность приме­нения стратегии 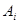; 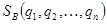, 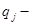вероятность применения стратегии .

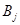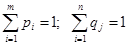– свойство полноты.

С применением смешанных стратегий всегда можно найти решение, обладающее устойчивостью. Решением игры называется пара оптимальных смешанных стратегий 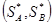обладающих следующим свойством: если один из игроков придерживается своей оптимальной смешанной стратегии, то другому не может быть выгодно отступать от своей. Выигрыш соответствующего оптимального решения называется ценой игры.

Основная теорема теории игр.

Каждая конечная игра имеет по крайней мере одно решение, возможно в области смешанных стратегий. Цена игры заключена в пределах 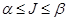. Введём понятие активной стратегии – стратегии, которая входит в решение с вероятностью большей нуля.

Теорема об активных стратегиях: если один из игроков придерживается своей оптимальной смешанной стратегии, то выигрыш остается неизменным и равен цене игры 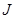независимо от того, что делает другой игрок, если только тот не выходит за пределы своих активных стратегий.

Доказательство: пусть получена оптимальная стратегия 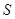игрока :

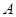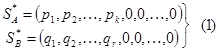
Применение решения (1) дает выигрыш 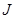. Пусть 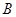пользуется чистыми стратегиями, в результате получим выигрыш .

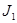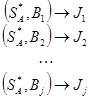
По определению решения игры следует, что отклонение от своей стратегии невыгодно для игрока: 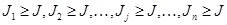. Посмотрим, может ли быть 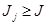, т. е. существует ли такое 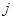. Выразим цены игры, полученные при применении смешанной стратегии как величину математического ожидания: 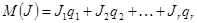. . 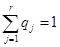Получается, что чистая цена игры – это математическое ожидание, если какая-то случайная величина 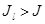, а все остальные равны 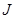, то среднее значение должно быть больше 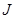, а не равно ему, так как ни одна случайная величина не может быть больше МО.

Упрощение игр.

Если 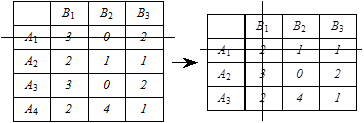в игре построена платёжная матрица, то игру возможно упростить, т. е. заранее отбросить такие стратегии игроков, которые не могут быть выгодными ни при каких обстоятельствах. Итак вычёркиваем заведомо невыгодные и дублирующие стратегии: дублирующая стратегия – это строка 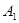. Стратегия 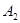заведомо невыгодна, а при просмотре столбцов – невыгодны большие векторы, поэтому 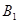так же вычёркиваем.

Таким образом, если записана платёжная матрица, нужно её упростить, вычислить 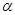и , и 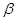если они не равны друг другу, принимаются за решение смешанной стратегии.

Решение игр .

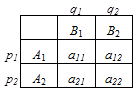Если в такой игре нет седловой точки, то все стратегии являются активными. Если же седловая точка есть, то игра может быть решена путём отбрасывания заведомо невыгодных решений. Все стратегии активные, значит можно применить теорему об активных стратегиях:

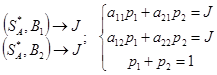
Решая эту систему получим:

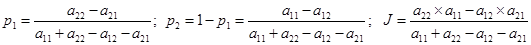
Для игрока :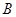

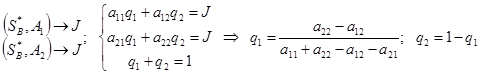
Пример: игра в «прятки»: