Приборы и принадлежности Математический маятник, секундомер

Теория работы и описание приборов

Ускорение свободного падения g измеряется различными методами. В данной работе g определяется при помощи математического маятника. Математическим маятником называется материальная точка весом 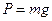, подвешенная на гибкой, невесомой и нерастяжимой нити (рис. 1).

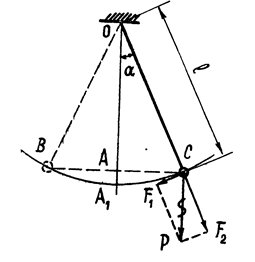
Рис. 10

В данном случае материальной точкой можно считать физическое тело с массой m, если его размерами можно пренебречь по сравнению с длиной подвеса. В вертикальном положении сила тяжести материальной точки

P полностью уравновешивается натяжением нити, и маятник остается в положении равновесия.

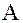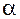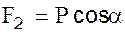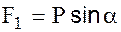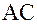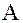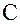Если маятник отклонить от положения равновесия на некоторый угол , то составляющая силы тяжести, направленная вдоль нити, т.е. сила , уравновесится натяжением нити; другая же составляющая, т.е. сила , перпендикулярная к нити, будет стремиться вернуть маятник в положение равновесия. Расстояние , на которое маятник отклонится от положения равновесия, называется смещением. Если смещение от к считать положительным, а от 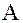к 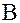– отрицательным, то сила 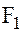всегда будет направлена обратно смещению, и при малых углах (5° – 6°) пропорциональна смещению .

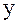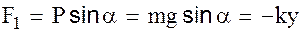(1)

Согласно определению гармонического колебания, возвращающая сила прямо пропорциональна смещению и направлена к положению равновесия.

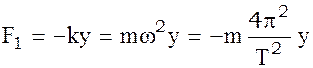(2)

Где 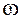– круговая частота и 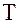– период колебания.

Считая, что при указанных выше ограничениях колебания маятника можно принять за гармонические, приравниваем выражения (1) и (2) и, учитывая, что

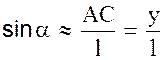(4)

Напишем

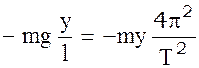(4)

Решая (4) относительно периода колебаний математического маятника, получим:

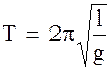(5)

Формула (5) позволяет определить ускорение силы тяжести в данном географическом месте Земли, если известен период колебания математического маятника и его длина.

В лабораторных работах применяется маятник, подвешиваемый на двойной нити для того, чтобы колебания происходили по возможности в одной плоскости. Кроме этого, для устранения необходимости измерять строго сами длины маятников и диаметры шариков, применяют метод измерения двух периодов 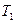и 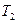при разных длинах маятника

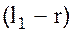и ,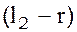

где 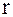– радиус шарика маятника, а 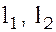– длины подвеса маятников до нижней точки шариков (отсчёты по шкале).

Напишем формулу (5) для этих двух случаев, предварительно возведя в квадрат обе части равенства

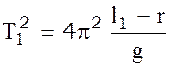(6)

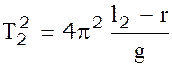(7)

Вычитая почленно (7) из (6), получим:

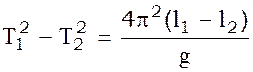(8)

Откуда

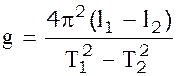(9)

Порядок выполнения работы

1. Устанавливают наибольшую длину мятника и, касаясь подвижной горизонтальной линейкой нижнего края шарика, отмечают число делений на шкале; это соответствует длине .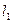

2. Отводя маятник от положения равновесия на небольшой угол (5°-6°), отпускают шарик, предоставив ему возможность свободно колебаться. В момент наибольшего отклонения маятника пускают в ход секундомер и отсчитывают время 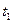, в течение которого маятник совершает n₁ = 50 полных колебаний. Не меняя длины маятника, повторяют опыт пять раз, записывая результаты наблюдений в таблицу.

3. Проделывают аналогично п. 2 измерения и наблюдения при новой длине маятника (l₂ приблизительно на 50 см меньше, чем l₁).

4. Вычисляют периоды колебаний 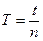для обеих длин маятников и записывают в таблицу. Находят средние значения периодов.

Таблица наблюдений

№№ набл.	l1	t1	n1	T1	<T1>	l2	t2	n2	T1	<T1>	g
Един. измер.	м	с	-	с	с	м	с	-	с	с
1.
2.
3.
4.
5.

5. По формуле (9) для средних периодов вычисляют ускорение силы тяжести.

Контрольные вопросы

1. Дайте определение математического маятника.

2. При каких ограничениях математический маятник совершает гармонические колебания?

3. Что называется гармоническими колебаниями?

4. Дайте вывод формулы периода колебаний математического маятника.

5. Дайте вывод формулы ускорения силы тяжести.

6. От чего зависит величина ускорения силы тяжести?

7. От каких величин зависит период колебания математического маятника? Зависит ли он от массы шарика? Зависит ли он от размеров шарика?

Приложения

Множители и приставки для образования десятичных кратных и дольных единиц и их наименования